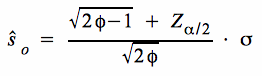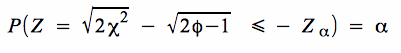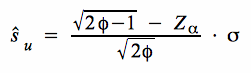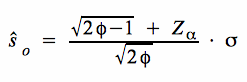| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Konzepte und Definitionen im Modul IV-4 Test der Standardabweichung und der Varianz
Vorbemerkungen
Tests von Hypothesen über die Standardabweichung und die Varianz einer Grundgesamtheit basieren auf der
Stichprobenverteilung der modifizierten Varianz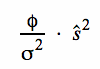 .
Diese ist durch eine
Chi-Quadrat-Verteilung mit φ = n - 1 Freiheitsgraden gegeben.
.
Diese ist durch eine
Chi-Quadrat-Verteilung mit φ = n - 1 Freiheitsgraden gegeben.
Aufgrund der Approximation der Verteilung der durch die Normalverteilung können sich die Testmodelle bei n > 30 auf eine
Normalverteilung mit 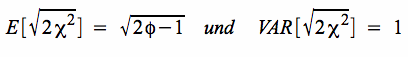 stützen.
stützen.
Voraussetzung für die folgenden Tests ist eine Normalverteilung der Stichprobenvariablen.
-
Die zu testenden Hypothesen können als Punkthypothese bzw. als Bereichshypothesen formuliert werden. Letztere führen dann wieder zu links- oder rechtsseitigen Tests.
Wie bereits bei den Tests von Hypothesen bezüglich des Mittelwertes und des Anteilswertes stehen auch für die hier vorgestellten Tests äquivalente Ansätze zur Verfügung.
Annahme- und Ablehnungsbereiche können sowohl für
-
die Ausgangsgrößen (Varianzen und Standardabweichungen), wie für
die daraus abgeleiteten Größen χ² bzw. Z (nach einer Approximation) definiert werden.
Tests auf der Basis eines Vergleich der Wahrscheinlichkeiten α und α0 sind aufgrund der nur für bestimmte Wahrscheinlichkeiten tabellierten Werte ohne Verteilungsrechner nicht durchführbar .
Im Folgenden betrachten wir zuerst Hypothesentests auf der Basis n ≤ 30.
1. Hypothesentests auf der Basis n ≤ 30
-
Tests unter dieser Voraussetzung stützen sich auf die nicht-symmetrische Chi-Quadrat-Verteilung, woraus bei beidseitigen Tests nicht-symmetrische Randbereiche resultieren.
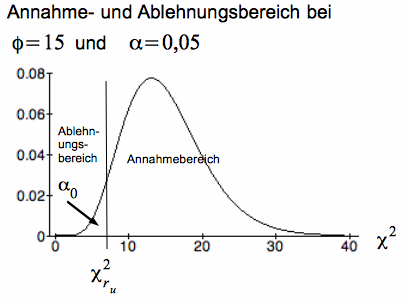
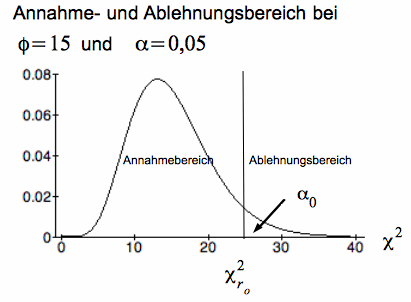
Im konkreten Fall erhalten wir die Grenzwerte für χ² bei gegebenen Freiheitsgraden φ = n - 1 und dem Signifikanzniveau aus der Tabelle der Chi-Quadrat-Verteilung. Es gilt dabei:
χ²ru = χ²(1 - α0/2) bzw. χ²(1 - α0) und
χ²ro = χ²α0/2 bzw. χ²α0
Eine Tabelle für χ²
finden Sie in der Tabellenübersicht
.
-
Die Grenzen der Annahme-/ Ablehnungsbereiche für Testmodelle auf der Grundlage von ŝ lassen sich durch Auflösung von 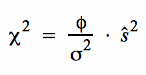 nach ŝ bestimmen.
nach ŝ bestimmen.
a. Testmodell für H 0: σ = σ 0
Bei der Berechnung der Zurückweisungspunkte erhalten wir für die obige Hypothese einen beidseitigen Test :
|
|
Abb. IV-15 beidseitiger Test

|
b. Testmodell für H 0: σ ≥ σ 0
Bei der Berechnung des Zurückweisungspunktes erhalten wir für die obige Hypothese einen linksseitigen Test:
|
|
Abb. IV-16 linksseitiger Test
|
c. Testmodell für H 0: σ ≤ σ 0
Bei der Berechnung des Zurückweisungspunktes erhalten wir für die obige Hypothese einen rechtsseitigen Test :
|
|
Abb. IV-17 rechtsseitiger Test
|
2. Hypothesentests auf der Basis n > 30
a. Testmodell für H 0: σ = σ 0
Bei der Berechnung der Zurückweisungspunkte erhalten wir für die obige Hypothese
b. Testmodell für H 0: σ ≥ σ 0
Bei der Berechnung des Zurückweisungspunktes erhalten wir für die obige Hypothese
c. Testmodell für H 0: σ ≤ σ 0
Bei der Berechnung des Zurückweisungspunktes erhalten wir für die obige Hypothese
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel03_Hypothesentests/modul01x15_Test~~lder~~lStandardabweichung~~lund~~lder~~lVarianz/ebene01_Konzepte~~lund~~
lDefinitionen/03__01x15__01__01.php3
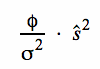 .
Diese ist durch eine
Chi-Quadrat-Verteilung mit φ = n - 1 Freiheitsgraden gegeben.
.
Diese ist durch eine
Chi-Quadrat-Verteilung mit φ = n - 1 Freiheitsgraden gegeben.
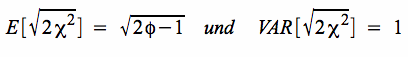 stützen.
stützen. 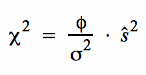 nach ŝ bestimmen.
nach ŝ bestimmen.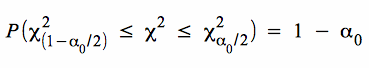 angenommen, wenn
angenommen, wenn 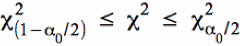 .
.
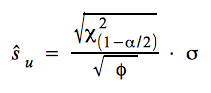
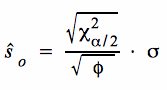


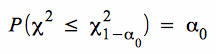 abgelehnt, wenn
abgelehnt, wenn 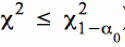 .
.
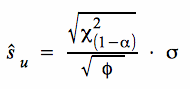

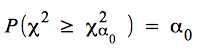 abgelehnt, wenn
abgelehnt, wenn 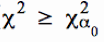 .
. 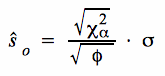

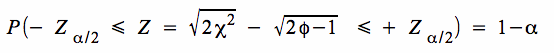
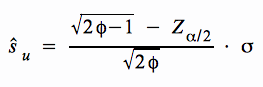 und
und