 |
Konzepte und Definitionen im Modul II-2 Die Normalverteilung
1. Vorbemerkung
Die Normalverteilung stellt die wichtigste
theoretische Verteilung in der induktiven Statistik dar. Sie wurde von C.F.Gauß zur formelhaften Beschreibung von Körpermaßen preussischer Rekruten entwickelt.
Empirisch ergibt sich eine Normalverteilung
in der Regel dann, wenn eine Zufallsvariable mit sehr vielen
Merkmalsausprägungen von sehr vielen Zufallsfaktoren abhängt.
Die Form der
Normalverteilung hängt lediglich von zwei Parametern ab, nämlich
der Standardabweichung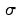 und
dem Mittelwert .
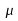Dies ist für die praktische Arbeit natürlich besonders
vorteilhaft.
2. Die Standardnormalverteilung und ihre Eigenschaften
Eine Normalverteilung mit der Standardabweichung
σ = 1 und
dem Mittelwert μ = 0 bezeichnet
man als Standardnormalverteilung. Zur Unterscheidung von
Normalverteilungen mit beliebigen Parameterwerten wird die
Standardnormalvariable mit dem Symbol Z charakterisiert.
Die Kurzbezeichnung für die Standardnormalverteilung bezieht sich auf die Werte ihrer Parameter und lautet N (0,1).
a) Die Dichtefunktion der Standardnormalverteilung
Die Formel für die Dichtefunktion
lautet:
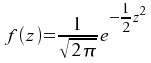
Die graphische Darstellung der
Dichtefunktion ergibt die sog. Glockenkurve :
Abbildung II-3: Dichtefunktion der
Standardnormalverteilung
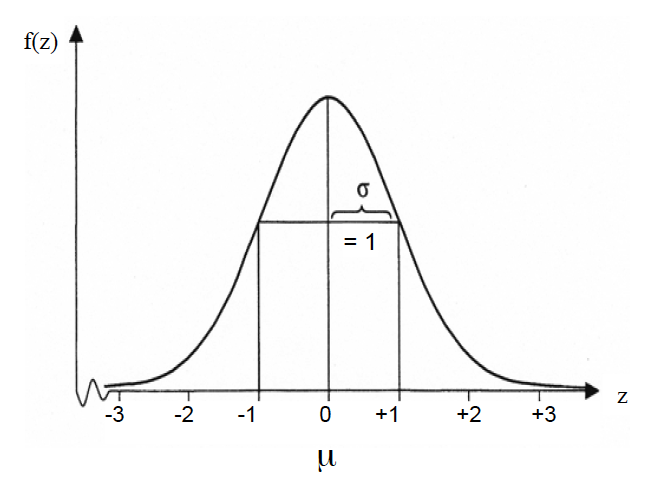
Die Funktionsmerkmale
Die Funktion ist symmetrisch,
sie erstreckt sich über den Bereich 0 ± ∞,
sie hat ihr Maximum bei z = 0, d.h. bei μ,
sie besitzt Wendepunkte bei z = ± 1, d.h. bei ± σ ,
da es sich um eine Dichtefunktion handelt, hat die Fläche unter der Funktion den Wert 1,
es gilt P( z < 0 = μ) = 0,5.
Die Berechnung der Werte der Dichtefunktion
Da die Berechnung einzelner Dichtewerte sehr
aufwendig ist, werden für die manuelle Arbeit, wie schon im
Falle der Binomialverteilung, tabellierte Werte herangezogen. Allerdings sind für die Durchführung der Hypothesentests und der Konfidenzschätzungen die Werte der Verteilungsfunktion maßgeblich.
Tabelle II-2: Tabelle der Dichtefunktion der
Standardnormalverteilung
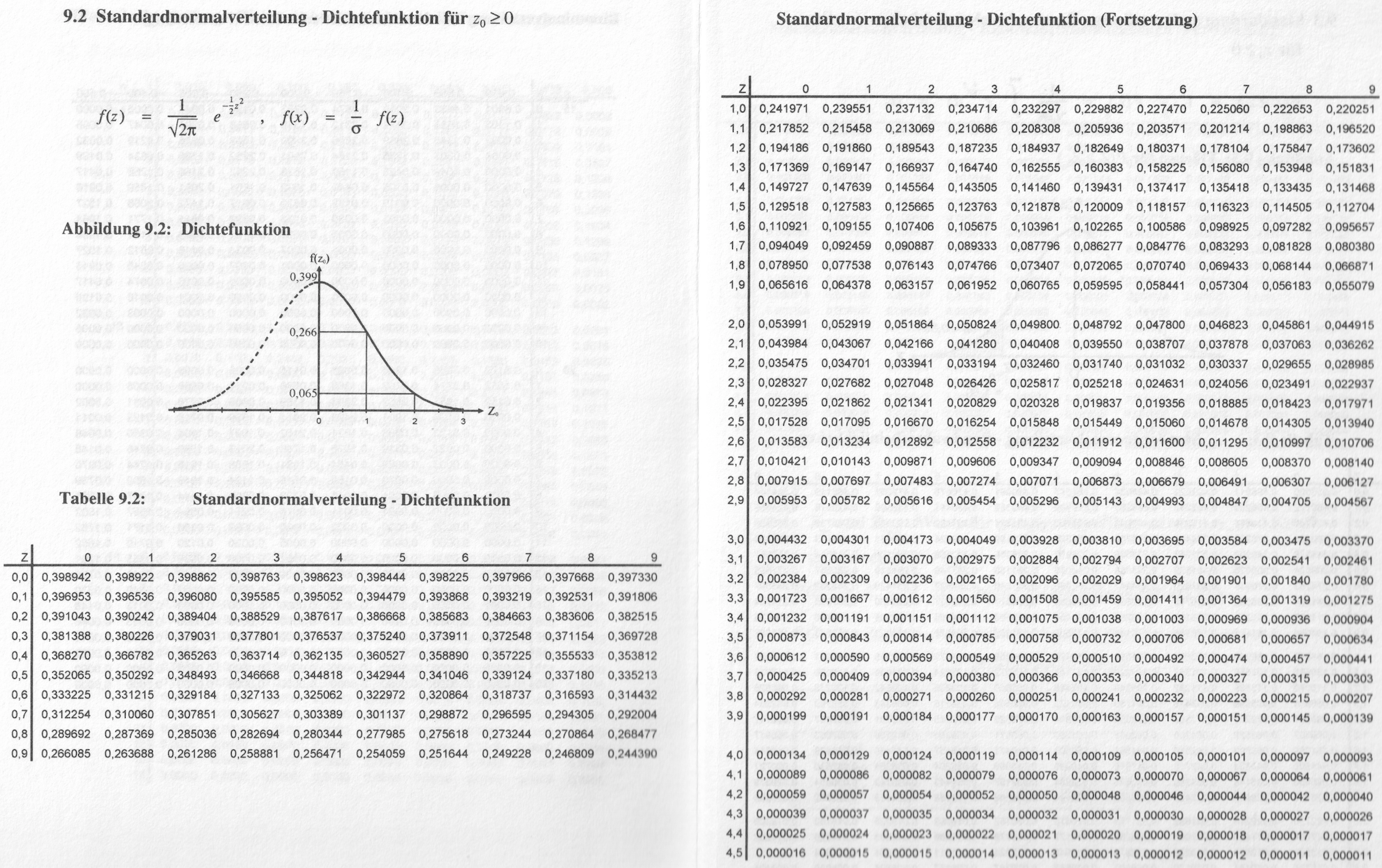
Quelle: Litz: Statistische Methoden in den Wirtschafts- und Sozialwissenschaften, 3. Auflage, München 2001, S.384 f.
b) Die Verteilungsfunktion der Standardnormalverteilung
Von größerer
praktischer Bedeutung als die Dichtefunktion ist jedoch die
Verteilungsfunktion der Standardnormalverteilung, die die
Wahrscheinlichkeit angibt, dass die Z - Werte Z ≤ z 0 annehmen:
Die Formel für die Verteilungsfunktion
lautet:
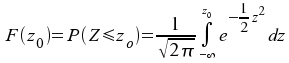
Die graphische Darstellung der
Verteilungsfunktion ergibt die folgendes Bild:
Abbildung II-4: Verteilungsfunktion der
Standardnormalverteilung
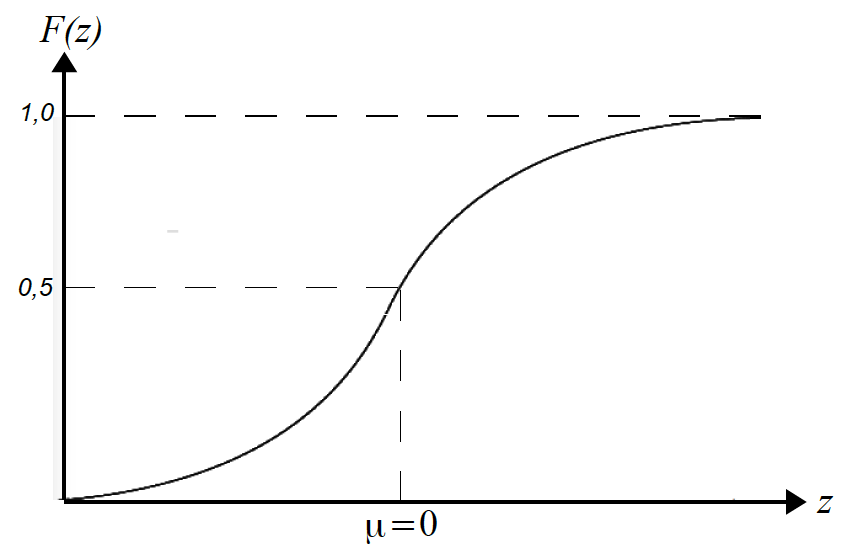
Zur Charakterisierung der Funktion lässt sich festhalten:
Die Funktion besitzt bei z = 0, d.h. bei μ einen Wendepunkt,
Die Funktion nähert sich bei z > 3 asymptotisch dem Wert 1.
c) Die Tabellierung der Verteilungsfunktion
Bei der Arbeit mit der Tabelle ist zu beachten, dass häufig (wie auch im Folgenden) aus
praktischen Gründen statt F(z 0) der
Wert von 1 - F(z 0) tabelliert
wird, also die Wahrscheinlichkeit, dass Z einen Wert Z ≥ z 0 annimmt.
Wegen der Symmetrie der Normalverteilung gilt zudem P(Z ≥ +z 0) = P(Z ≤ -z 0).
Tab. II-3 präsentiert auszugsweise die Randwahrscheinlichkeiten
für 0 ≤ z 0 ≤ 1,59:
Tabelle II-3: Wahrscheinlichkeiten der
Standardnormalverteilung P(Z ≥ +z 0) (für 0 ≤ z 0 ≤ 1,59)
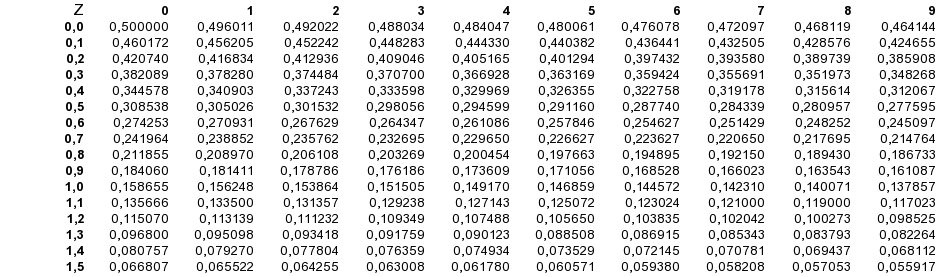
In der Tabelle sind in der Vorspalte die ersten beiden Ziffern
des z0 -Wertes,
in der Überschriftenzeile die 3. Ziffer (2. Nachkommastelle)
notiert. Im Tabellenkörper findet sich der Wert für P(Z ≥ +z 0). So beträgt z. B. die Wahrscheinlichkeit für Z ≥ 1.33 etwa 0.092.
Eine ausführliche Tabelle der Wahrscheinlichkeiten F(Z ≥ 1.5) = α finden Sie hier.
d) Die Ermittlung der Randwahrscheinlichkeiten
Für die Operationen der schließenden Statistik, die Hypothesentests und Konfidenzschätzungen, sind die Randwahrscheinlichkeiten der Verteilungsfunktion der Standardnormalverteilung von zentraler
praktischen Bedeutung.
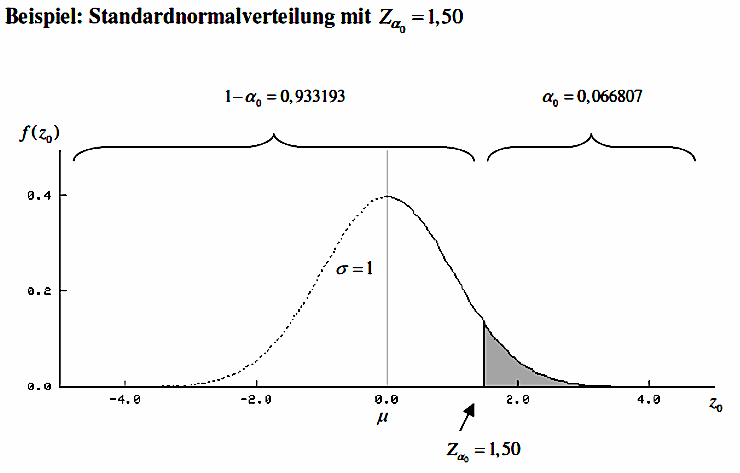
In der folgenden Graphik der Dichtefunktion sind für einen z-Wert von 1.5 die Wahrscheinlichkeiten F(Z ≤ 1.5) = 1 - α = 0.933193 und die tabellierte Wahrscheinlichkeit F(Z ≥ 1.5) = α = 0.066807 (vgl. Tab. II-2. letzte Zeile erste Spalte) dargestellt.
Abbildung II-5: Randwahrscheinlichkeiten
Im Internet finden sich eine Reihe von applets, mit denen man beliebige Normalverteilungen graphisch darstellen und beliebige Wahrscheinlichkeiten der Normalverteilung berechnen kann.
unter diesem externen Link der Universität in Iowa.
Ein weiterer Rechner zur Bestimmung beliebiger Wahrscheinlichkeiten findet sich unter diesem externen Link .
Eine grafische Darstellung der Normal-Verteilung liefert auch der
Verteilung-Plotter von N. Johnston .
Eine weitere Alternative findet sich hier.
3. Die Normalverteilung und ihre Eigenschaften
In der Regel arbeiten wir mit
Normalverteilungen, die ein beliebiges μ und σ aufweisen.
Die Kurzbezeichnung für die Normalverteilung bezieht sich auf die Werte ihrer Parameter und lautet N (μ,σ).
a) Die Dichtefunktion der Normalverteilung
Für diese generelle Form der Dichtefunktion gilt die Formel:
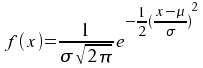
Ihre graphische Darstellung ist in Abb. II-6 wiedergegeben:
Abbildung II-6: Dichtefunktion einer
Normalverteilung mit μ 400 und σ = 100
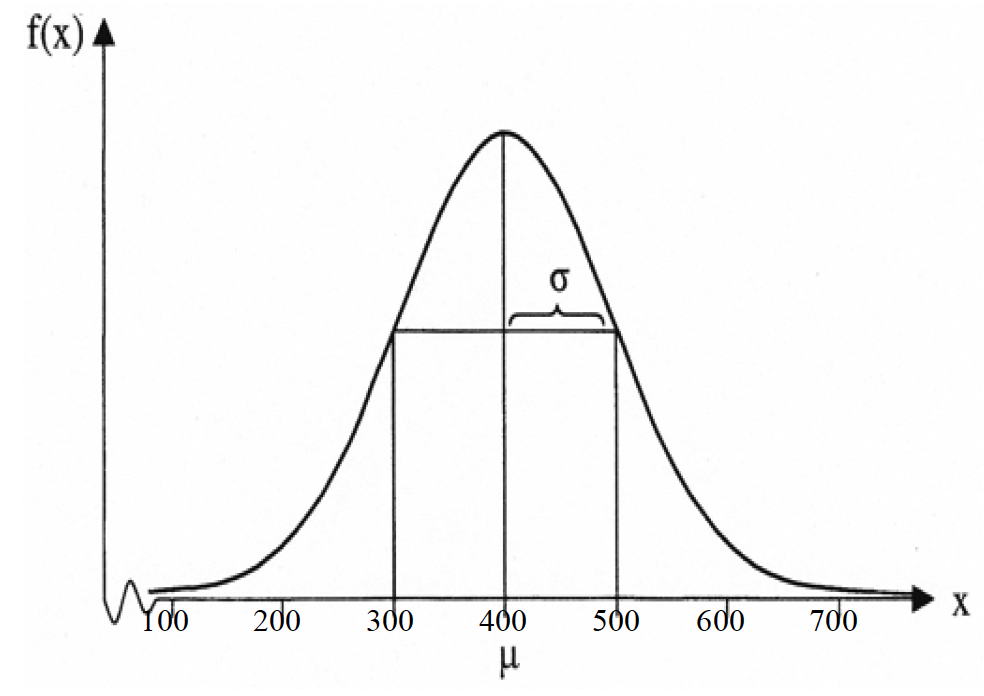
Die Charakterisierung der Funktion ergibt analog zu der der Standardnormalverteilung
Die Funktion ist symmetrisch,
sie erstreckt sich über den Bereich μ ± ∞,
sie hat ihr Maximum bei x = μ,
sie besitzt Wendepunkte bei μ ± σ ,
da es sich um eine Dichtefunktion handelt, hat die Fläche unter der Funktion den Wert 1,
es gilt P(x < μ) = 0,5.
b) Die σ-Intervalle
Aus der Form der Normalverteilung ergibt sich eine
weitere wichtige Eigenschaft:
Unabhängig von Mittelwert und Standardabweichung
ist immer ein bestimmter Teil der Gesamtfläche in symmetrischen
Intervallen +/- einem Vielfachen der Standardabweichung um den
Mittelwert zu finden.
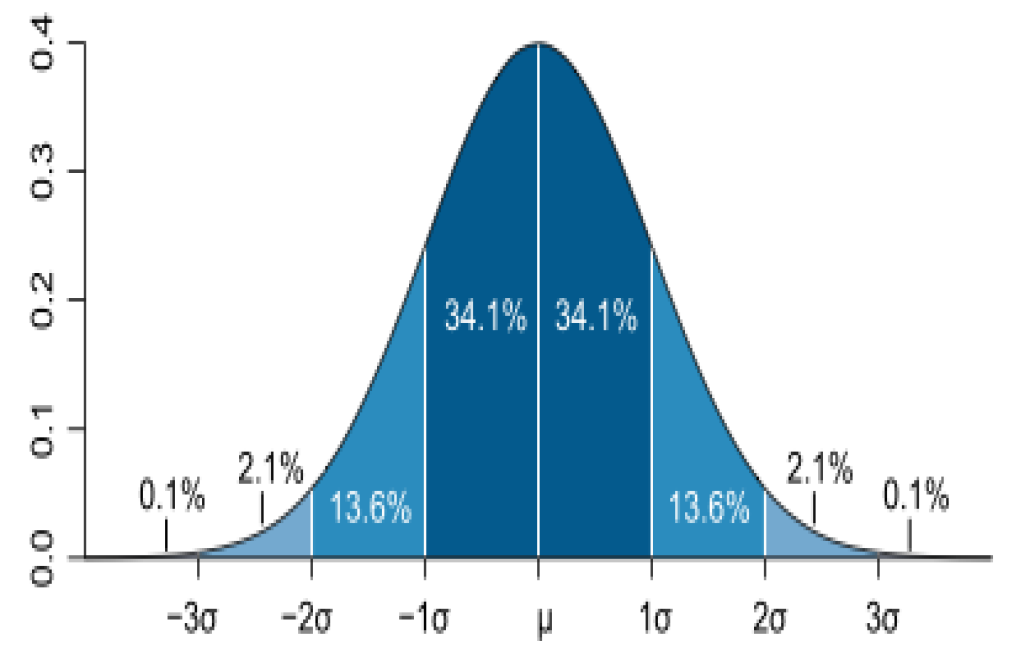
Das Intervall μ ± 1 · σ enthält etwa 68% der Gesamtfläche,
das Intervall μ ± 2 · σ enthält etwa 95% und
das Intervall μ ± 3 · σ enthält etwa 99% der Gesamtfläche (vgl. Abb. II-7)
Abbildung II-7:
k · σ-
Bereiche unter der Normalverteilung (k=1,2,3)
Dieser Zusammenhang zwischen Fläche und
Standardabweichung kann zur Transformation beliebiger
Normalverteilungen in die Standardnormalverteilung genutzt werden.
c) Die Standardisierung beliebiger
Normalverteilungen
Sinn und Zweck der Standardisierung
Das Verfahren, beliebige Normalverteilungen zu
standardisieren, d.h. in eine Standardnormalverteilung zu
transformieren, umgeht auf einfache Art und Weise eine manuelle
Berechnung der Verteilungsfunktionen beliebiger Normalverteilungen.
Da die Verteilungs- und Dichtefunktion der Standardnormalverteilung
tabelliert vorliegt, kann auf sie zurückgegriffen werden.
Bei dieser sog. Z-Transformation werden
die Abweichungen eines beliebigen normalverteilten Variablenwertes
von seinem Erwartungswert μ in
einem Vielfachen der Standardabweichung σ ausgedrückt:
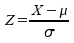
Bestimmung der Randwahrscheinlichkeiten
Es gilt dabei für gegebene x0:
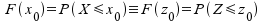
Der Vorteil der Z-Transformation liegt auf der Hand:
Soll die Fläche eines Segmentes unter einer beliebigen
Normalverteilung ermittelt werden, so müssen nur die Grenzen a
und b dieses Intervalls in z-Werte transformiert werden.
Anschließend
kann die Wahrscheinlichkeit P( a ≥ X ≥ b) als P( za ≥ Z ≥ zb ) aus
den tabellierten Werten der Verteilungsfunktion der
Standardnormalverteilung ermittelt werden.
-
Übersicht II-1:
Aspekte der Z-Transformation
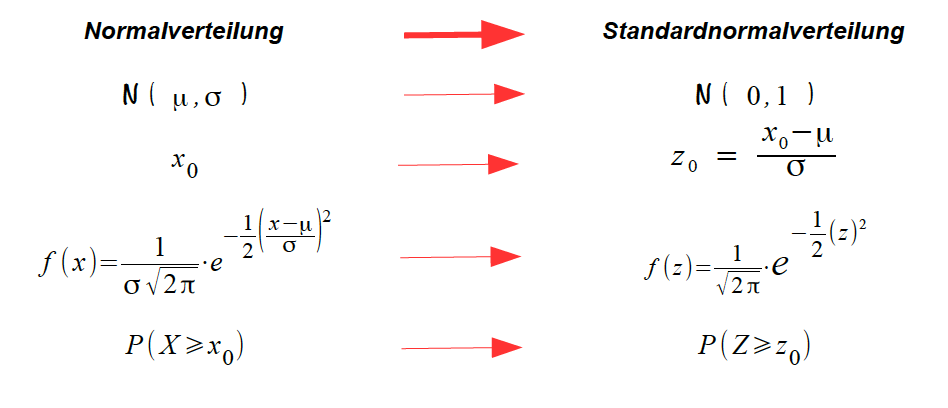
Zur Praxis der Z-Transformation
Welche Fragestellungen können nun mit Hilfe einer Z-Transformation bearbeitet werden? Dazu gibt es zwei Varianten, die am Beispiel von IQ-Tests erläuter werden sollen.
IQ-Tests sind i.d.R. auf einen Mittelwert von 100 und eine Standadabweichung von 15 kalibriert, ihre Ergebnisse sind in etwa normalverteilt.
Zwei Fragestellungen liegen auf der Hand:
Wie wahrscheinlich ist ein IQ von mindestens, sagen wir 130? oder umgekehrt:
Wie hoch ist der IQ der 10% intelligentesten Mitbürger?
Zur Bearbeitung dieser Fragestellungen benötigen wir die Informationen aus der hier abzurufenden Tabelle.
Die Wahrscheinlichkeit eines IQ ≥ 130
Gesucht ist hier: P(X ≥ 130)?
Dieses erste, in den Grundzügen bereits thematisiertes Problem, erfordert die Umrechnung von x0 = 130 in z0 über 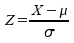. Wir erhalten hier konkret: z0 = (130 - 100)/ 15 = 2.
In der verlinkten Tabelle finden wir für z0 ≥ 2,00 über den Wert 2,0 in der Vorspalte und den Wert 0 in der 1. Zeile im Tabellenfeld eine Wahrscheinlichkeit von 0,02275, also etwa von 2,3 %.
Der Mindest-IQ der 10% intelligentesten Personen
Die Bearbeitung der zweiten Fragestellung basiert ebenfalls auf der Z-Transformation 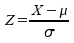erfordert aber die Auflösung der Formel nach x0 .
Daraus resultiert die wichtige Beziehung:
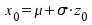
Für diese Formel müssen wir (u.U. nach Interpolation) den Wert für z0 ermitteln, der der Wahrscheinlichkeit von 0,10 entspricht. In der Tabelle kann eine Wahrscheinlichkeit von 0,10023 als hinreichend genaue Annäherung an die vorgegegben %-Zahl genommen werden, sodass wir das zugeordneten z0 = 1,28 in die Formel einsetzen können.
Wir erhalten so: x0 = 100 + 15 · 1,28 = 119,2. D.H. also, dass die 10% intelligentesten Personen mindestens einen IQ von 119,2 aufweisen müssen.
|
