 |
Konzepte und Definitionen im Modul III-2 Stichprobenverteilungen der modifizierten Standardabweichungen
1. Die Stichprobenverteilung der modifizierten Varianz ŝ²
a) Die Definition der Prüfgröße
b) Die Stichprobenverteilung der Prüfgröße
Diese
Prüfgröße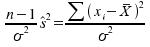 ist annähernd ist annähernd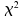 -verteilt
mit n-1 Freiheitsgraden. -verteilt
mit n-1 Freiheitsgraden.
Für
Stichproben aus einer normalverteilten Grundgesamtheit, können
wir deshalb bei 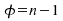 schreiben: schreiben:
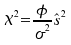
Abbildung III-8: Stichprobenverteilung der Prüfgröße bei φ = 8
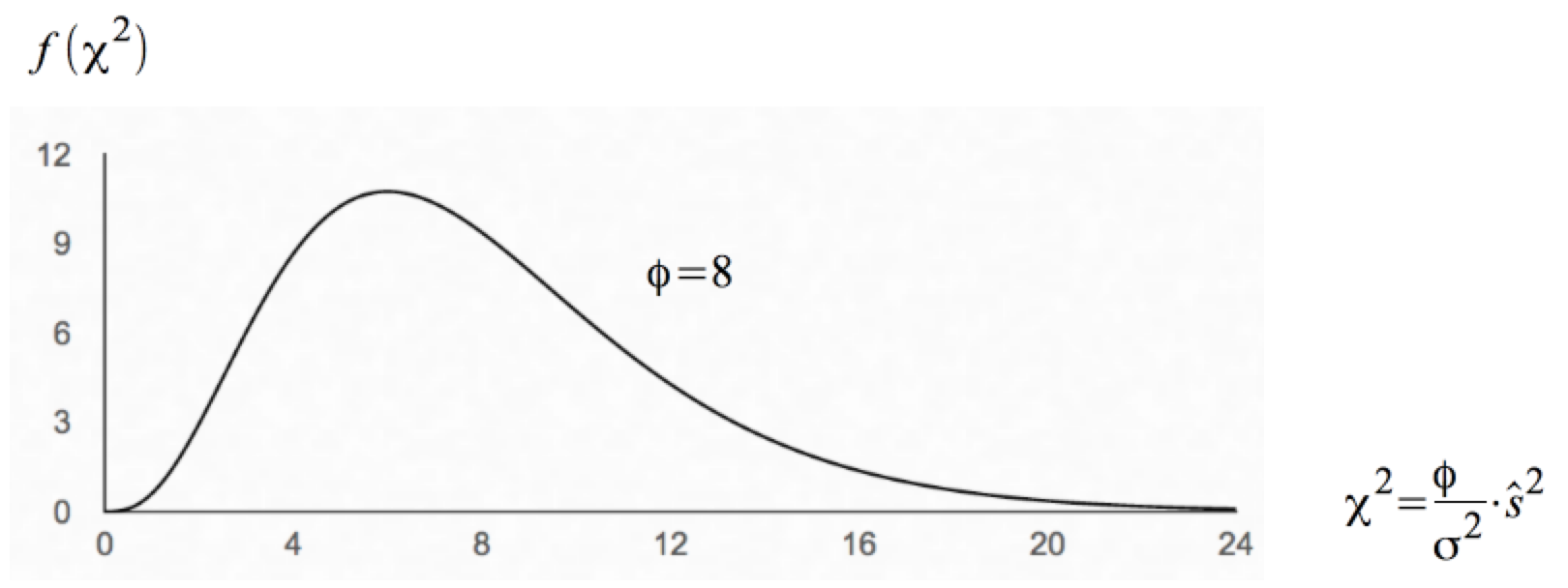
2. Die Abschätzungen eines Intervalls für die Standardabweichung ŝ
a) Die Definition des Intervalls
b) Die Grenzen des Intervalls
Da die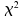 -Verteilung
nicht symmetrisch ist, ergeben sich hierbei, anders als im Falle der
Standardnormalverteilung zwei unterschiedliche Werte. Wir erhalten: -Verteilung
nicht symmetrisch ist, ergeben sich hierbei, anders als im Falle der
Standardnormalverteilung zwei unterschiedliche Werte. Wir erhalten:
für die
untere Grenze:
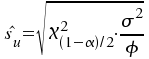
3. Die Approximation der χ²-Verteilung durch die Standardnormalverteilung
a) Die Definition der standardnormalverteilten Prüfgröße
Zuerst nehmen wir eine
Approximation an die Normalverteilung vor:
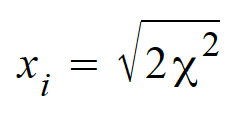 ist
annähernd normalverteilt mit dem Erwartungswert ist
annähernd normalverteilt mit dem Erwartungswert
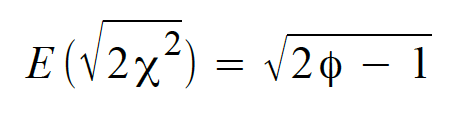 und
der Varianz und
der Varianz 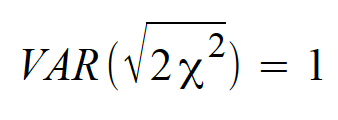 . .
Für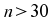 ergibt
sich daraus die standardnormal-verteilte Prüfgröße: ergibt
sich daraus die standardnormal-verteilte Prüfgröße:
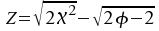 mit mit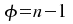 . .
b) Die Grenzen des Intervalls 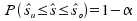
Daraus folgt durch Einsetzen von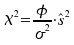 und
Auflösen nach und
Auflösen nach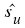 und und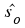 : :
|



