 |
Konzepte und Definitionen im Modul II-3 Die Chi-Quadrat-Verteilung
1. Vorbemerkungen
Die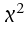 -Verteilung
dient in der induktiven Statistik als Basis der Verteilung von
Stichprobenvarianzen und -standardabweichungen und ist somit
Grundlage der statistischen Schlüsse auf die entsprechenden
Parameter der Grundgesamtheit. -Verteilung
dient in der induktiven Statistik als Basis der Verteilung von
Stichprobenvarianzen und -standardabweichungen und ist somit
Grundlage der statistischen Schlüsse auf die entsprechenden
Parameter der Grundgesamtheit.
Darüber hinaus erlaubt
die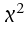 -Verteilung
eine wahrscheinlichkeitstheoretische Beurteilung der deskriptiven
Kontingenzmaße. -Verteilung
eine wahrscheinlichkeitstheoretische Beurteilung der deskriptiven
Kontingenzmaße.
Die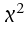 -Verteilung
ist für n > 30 durch die Normalverteilung approximierbar. -Verteilung
ist für n > 30 durch die Normalverteilung approximierbar.
2. Die Chi-Quadrat-Funktion und ihre Eigenschaften
a) Die Dichtefunktion
b) Die Parameter und Maßzahlen der Dichtefunktion
c) Die graphische Darstellung der Dichtefunktion
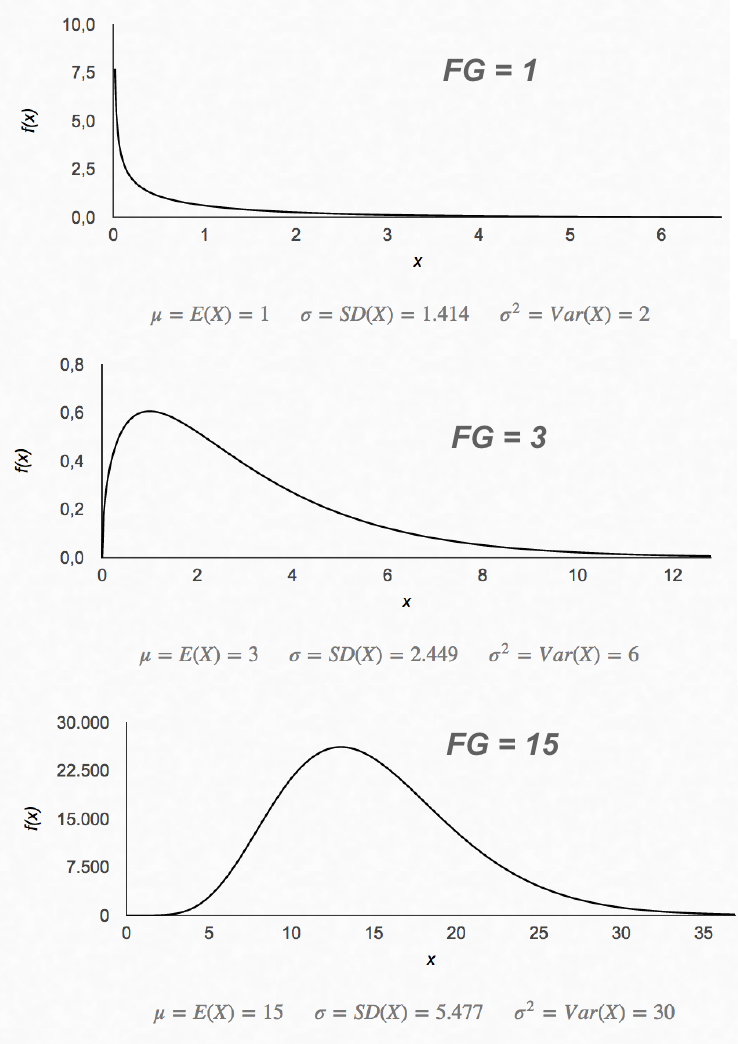
Die Graphen der
Dichtefunktionen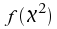 sind
für sind
für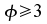 unimodal
und werden mit steigenden Freiheitsgraden zunehmend symmetrisch. unimodal
und werden mit steigenden Freiheitsgraden zunehmend symmetrisch.
Abbildung II-11: χ 2-Verteilung
für φ = 1, 3 u. 15
 hier und hier .
hier und hier .
d) Die tabellierte Verteilungsfunktion
Wie für die Normalverteilung liegen die Wahrscheinlichkeiten
der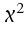 -Verteilung
für Werte der Verteilungsfunktion von -Verteilung
für Werte der Verteilungsfunktion von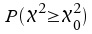 in
tabellierter Form vor. Diese werden auszugsweise für in
tabellierter Form vor. Diese werden auszugsweise für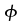 = 1...15 in
Tab. II-5 widergegeben. Dabei sind die Freiheitsgrade in der
Vorspalte der Tabelle zu finden, die kritischen Werte für = 1...15 in
Tab. II-5 widergegeben. Dabei sind die Freiheitsgrade in der
Vorspalte der Tabelle zu finden, die kritischen Werte für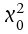 im
inneren der Tabelle und die korrespondierenden Wahrscheinlichkeiten
in den Spaltenüberschriften. im
inneren der Tabelle und die korrespondierenden Wahrscheinlichkeiten
in den Spaltenüberschriften.
Tabelle II-5:
Tabellierte
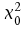 -Werte
für -Werte
für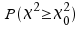 und und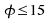
Eine ausführliche Tabelle für φ ≤ 40 findet sich hier.
-
Ein Rechner
zur Berechnungg von Wahrscheinlichkeiten für beliebige Freiheitsgrade findet sich ausserdem unter diesem externen Link.
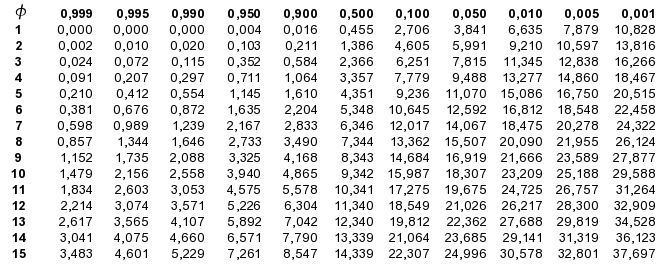
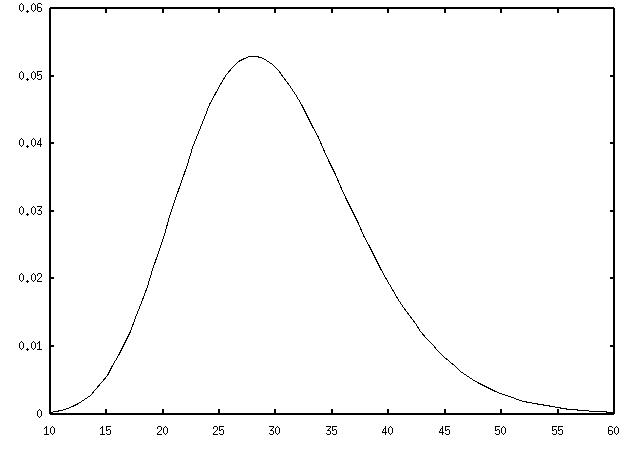
d) Die Approximation durch die Normalverteilung
Ab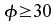 kann
die kann
die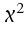 -Verteilung
durch die Normalverteilung approximiert werden. Wie die Abbildung II-12 zeigt, lässt die Symmetrie allerdings noch zu wünschen
übrig. -Verteilung
durch die Normalverteilung approximiert werden. Wie die Abbildung II-12 zeigt, lässt die Symmetrie allerdings noch zu wünschen
übrig.
Abbildung II-12: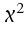 -Verteilung
für -Verteilung
für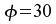
Aus diesem Grunde ist eine indirekte
Approximation an die Normalverteilung über
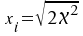 vorzuziehen
ist. vorzuziehen
ist.
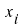 ist
annähernd normalverteilt mit dem Erwartungswert ist
annähernd normalverteilt mit dem Erwartungswert
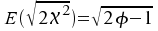 und
einer Varianz von Eins. und
einer Varianz von Eins.
Daraus resultiert folgende Standard-Normalvariable:
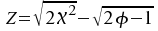
|



