 |
Konzepte und Definitionen im Modul IV-5 Chi-Quadrat-Tests
Vorbemerkungen
Unter dem Begriff der Chi-Quadrat-Tests werden zwei unterschiedliche Testkonzepte auf der Grundlage einer
Chi-Quadrat-Verteilung subsummiert, deren Kern im Vergleich einer empirischen Häufigkeit mit einer theoretischen Häufigkeit besteht.
Der 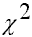 -Unabhängigkeitstest prüft, ob eine gegebene zweidimensionale Häufigkeitsverteilung der Variablen Xi und Yi aus einer Grundgesamtheit stammen kann, in der Xi und Yi unabhängig voneinander verteilt sind. Diese Fragestellung ist aus der deskriptiven Statistik als Kontingenzanalyse bekannt. -Unabhängigkeitstest prüft, ob eine gegebene zweidimensionale Häufigkeitsverteilung der Variablen Xi und Yi aus einer Grundgesamtheit stammen kann, in der Xi und Yi unabhängig voneinander verteilt sind. Diese Fragestellung ist aus der deskriptiven Statistik als Kontingenzanalyse bekannt.
Der 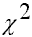 -Anpassungstest prüft, ob eine empirisch gegebene Häufigkeitsverteilung durch eine bestimmte theoretische Verteilung zu beschreiben ist. So kann z.B. überprüft werden, ob die Augenzahlen eines Würfels gleichverteilt sind oder ob ein konkretes empirisches Merkmal in der Grundgesamtheit normalverteilt ist. -Anpassungstest prüft, ob eine empirisch gegebene Häufigkeitsverteilung durch eine bestimmte theoretische Verteilung zu beschreiben ist. So kann z.B. überprüft werden, ob die Augenzahlen eines Würfels gleichverteilt sind oder ob ein konkretes empirisches Merkmal in der Grundgesamtheit normalverteilt ist.
In beiden Fällen lautet die Nullhypothese: 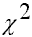 = 0, d.h. dass die Unterschiede jeweils nur zufällig sind. = 0, d.h. dass die Unterschiede jeweils nur zufällig sind.
Sowohl der Anpassungs- wie auch der Unabhängigkeitstest sind somit rechtsseitige Tests.
1. Der Chi-Quadrat-Unabhängigkeitstest
a) Ausgangspunkt: Die Kontingenzanalyse
Der 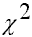 -Unabhängigkeitstest prüft, ob zwei Variablen Xi und Yi in der Grundgesamtheit unabhängig voneinander verteilt sind. -Unabhängigkeitstest prüft, ob zwei Variablen Xi und Yi in der Grundgesamtheit unabhängig voneinander verteilt sind.
Die dem Test zugrunde liegende Formel entspricht dem aus der Kontingenzanalyse bekanntem Algorithmus.
Er lautet:
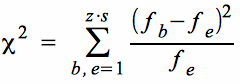
wobei fb die beobachtete und fe die erwartete Häufigkeit ist. Summiert wird über die Anzahl der z · s Tabellenfelder.
Voraussetzung dafür, dass die so berechnete Größe tatsächlich einer χ²-Verteilung folgt, ist: fe ≥ 5. Ist diese Voraussetzung nicht gegeben, müssen die Zeilen oder Spalten der Kontingenztabelle zusammengefasst werden.
b) Die Ermittlung der Werte
Die beobachteten Werte sind mit den Felderwerten einer zwei- oder mehrdimensionalen Kontingenztabelle gegeben.
Tab.: IV-3: Kontingenztabelle, Erwerbstätigkeit nach Geschlecht 
-
Die erwarteten Häufigkeiten sind der Indifferenztabelle zu entnehmen. Deren Werte müssen aus den Randverteilungen der Kontingenztabelle berechnet werden.
Tab.: IV- 4: Indifferenztabelle, bei Unabhängigkeit erwartete Häufigkeiten
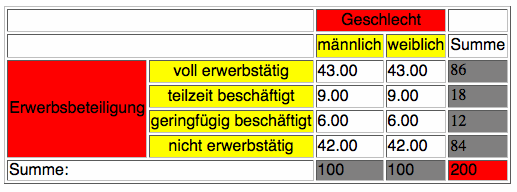
Die Konstruktion der Indifferenztabelle erfolgt über den Satz 4 der Statistischen Unabhängigkeit:

Für f1,1 ergibt sich: f1,1 = (86 · 100)/ 200 = 43.
-
Die Freiheitsgrade berechnen sich über: 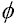 = (z-1) · (s-1); hier: (4 - 1)(2 - 1) = 3 = (z-1) · (s-1); hier: (4 - 1)(2 - 1) = 3
c) Der Test auf Unabhängigkeit
Die zu testende Hypothesen lautet: H0: 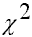 = 0, d.h. die Kontingenztabelle stellt eine Stichprobe aus einer Grundgesamtheit dar, in der die beiden Variablen unabhängig sind. = 0, d.h. die Kontingenztabelle stellt eine Stichprobe aus einer Grundgesamtheit dar, in der die beiden Variablen unabhängig sind.
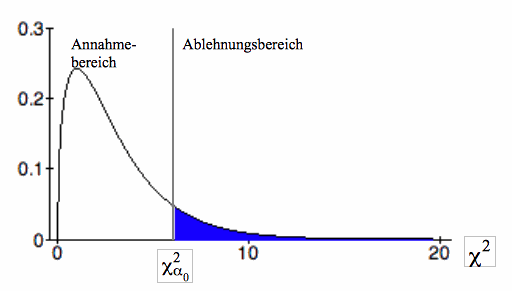
Diese Hypothese ist anzunehmen, wenn der empirische χ²-Wert  in den Annahmebereich fällt (vgl. Abb. IV-19). in den Annahmebereich fällt (vgl. Abb. IV-19). Abb.: IV- 19: Annahme- und Ablehnungsbereich bei 3 Freiheitsgraden und einem Signifikanzniveau von 0,1
2. Der Chi-Quadrat-Anpassungstest
a) Ausgangspunkt: Die empirische Häufigkeitsverteilung
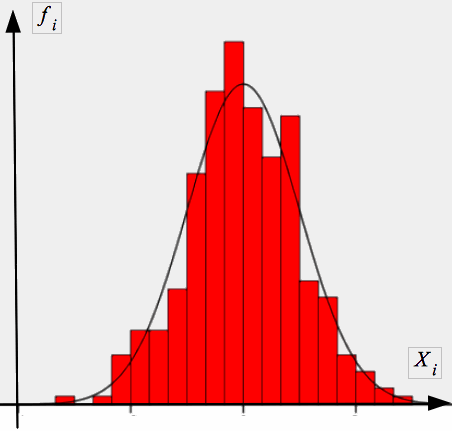
Der  -Anpassungstest prüft, ob eine gegebene, klassierte Häufigkeitsverteilung durch eine bestimmte theoretische Verteilung zu beschreiben ist. So kann, wie bereits erwähnt, getestet werden, ob die Augenzahlen eines Würfels gleichverteilt sind (vgl. Abb. IV-20) oder ob ein konkretes empirisches Merkmal in der Grundgesamtheit normalverteilt ist (vgl. Abb. IV-21). -Anpassungstest prüft, ob eine gegebene, klassierte Häufigkeitsverteilung durch eine bestimmte theoretische Verteilung zu beschreiben ist. So kann, wie bereits erwähnt, getestet werden, ob die Augenzahlen eines Würfels gleichverteilt sind (vgl. Abb. IV-20) oder ob ein konkretes empirisches Merkmal in der Grundgesamtheit normalverteilt ist (vgl. Abb. IV-21).
Abb. IV-20: Häufigkeiten von Augenzahlen beim Würfelwurf 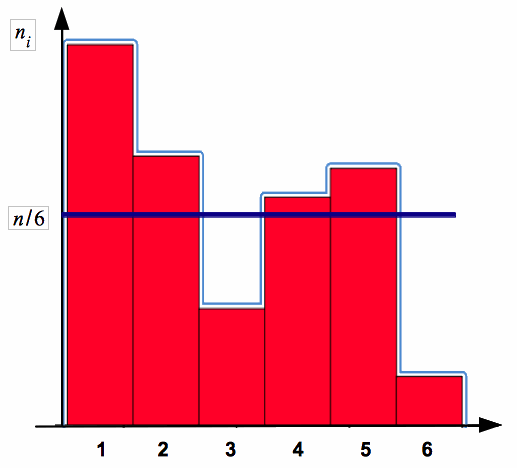
Abb. IV-21: Anpassung einer empirischen Verteilung an eine Normalverteilung
b) Die Ermittlung der Werte
Die dem Anpassungstest zu Grunde liegende Formel für 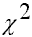 lautet: lautet:
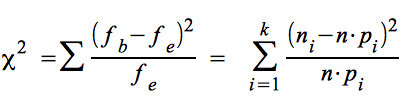
Summiert wird über die Anzahl der Klassen.
Voraussetzung dafür, dass die so berechnete Größe tatsächlich einer χ²-Verteilung folgt, ist die Bedingung: n · pi ≥ 5. Ist diese Voraussetzung nicht gegeben, müssen die Zellen der empirischen Tabelle zusammengefasst werden.
Die χ²-Formel bezieht sich somit
einerseits auf die
empirisch beobachteten absoluten Häufigkeiten fi = ni einer in k Klassen klassierte Variable Xi (i = 1...k), andererseits auf
die, entsprechend einer theoretischen Verteilung für die Xi zu erwartenden absoluten Häufigkeiten n · pi .
Für eine diskrete Zufallsvariable Xi ergibt sich die Wahrscheinlichkeit pi aus der entsprechenden Formel bzw. Tabelle (etwa bei einer Binomialverteilung). Sie ist im Würfelbeispiel bei Gleichverteilung mit pi = 1/6 apriori gegeben.
-
Für eine klassierte stetige Variable Xi muss sie aufwändig berechnet oder aus der entsprechenden Tabelle ermittelt werden.
pi ergibt sich allgemein als:
pi = P(X ≥ Xi) - P(X > Xi + ci).
Im Falle einer Normalverteilung resultiert pi aus der Z-Transformation:
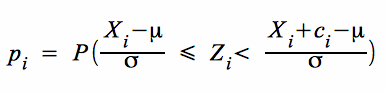
D.h. mit pi ist die Wahrscheinlichkeit gegeben, dass eine normalverteilte Zufallsvariable in einer, durch die klassierte empirische Verteilung vorgegebenen Klasse mit der Untergrenze Xi und der Breite ci realisiert wird.
Die Werte der Parameter μ und σ der Normalverteilung werden aus der empirischen Verteilung übernommen
c) Der Test auf Anpassung
Die zu testende Hypothesen lautet wieder: H0: 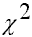 = 0, = 0,
d.h. die empirische Verteilung ist eine Stichprobe aus einer Grundgesamtheit mit einer mathematisch zu beschreibenden Dichteverteilung.
Diese kann, bezogen auf die Abb. IV-20 und IV-21, gleich- bzw. normalverteilt sein.
Getestet wird somit die Hypothese, dass die Abweichungen zwischen beiden Verteilungen zufällig sind.
Diese Hypothese ist bei einem vorgegebenen Signifikanzniveau α0 anzunehmen, wenn der empirische χ²-Wert in den Annahmebereich fällt.
Der entsprechende Grenz-Wert χ²α0 kann für die gegebene Anzahl der Freiheitsgrade φ aus der χ²-Tabelle abgelesen werden.
Wenn χ² > χ²α0 sind die Abweichungen signifikant, d.h. die empirische Verteilung folgt nicht einer theoretischen Vorlage.
Auch der Anpassungstest ist somit ein rechtsseitiger Tests. Allerdings wird jetzt eine Annahme der Hypothese angestrebt.
Die Freiheitsgrade berechnen sich jetzt über über die Anzahl der Klassen der empirischen Häufigkeitsverteilung: 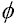 = k - 1. = k - 1.
|






