 |
Konzepte und Definitionen im Modul V-6 Konfidenzintervalle in der Regressions- und Korrelationsanalyse
Vorbemerkungen
Wir behandeln in diesem Modul in Teil A die Konfidenzschätzungen in der einfachen linearen Regressions- und Korrelationsanalyse, wie in Teil B die Konfidenzschätzungen in der multiplen Analyse.
Dabei werden in Teil A sowohl rechnerische wie grafische Schätzmodelle vorgestellt. Erstere führen zu Konfidenzintervallen für die Parameter der lineare Regressionsfunktion, letztere zu einem Konfidenzgürtel für die Regressionsfunktion der Grundgesamtheit.
Zur Vereinfachung des Schätzmodelle unterstellen wir hinreichend große Stichproben, so dass wir normalverteilte Stichprobenverteilungen annehmen können (vgl. dazu Kap. IV, Modul 6).
Teil A: Konfidenzschätzungen im einfachen linearen Regressions- und Korrelationsmodell
1. Konfidenzintervalle für die Regressionsfunktion
a) Der Konfidenzbereich für Ã
Die Schätzung der Regressionskonstanten A kann verstanden werden als Ermittlung der beiden extremsten Hypothesen, die bei einem vorgegebenen Signifikanzniveau noch mit dem Stichprobenwert von a kompatibel sind: Ã = [ A1 , A2 ]:
Abb. V-5: Das Konfidenzintervall Ã
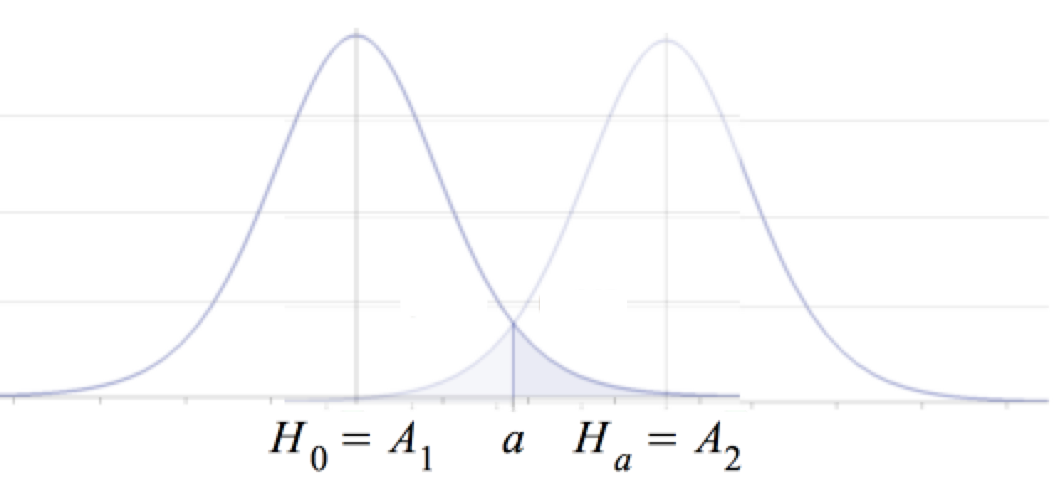
Die Konfidenz K, dass A zwischen A1 , A2 liegt, beträgt 1 - α.
Daraus ergibt sich die Formel für das Konfidenzintervall à wie folgt:
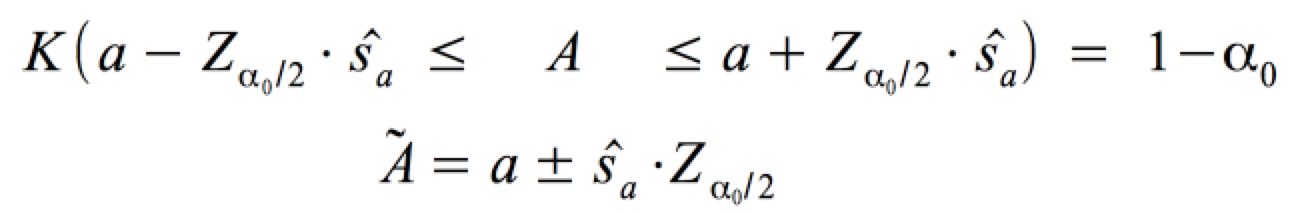
mit ŝa :
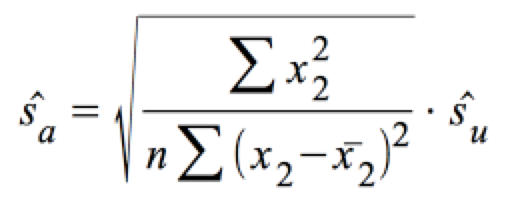
b) Der Konfidenzbereich für 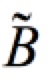
Die Schätzung des Regressionskoeffizienten kann wieder verstanden werden als Ermittlung der beiden extremsten Hypothesen, die bei einem vorgegebenen Signifikanzniveau noch mit dem Stichprobenwert von b kompatibel sind: 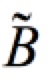 = [ B1 , B2 ]: = [ B1 , B2 ]:
Abb. V-6: Das Konfidenzintervall 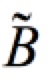
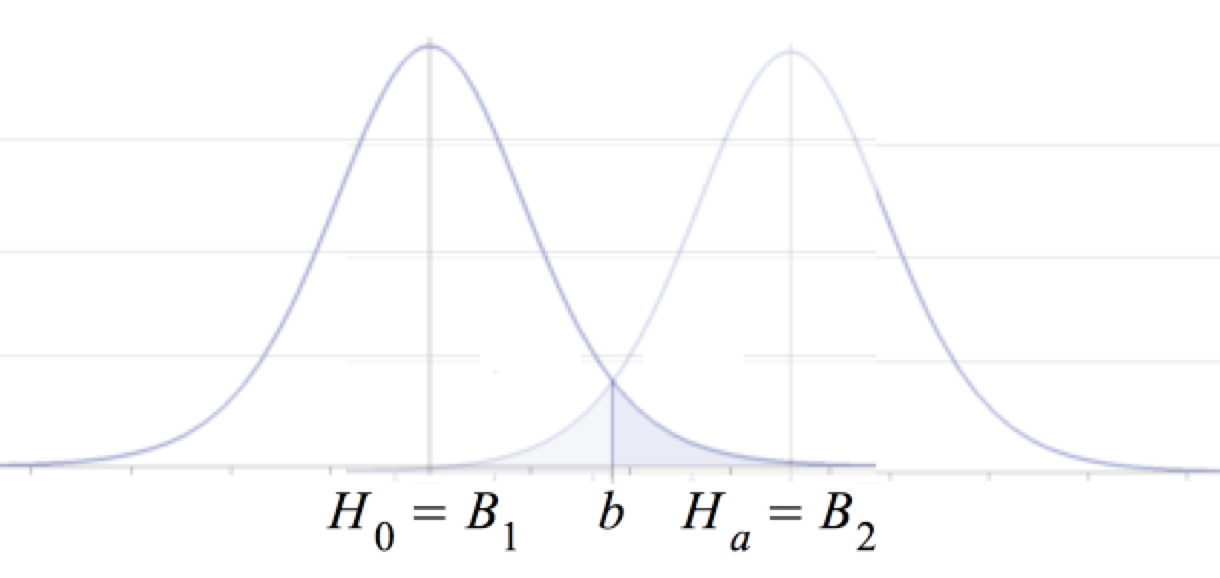
Die Konfidenz K, dass B zwischen B1 , B2 liegt, beträgt 1 - α.
Daraus ergibt sich die Formel für das Konfidenzintervall 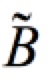 wie folgt: wie folgt:
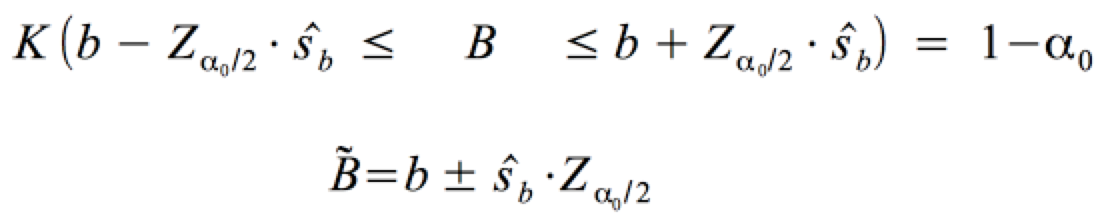
mit ŝb :
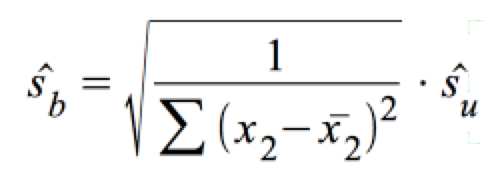
c) Der Konfidenzbereich für die Regressionsfunktion der Grundgesamtheit 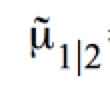
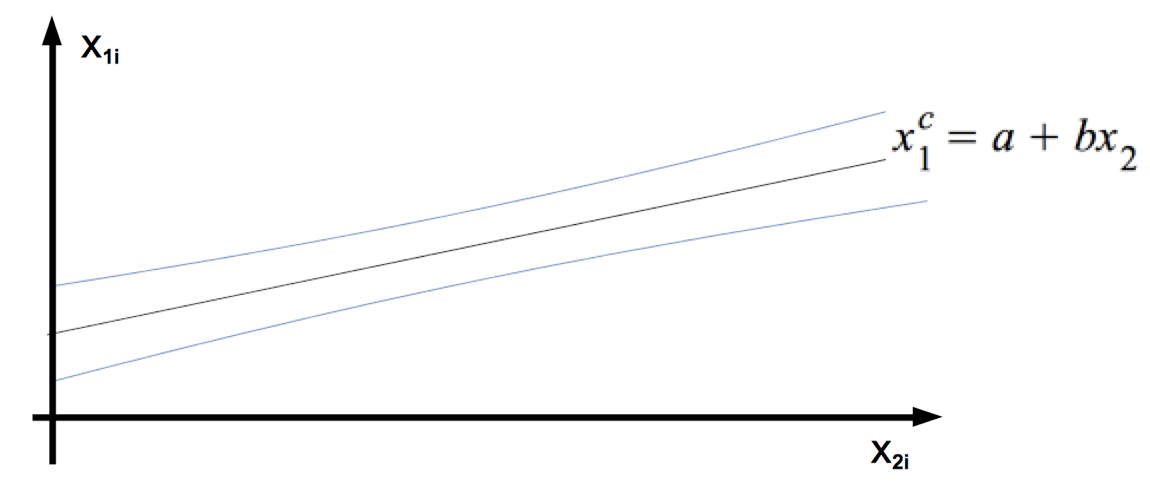
Im Folgenden wird eine simultane Schätzung beider Regressionsparameter vorgestellt. Dies führ zu einem sog. Konfidenzgürtel für die Regressionsfunktion der Grundgesamtheit:
Abb. V-6: Der Konfidenzgürtel für Xc1 = A + B X2
Die Konfidenz K, dass μ1|2 zwischen der oberen und der unteren Grenze liegt, beträgt 1 - α.
Die Formel für den Konfidenzgürtel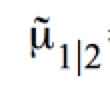 lautet: lautet:

2. Der Konfidenzbereich für die Werte der abhängigen Variable X1
Aus der Regressionsfunktion der Stichprobe lässt sich auch eine Schätzung für die bedingte Verteilung der X1 = X1|2 ableiten. Dies führ zu einem sog. Konfidenzgürtel für die Beobachtungen der X1 in der Grundgesamtheit:
Abb. V-7: Der Konfidenzgürtel für X1|2
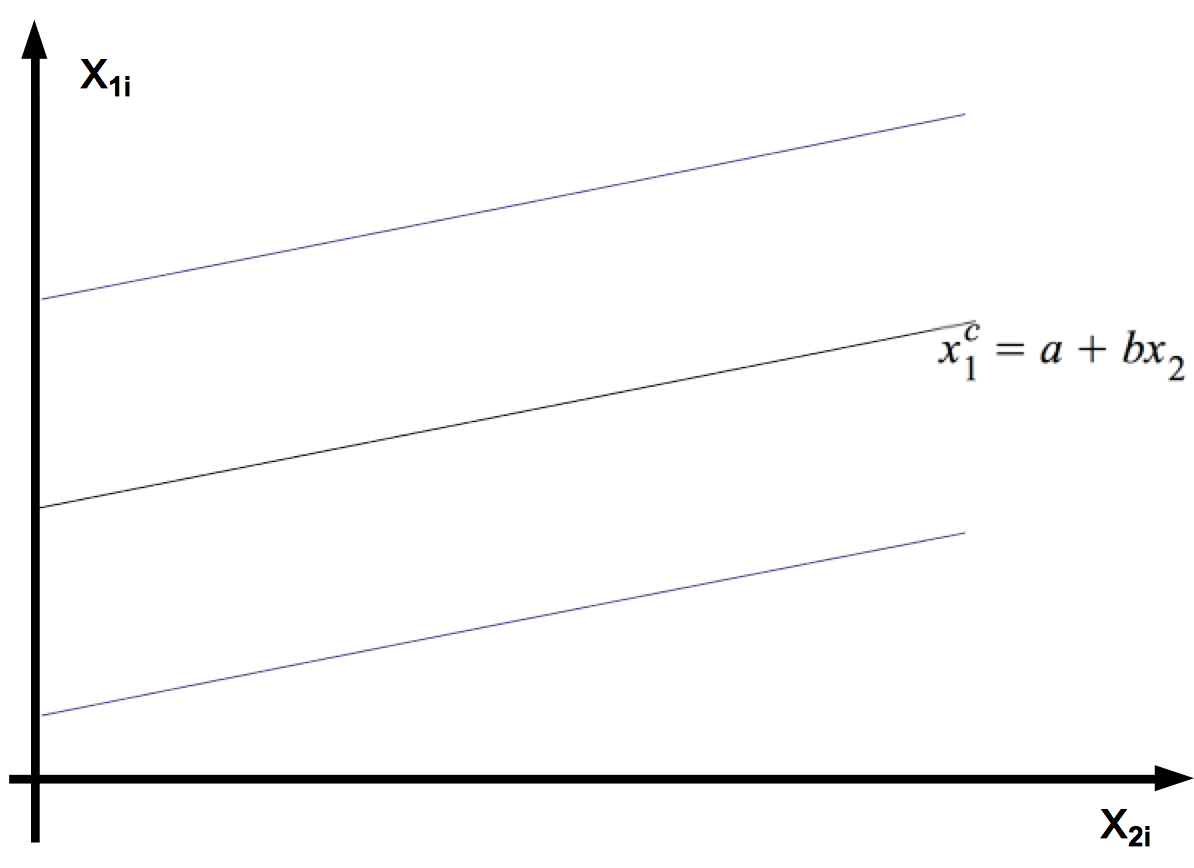
Die Konfidenz K, dass X1|2 zwischen der oberen und der unteren Grenze liegt, beträgt 1 - α.
Die Formel für den Konfidenzgürtel lautet:
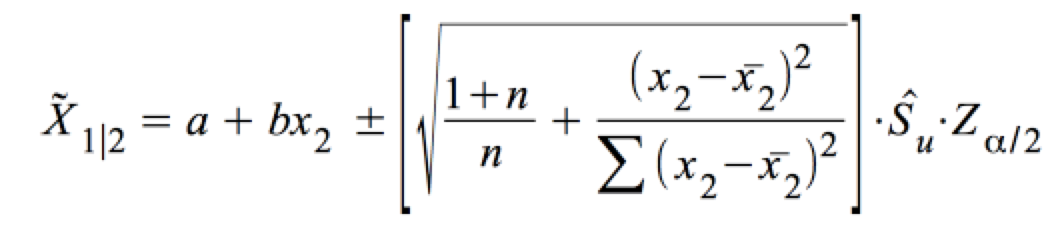
3. Der Konfidenzbereich für den Korrelationskoeffizienten der Grundgesamtheit
Konfidenzschätzungen für den Korrelationskoeffizienten sind eher unüblich. Fisher's Z-Transformation (vgl. Kap. IV, Modul 6) erfordert ein aufwendiges Verfahren der Berechnung des Konfidenzintervalls, das in der Regel auch bei Regressions- und Korrelationsanalysen
mit Programmen nicht durchgeführt wird (so z.B. nicht von SPSS).
Wenn eine Schätzung erwünscht ist, muss der Konfidenzbereich per hand berechnet werden. Dazu erfolgt hier die Angabe einer etwas vereinfachten Berechnungsformel nur in aller Kürze <(zur Ableitung vgl. Litz, Multivariate statistische Methoden, München 2000, S. 71f, bzw. Hartung/Elpelt, 1995 S. 154f).
Das Konfidenzintervall für Fisher's Zρ ist:
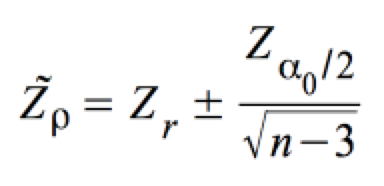 , ,
mit:
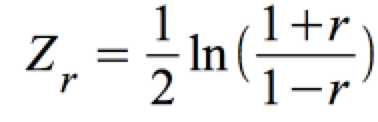
Daraus folgt:
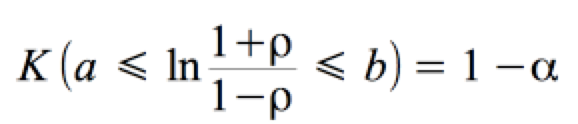 , ,
mit:
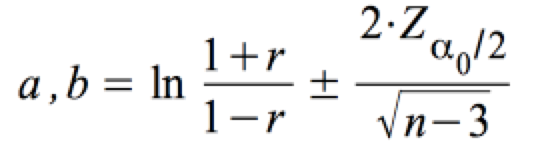
Daraus resultiert das Konfidenzintervall für ρ:
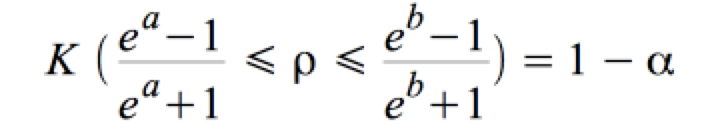 . .
Teil B: Konfidenzschätzungen im multiplen Regressions-und Korrelationsmodell
Aufgrund der Dimensionalität der multiplen Modelle lassen sich nur rechnerische Ansätze für die Konfidenzintervalle der Parameter der multiplen Regressionsfunktion formulieren.
1. Die Logik des Schätzmodells
Die Schätzung eines beliebigen multiplen Regressionsparameters " Oj " kann, wie in Teil A (Abb. V-6), verstanden werden als Ermittlung eines Bereichs zwischen den beiden extremsten Hypothesen, die bei einem vorgegebenen Signifikanzniveau noch mit dem Stichprobenwert von "o" kompatibel sind:
Õ*j = [ Oj1 , Oj2 ]
Die Konfidenz K, dass O*j zwischen Oj1 , Oj2 liegt, ergibt sich bei einem Konfidenzniveau von 1 - α wie folgt:
K( Oj1 ≤ Õ*j ≤ Oj2 ) = 1- α.
2. Das Konfidenzintervall für die Regressionsparameter
|



