| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Konzepte und Definitionen im Modul V-4 Konfidenzintervalle für die Standardabweichung σ und die Varianz σ²
Vorbemerkung
Das unbekannte σ der Grundgesamtheit wird durch die Standardabweichung ŝ der Stichprobe geschätzt. In Abhängigkeit vom Stichprobenumfang werden die Grenzen des Intervalls bei n ≤ 30 auf Grundlage einer χ²-Verteilung und bei n > 30 auf Grundlage einer Standardnormalverteilung ermittelt.
1. Die Konfidenzschätzungen für die Standardabweichung und die Varianz der Grundgesamtheit bei n ≤ 30
a) Die Ableitung der Formel für ˜σ bei n ≤ 30
Die Ableitung der Formel für das Konfidenzintervall der Standardabweichung basiert bei n ≤ 30 auf der
modifizierten Standardabweichung der Stichprobe
.
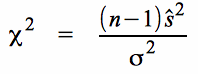
und darauf, dass diese bei einem gegebenen σ und φ = n - 1 Freiheitsgraden mit der Wahrscheinlichkeit 1 - α in einen Bereich mit der unteren Grenze χ² 1 - α/2 und der oberen Grenze χ²α/2 fällt:
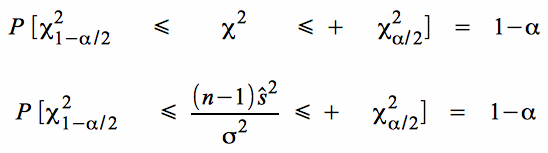 .
.
Durch Auflösung der Ungleichung nach σ erhält man die Wahrscheinlichkeit, dass ein zufällig realisiertes Stichprobenintervall den Parameter σ der Grundgesamtheit abdeckt:
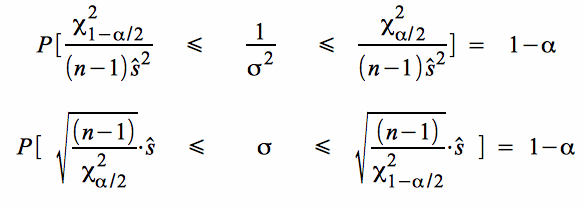 .
.
Nach dem Ziehen der Stichprobe erhält man analog zur Wahrscheinlichkeit für das Intervall die Konfidenz K, dafür dass die Standardabweichung der Grundgesamtheit σ mit einem Konfidenzniveau 1 - α im Intervall vermutet werden kann:
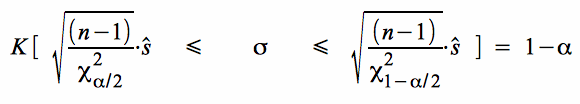 .
.
Für die Abschätzung der Varianz gilt entsprechend:
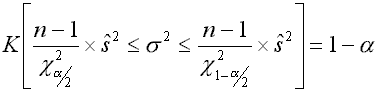
b) Die Konfidenzintervalle für σ und σ² bei n ≤ 30
Daraus resultieren der untere und der obere Grenzwert des Intervalls für die Standardabweichung der Grundgesamtheit :
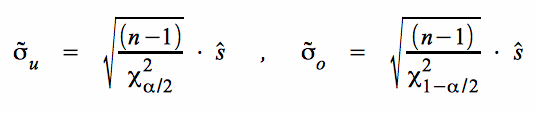 .
.
Für den unteren und der oberen Grenzwert des Intervalls für die Varianz der Grundgesamtheit:
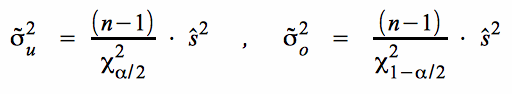 .
.
2. Die Konfidenzschätzungen für die Standardabweichung und die Varianz der Grundgesamtheit bei n > 30
a) Die Ableitung der Formel für ˜σ bei n > 30
Die Ableitung der Formel für das Konfidenzintervall der Standardabweichung basiert bei n > 30 darauf, dass die modifizierte Standardabweichung der Stichprobe
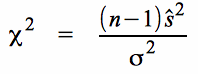 über
über 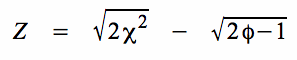
durch die Standard-Normalverteilung approximiert werden kann (vgl. Punkt C im Modul die modifizierte Standardabweichung der Stichprobe
).
Die Freiheitsgrade φ sind mit: φ = n - 1 gegeben.
Z fällt mit der Wahrscheinlichkeit 1 - α in einen Bereich mit der unteren Grenze - Zα/2 und der oberen Grenze +Zα/2:
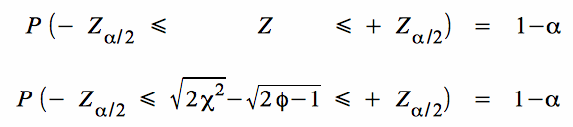 .
.
Durch Einsetzen der modifizierte Standardabweichung (s. o.) und durch Auflösung der Ungleichung nach σ erhält man die Wahrscheinlichkeit, dass ein zufällig realisierte Stichprobenintervall den Parameter der Grundgesamtheit abdeckt:
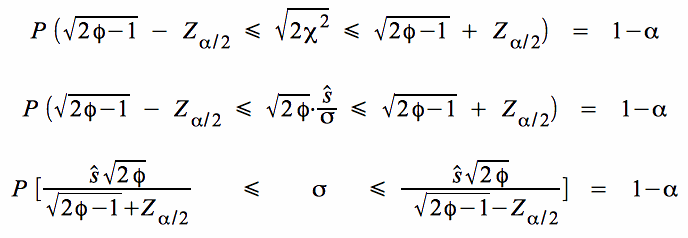 .
.
Nach dem Ziehen der Stichprobe erhält man analog zur Wahrscheinlichkeit für das Intervall die Konfidenz K, dafür dass die Standardabweichung der Grundgesamtheit σ mit einem Konfidenzniveau 1 - α im Intervall vermutet werden kann.
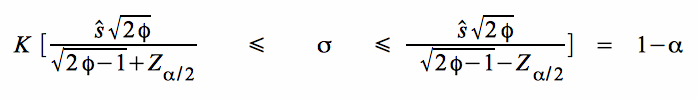
b) Das Konfidenzintervall für σ und σ² bei n > 30
Daraus resultieren der untere und der obere Grenzwert des Intervalls für die Standardabweichung der Grundgesamtheit:
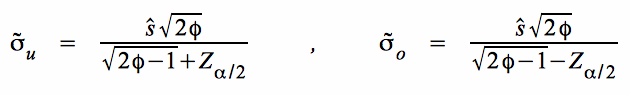 .
.
-
Das Konfidenzintervall für die Varianz ergibt sich unmittelbar aus der Quadrierung der entsprechenden Grenzen für σ.
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel05/modul04/ebene01/05__04__01__01.php3
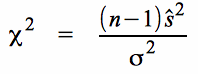
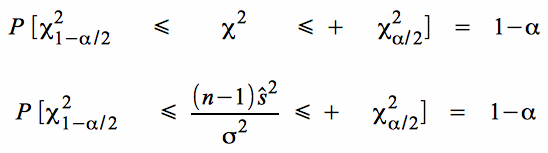 .
.
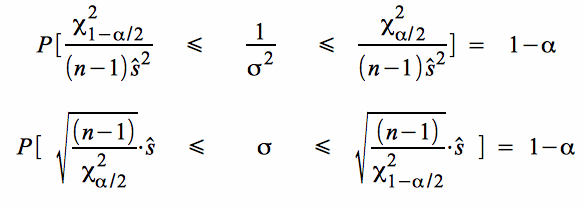 .
.
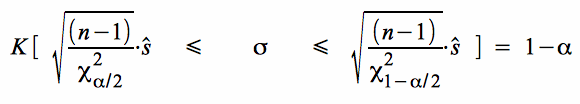 .
.
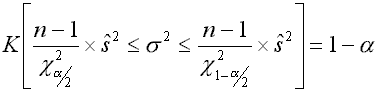
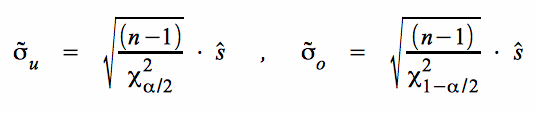 .
.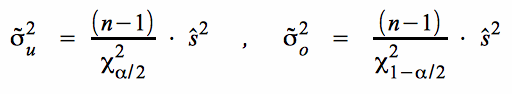 .
.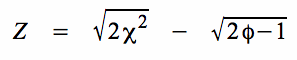
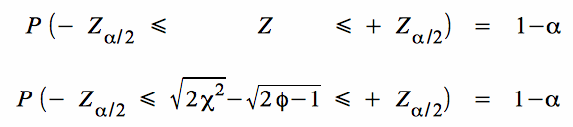 .
.
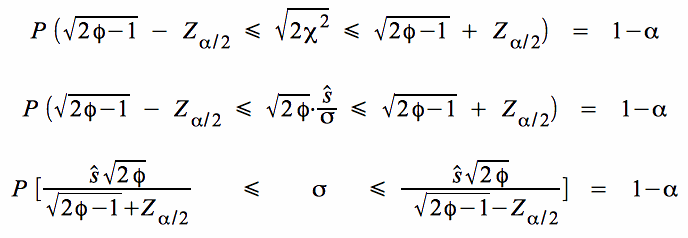 .
.
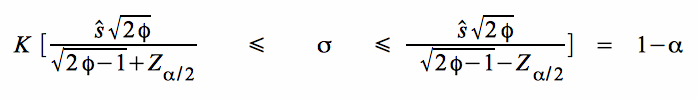
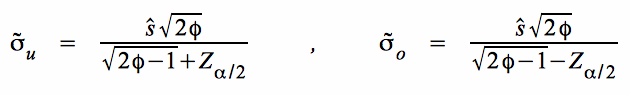 .
.