 |
Konzepte und Definitionen im Modul V-3 Konfidenzintervalle für den Anteilswert π
1. Konfidenz des Anteilswerts der Grundgesamtheit unter der Bedingung n · p · (1-p ) < 9
Die originäre Stichprobenverteilung der p ist die Binomialverteilung. Wenn n · p · (1-p ) < 9, kann die Binomialverteilung nicht durch die Normalverteilung approximiert werden. In diesem Fall werden keine Schätzungen von π durchgeführt.
2. Konfidenz des Anteilswerts der Grundgesamtheit unter der Bedingung n · p · (1-p )≥ 9
a) Vorbemerkung
Wenn n · p · (1-p ) ≥ 9, ist p annähernd normal verteilt (vgl. die Punkte C und D in
Modul "Stichprobenverteilung der p),
so dass Konfidenzintervalle bestimmt werden können.
Wenn n < 1000 muss dabei die Stetigkeitskorrektur SK = 1⁄2n vorgenommen werden.
-
Ebenso ist bei gegebenen Umständen der Endlichkeitsfaktor zu berücksichtigen.
b) Die Ableitung der Formel für ˜π
Die Ableitung der Formel für das Konfidenzintervall des Anteilswert basiert bei n · p · (1-p ) ≥ 9 auf der Wahrscheinlichkeit, dass bei einem gegebenen π die normalverteilten Anteilswerte p mit der Wahrscheinlichkeit 1 - α in einen symmetrischen Bereich um π mit der unteren Grenze p u und der oberen Grenze p o fallen.
Entsprechendes gilt für die Standardnormalvariable (im Folgenden ohne Berücksichtigung desr Stetigkeitskorrektur)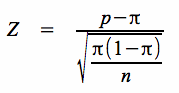 : :
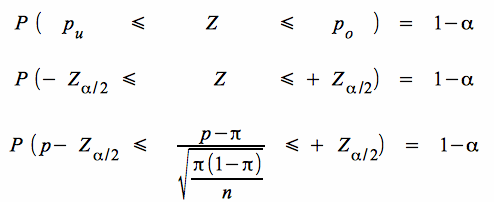 . .
Über die Standardnormalvariable erhält man durch Auflösung der Ungleichung nach π die Wahrscheinlichkeit, dass ein zufällig realisiertes Stichprobenintervall den Parameter der Grundgesamtheit abdeckt. Da π sowohl im Zähler wie im Nenner des Bruchs auftritt, muss zur Ableitung nach π, π im Nenner über p punktgeschätzt werden.
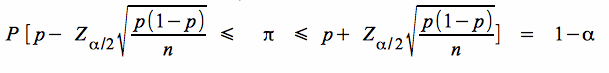 . .
Nach dem Ziehen der Stichprobe erhält man analog zur Wahrscheinlichkeit für das Intervall die Konfidenz K, dafür dass der Anteilswert der Grundgesamtheit π mit einem Konfidenzniveau 1 - α im Intervall vermutet werden kann:
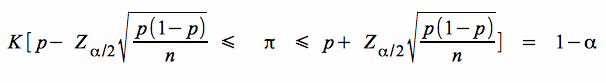 . .
c) Das Konfidenzintervall für den Anteilswert π
Bei n/N > 0,05 muss in der Formel für das Konfidenzintervall der Endlichkeitsfaktor 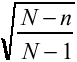 berücksichtigt werden. berücksichtigt werden.
Die Formel für das Konfidenzintervall für den Anteilswert lautet ohne Stetigkeitskorrektur:
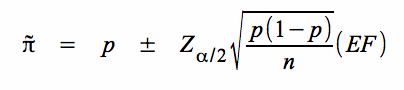
Die Formel für das Konfidenzintervall für den Anteilswert lautet mit Stetigkeitskorrektur:
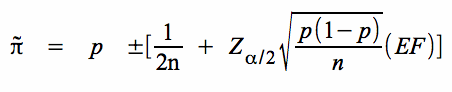
|



