 |
Beispiele und Aufgaben im Modul III-3 Stichprobenverteilungen der Anteilswerte
1. Beispiele zur Verteilung von K und p
a) Beispiel zur Verteilung von K bei n · π (1 - π) < 9
In einer sehr großen Grundgesamtheit, mit  ,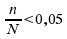
ist bekannt, dass 20% aller Personen mehr als einmal jährlich
in Urlaub fahren.
Wir prüfen zunächst die obige Bedingung
n · π (1 - π) < 9 ⇒ 15 · 0,2 · 0,8 = 2,4
Wie wahrscheinlich ist es nun, aus dieser
Grundgesamtheit eine Stichprobe der Größe n = 15 zu ziehen,
in der weniger als 5 Personen
mehrmals jährlich in Urlaub fahren.
Lösung:
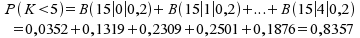
Mit diesem
Programm der Rice University
lassen sich für beliebige Binomialverteilungen Graphiken
erzeugen und die dazu gehörigen statistischen
Kennziffern der Verteilungen sowie die Wahrscheinlichkeiten berechnen, dass K bestimmte Werte annimmt.
b) Beispiel zur Verteilung von K bei n · π (1 - π) ≥ 9
Dazu können wir auf das Beispiel zur Approximation der Binomialverteilung durch eine Normalverteilung aus dem vorigen Kapitel zurückgreifen:
Im Jahre 2015 präferierten etwa 70% der jüngeren Urlauber einen Urlaub in noch fremden Ländern.
Wie groß ist die Wahrscheinlichkeit in einer Stichprobe von n = 100 zwischen 60 und 80 dieser Altersgruppe mit diesem Urlaubswunsch zu finden?
Gefragt ist damit nach der Wahrscheinlichkeit einer diskreten Variablen K:
P (60 ≤ K ≤ 80)= ?
Wir prüfen zuerst, ob die diskrete Binomial-Verteilung der Variablen hinreichend durch eine Normalverteilung approximiert werden kann.
Die Approximationsbedingung lautet:
n · π(1-π) ≥ 9, konkret: 100 · 0.7(1-0.7)= 21, d.h. ≥ 9.
Damit ist die Bedingung erfüllt.
Nun definieren wir die gesuchte Wahrscheinlichkeit für eine Normalverteilung. Unter Berücksichtigung der Stetigkeitskorrektur für K (= ± 1/2) ergibt sich diese Wahrscheinlichkeit als:
P(60 - 0.5 ≤ X ≤ 80 + 0.5).
Wir bestimmen danach die Parameter der Normalverteilung:
X hat wie K einen Erwartungswert von 70:
E(X) = n · π = 100 · 0.7 = 70
und eine Varianz von 21:
VAR(X) = n · π(1-π) = 100 · 0.7(1- 0.7) = 21.
-
Die Bestimmung der Wahrscheinlichkeit erfolgt über die Z-Transormation für K:
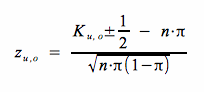> Als Wahrscheinlichkeit für die standard-normalverteilte Variable Z ergibt sich demnach:
-
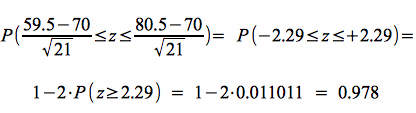
Damit beträgt die Wahrscheinlichkeit, dass in einer Stichprobe von 100 Befragten zwischen 60 und 80 Peronen mit diesem Urlaubswunsch angetroffen werden, fast 98%.
Ein externes
Applet der Rice University
veranschaulicht die Approximationsgüte graphisch und rechnerisch
für unterschiedliche Bedingungen. Mit diesem Tool können Sie die obigen Beispiele visualisieren und mit einem genaueren Rechner überprüfen.
c) Beispiel zur Verteilung von p bei n · π (1 - π) ≥ 9
Wir knüpfen dazu am obigen Beispiel an, wonach 70% der Jüngeren im Urlaub neue Länder kennenlernen möchten. Wie groß ist jetzt die Wahrscheinlichkeit, dass in einer Stichprobe von n = 100 der Anteilswert der Befragten dieser Urlaubergruppe zwischen 60 und 80% liegt?
-
Gefragt ist damit nach der Wahrscheinlichkeit: P (0.60 ≤ p ≤ 0.80)= ?
-
Die Approximationsbedingung ist bereits geprüft.
Nun definieren wir die gesuchte Wahrscheinlichkeit für eine Normalverteilung.
Unter Berücksichtigung der Stetigkeitskorrektur für p (= ± 1/2n) ergibt sich diese Wahrscheinlichkeit als:
P(0.60 - 0.005 ≤ p ≤ 0.80 + 0.005).
-
Wir bestimmen danach die Parameter der Normalverteilung:
p hat einen Erwartungswert von 0.70:
E(p) = π = 0.7
und eine Varianz von 0.0021:
VAR(p) = π(1-π)/n = 0.7(1- 0.7)/100 = 0.0021.
Die Bestimmung der Wahrscheinlichkeit erfolgt unter Berücksichtigung der Stetigketskorrektur über die Z-Transormation für p:
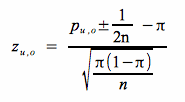
Als Wahrscheinlichkeit für die standard-normalverteilte Variable Z ergibt sich demnach:
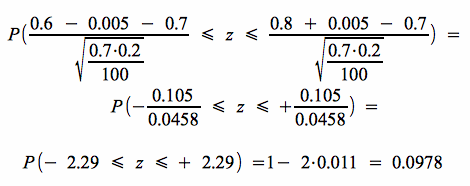
Damit beträgt die Wahrscheinlichkeit wie unter 1. b) fast 98%, dass in einer Stichprobe von 100 Haushalten 60 bis 80 % dieser Altersgruppe mit diesem Urlaunswunsch zu finden sind.
2. Aufgaben zur Verteilung von K und p
a) Aufgaben zur Verteilung von K bei n · π (1 - π) < 9
Dazu wird auf die Aufgaben im Abschnitt "Beispiele und Aufgaben" des Moduls "Binomialverteilung" sowie auf die nachstehende Aufgabe (30a) verwiesen.
Aufgabe (30 a)
Eine sehr große Grundgesamtheit
besteht zu 10% aus Gelbwählern und zu 90% aus
"Nicht"-Gelbwählern.
Berechnen Sie mit Hilfe der
Binomialverteilung die
Wahrscheinlichkeit dass, bei einer Stichprobe vom Umfang 15
drei oder mehr Gelbwähler zu finden sind.
 Diese Aufgabe können Sie in 2 Schritten
mit diesem interaktiven Tool bearbeiten.
Fertigen Sie zur Aufgabe eine Skizze an.
b) Aufgaben zur Verteilung von K bei n · π (1 - π) ≥ 9
Hierzu greifen wir auf die entsprechenden Aufgaben zur Approximation einer Binomialverteilung durch eine Normalverteilung aus dem vorigen Kapitel (Aufgaben 21a und b) und auf Aufgabe 30b) zurück:
Eine Partei hat bei der nächsten Wahl 5% aller Stimmen zu erwarten.
-
Wie gross ist die Wahrscheinlichkeit, dass bei einer Befragung von 1000 Personen genau 50 angeben, diese Partei zu wählen?
Diese Aufgabe können Sie in 4 Schritten mit diesem interaktiven Tool bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
Wie gross ist die Wahrscheinlichkeit, dass bei einer Befragung von 1000 Personen 50 Personen oder weniger angeben diese Partei zu wählen?
Diese Aufgabe können Sie in 3 Schritten mit diesem interaktiven Tool bearbeiten.
Aufgabe (30b)
Eine sehr große Grundgesamtheit
besteht zu 10% aus Gelbwählern und zu 90% aus
"Nicht"-Gelbwählern.
Berechnen Sie mit Hilfe der Normalverteilung die
Wahrscheinlichkeit, bei einer Stichprobe vom Umfang 150 einundzwanzig und mehr Gelbwähler (K ≥21) zu finden.
Diese Aufgabe können Sie in 3 Schritten mit diesem interaktiven Tool bearbeiten.
c) Aufgaben zur Verteilung von p bei n · π (1 - π) ≥ 9
Hierzu greifen wir auf die Aufgaben zu den Wahlchancen einer Partei aus dem vorherigen Abschnitt 2. b) zurück und stellen wieder Aufgaben (30c) und (31) mit interaktiven Tools. Zu den Aufgaben finden Sie am
Ende dieser Seite einen Link auf umfangreiche
Musterlösungen mit Graphiken.
Eine Partei erwartet bei der nächsten Wahl 5% aller Stimmen.
In welchem
Bereich pu - po müssten 99% aller Anteilswerte liegen, wenn diese Erwartungen nicht enttäuscht werden sollen?
Diese Aufgabe können Sie in 4 Schritten mit diesem interaktiven Tool bearbeiten.
Aufgabe (30c)
Eine sehr große Grundgesamtheit
besteht zu 10% aus Gelbwählern und zu 90% aus
"Nicht"-Gelbwählern.
Berechnen Sie mit Hilfe der Normalverteilung die
Wahrscheinlichkeit, bei einer Stichprobe vom Umfang 150:
14% und mehr Gelbwähler (p ≥ 0.14) zu finden.
Diese Aufgabe können Sie in 3 Schritten mit diesem interaktiven Tool bearbeiten.
Aufgabe (31)
Von 1000 Wellen, die täglich mit einem
Drehautomaten gefertigt werden, genügen 100 nicht den
Qualitätsanforderungen.
Aus der Tagesproduktion werden 100
Wellen zufällig ausgewählt. Mit welcher Wahrscheinlichkeit
sind davon zwischen 85 % und 95 % der Wellen von ausreichender
Qualität?
Diese Aufgabe können Sie in 6 Schritten mit diesem interaktiven Tool bearbeiten.
Für welche Zahl c ist der Ausschussanteil
in einer Stichprobe (n=100) mit einer Wahrscheinlichkeit von 0,9
kleiner/gleich c? Skizzieren Sie das Problem vor der rechnerischen
Lösung!
Diese Aufgabe können Sie in 4 Schritten mit diesem interaktiven Tool bearbeiten.
Das bekannte externes
Applet der Rice University
veranschaulicht die Approximationsgüte graphisch und rechnerisch
für unterschiedliche Bedingungen. Mit dem Tool können Sie die beiden Aufgaben visualisieren und die Ergebnisse mit einem genaueren Rechner überprüfen.
Zur
Musterlösung der Aufgaben 30 und 31
|
