 |
Konzepte und Definitionen im Modul III-3 Stichprobenverteilungen der Anteilswerte
1. Die Verteilung der Stichprobenvariablen K
Die Stichprobenanteilswerte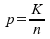 resultieren
aus dem Ziehen einer Stichprobe aus einer dichotomen
Grundgesamtheit. Ihre Verteilung kann deshalb unmittelbar aus der
Binomialverteilung von resultieren
aus dem Ziehen einer Stichprobe aus einer dichotomen
Grundgesamtheit. Ihre Verteilung kann deshalb unmittelbar aus der
Binomialverteilung von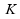 abgeleitet
werden. abgeleitet
werden.
Bei der Vorstellung der Binomialverteilung im Kapitel "Theoretische Verteilungen" hatten wir die Wahrscheinlichkeiten des Auftretens der Ereignisse A und Ā in der Grundgesamtheit mit p und q = 1-p bezeichnet. In der Gegenüberstellung von Grundgesamtheit und Stichprobe werden nun die Wahrscheinlichkeiten der Grundgesamtheit mit griechischen Buchstaben also mit π und 1-π, die der Stichprobe mit p und 1-p bezeichnet.
a) Die Verteilung der Stichprobenvariablen K bei n· π (1 - π) < 9
Die Konstruktionsprinzipien für den Erwartungswert und die Varianz dieser Binomialverteilung sind
bereits aus dem Modul “Theoretische Verteilungen“ bekannt. Für die Stichprobenverteilung der K ergeben sie sich
als: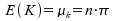 und und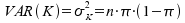 . .
-
Die Verteilung der Stichprobenvariablen K lässt sich direkt
anhand der tabellierten Wahrscheinlichkeitsfunktion der
Binomialverteilung ermitteln.
Abbildung III-9: Verteilung der Stichprobenvariablen K bei p = 0,7 und n = 20
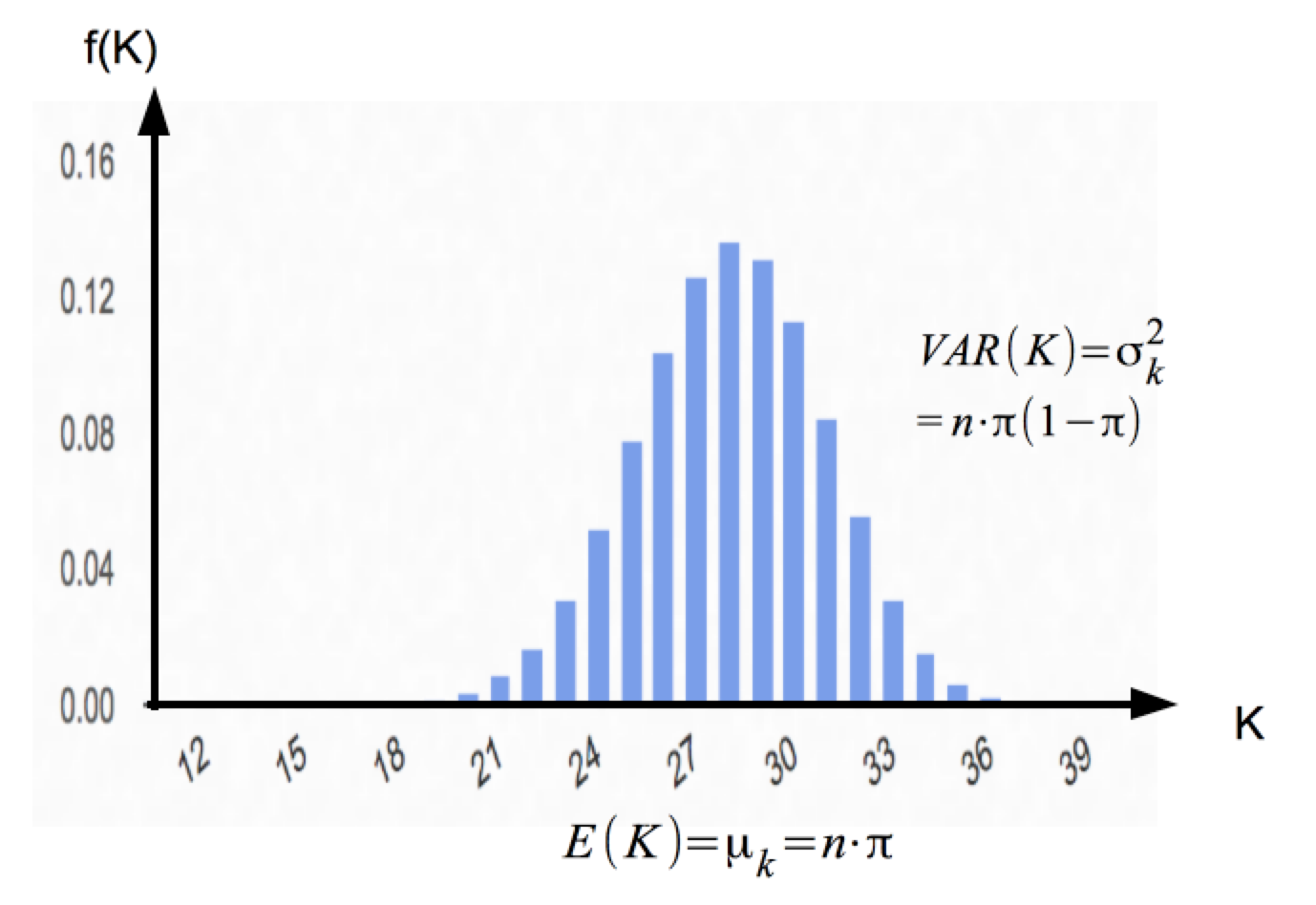
b) Die Verteilung der Stichprobenvariablen K bei n· π (1 - π) ≥ 9
Ab einer Varianz
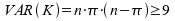 kann
die Binomialverteilung durch die Normalverteilung approximiert
werden. Hierbei ist, wie erwähnt, die diskrete Verteilung durch
eine stetige zu approximieren. Dazu ist
eine Stetigkeitskorrektur ( kann
die Binomialverteilung durch die Normalverteilung approximiert
werden. Hierbei ist, wie erwähnt, die diskrete Verteilung durch
eine stetige zu approximieren. Dazu ist
eine Stetigkeitskorrektur (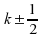 )
zu berücksichtigen. )
zu berücksichtigen.
-
Es gilt dann: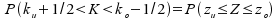 .
Auf diese Weise lassen sich die Wahrscheinlichkeiten dafür
berechnen, dass mehr als .
Auf diese Weise lassen sich die Wahrscheinlichkeiten dafür
berechnen, dass mehr als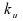 und
weniger als und
weniger als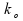 von
n Stichprobenelementen das betrachtete
Merkmal aufweisen. Hierbei
ist zu beachten, dass in von
n Stichprobenelementen das betrachtete
Merkmal aufweisen. Hierbei
ist zu beachten, dass in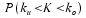 die
Werte die
Werte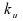 und und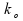 nicht
einbezogen sind. nicht
einbezogen sind.
Sollte dies doch gefordert sein, gilt hier und im Folgenden für die unter Grenze k - 1/2 und für die obere Grenze k + 1/2.
-
Die Standardnormalvariablen ergeben sich
als tabellierte Prüfgröße unter Berücksichtigung
der Stetigkeitskorrektur wie folgt:
für die untere Grenze:
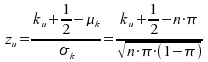 und
und
für die obere
Grenze:
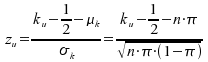
2. Die Verteilung der Stichprobenvariablen p = K/n bei n· π (1 - π) ≥ 9
a) Die Verteilung der p
Wenn K ab einer
Varianz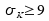 normalverteilt
ist und der Anteilswert p dann mit normalverteilt
ist und der Anteilswert p dann mit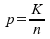 eine
Lineartransformation einer
normalverteilten Zufallsvariablen darstellt, ist nach der
Reproduktionseigenschaft der Normalverteilung auch p
normalverteilt mit den Parametern: eine
Lineartransformation einer
normalverteilten Zufallsvariablen darstellt, ist nach der
Reproduktionseigenschaft der Normalverteilung auch p
normalverteilt mit den Parametern:
-
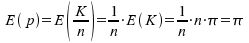
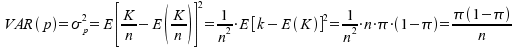
-
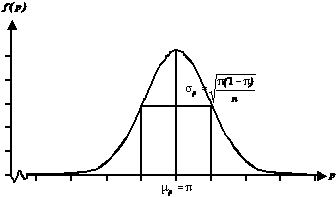
Diese Verteilung der Stichprobenanteilswerte ergibt folgendes
Bild:
Abbildung III-10: Verteilung der Stichprobenanteilswerte
b) Die Z-Transformation der Anteilswerte p
Aus den obigen Formeln läßt sich für p die Z-Transformationen ableiten.
|



