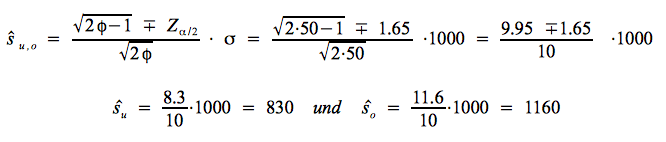| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Beispiele und Aufgaben im Modul III-2 Stichprobenverteilungen der modifizierten Standardabweichungen
1. Beispiele
a) Beispiel einer Stichprobenverteilung bei n≤ 30
Als
Beispiel gehen wir von einer normalverteilten Grundgesamtheit mit dem
Parameter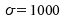 (also
(also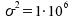 )
aus. Es
werden daraus Stichproben vom Umfang n = 20 gezogen, d.h.:
)
aus. Es
werden daraus Stichproben vom Umfang n = 20 gezogen, d.h.: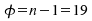 .
.
In welchem Bereich
werden nun 90% aller Stichprobenstandardabweichungen
liegen?
Die
Wahrscheinlichkeit ist vorgegeben, es gilt also, die Intervallgrenzen
für
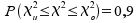 zu
bestimmen.
zu
bestimmen.
Die entsprechenden
Werte können für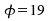 der
tabellierten Funktion der
der
tabellierten Funktion der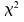 -Verteilung
entnommen werden. Die 10% Wahrscheinlichkeit außerhalb des
gesuchten Intervalls ist aufzuteilen in jeweils 5% am unteren und 5%
am oberen Ende der Verteilung, so dass in der Tabelle die
-Verteilung
entnommen werden. Die 10% Wahrscheinlichkeit außerhalb des
gesuchten Intervalls ist aufzuteilen in jeweils 5% am unteren und 5%
am oberen Ende der Verteilung, so dass in der Tabelle die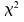 -Werte
für eine Wahrscheinlichkeit von 0,05 und 0,950 nachzuschlagen
sind. So gilt:
-Werte
für eine Wahrscheinlichkeit von 0,05 und 0,950 nachzuschlagen
sind. So gilt:
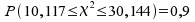
 Mit folgendem Applet der Universität von Iowa lassen sich die Grenzen bei φ = 19 und einer Wahrscheinlichkeit von 0.9 für den Bereich bestimmen und graphisch darstellen. Dazu geben Sie in der ersten Eingabzeile die Freiheitsgrade und in der zweiten die Werte für α mit 0.95 und 0.05 in das Fenster rechts neben dem Gleichheitszeichen ein.
Mit folgendem Applet der Universität von Iowa lassen sich die Grenzen bei φ = 19 und einer Wahrscheinlichkeit von 0.9 für den Bereich bestimmen und graphisch darstellen. Dazu geben Sie in der ersten Eingabzeile die Freiheitsgrade und in der zweiten die Werte für α mit 0.95 und 0.05 in das Fenster rechts neben dem Gleichheitszeichen ein.
Die Grenzen des
gesuchten Intervalls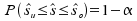 sind dann wie folgt bestimmt:
sind dann wie folgt bestimmt:
Untere Grenze:
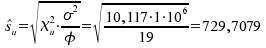
Obere
Grenze:
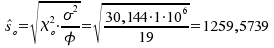 und wir erhalten:
und wir erhalten:
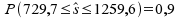
Damit ergibt sich zwischen den Grenzwerten eine Spanne von 530.
b) Beispiel einer Stichprobenverteilung bei n > 30
Unter Bezug auf das obige Beispiel bestimmen wir nun bei einer Wahrscheinlichkeit von 0.9 den mittleren Bereich für Stichproben im Umfang von n = 51.
Bei φ = n - 1 = 50 ergeben sich die Grenzwerte wie folgt:
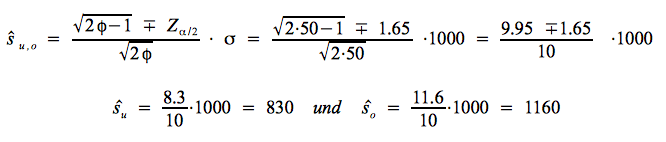
Damit ergibt sich zwischen den Grenzwerten eine Spanne von 530. Im Vergleich zu einer Stichprobe im Umfang von n = 20 erbringt also ein etwa 2.5-faches n eine Reduktion der Spanne zwischen den Grenzen um 60%.
c) Simulationen von Stichprobenverteilungen der s, s² und ŝ²
 Mit diesem
Programm der Rice University lassen sich im Fenster "Begin"
Stichprobenverteilungen aus unterschiedlichen, auch selbst definierten
Grundgesamtheiten (1. Fenster), in selbstgewählten Schritten
oder Anzahl von Stichproben (2. Fenster) für die Stichprobenverteilungen
s, s² und ŝ² (3. und 4. Fenster) erzeugen und graphisch darstellen sowie die dazugehörigen
statistischen Kennziffern der Verteilungen berechnen.
Mit diesem
Programm der Rice University lassen sich im Fenster "Begin"
Stichprobenverteilungen aus unterschiedlichen, auch selbst definierten
Grundgesamtheiten (1. Fenster), in selbstgewählten Schritten
oder Anzahl von Stichproben (2. Fenster) für die Stichprobenverteilungen
s, s² und ŝ² (3. und 4. Fenster) erzeugen und graphisch darstellen sowie die dazugehörigen
statistischen Kennziffern der Verteilungen berechnen.
Ein Vergleich der Verteilungen der nicht erwartungstreuen Varianz s² mit der erwartungstreuen Varianz ŝ² zeigt deutlich, dass erstere kaum geeignet ist, auf die Varianz der Grundgesamtheit zu schliessen.
2. Aufgaben
Im Folgenden haben Sie die
Möglichkeit, Aufgabenstellungen zur Stichprobenverteilung
der Varianzen anhand von vorgegebenen Aufgaben und interaktiven Tools zu bearbeiten oder anhand bereitgestellter
Musterlösungen nachzuvollziehen. Dazu finden Sie am Ende dieser Seite
einen Link auf die Musterlösungen zu
diesen Aufgaben.
Aufgabe (29)
Der Durchmesser von Wellen, die auf einer
bestimmten Drehbank gefertigt werden, ist normalverteilt mit einer
Varianz von 0,01 mm2.
a) Wie groß ist die
Wahrscheinlichkeit, dass die Varianz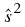 von
20 zufällig ausgewählten Wellen zwischen 0,005325 mm2
und 0,01587 mm2 liegt?
von
20 zufällig ausgewählten Wellen zwischen 0,005325 mm2
und 0,01587 mm2 liegt?
 Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 6 Schritten findet sich unter diesem Link.
Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 6 Schritten findet sich unter diesem Link.
Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
b) In
welchem Bereich liegen bei n = 25 die Standardabweichungen der Stichproben mit einer Wahrscheinlichkeit von 0.90?
 Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 4 Schritten findet sich unter diesem Link.
Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 4 Schritten findet sich unter diesem Link.
c) In
welchem Bereich liegen die Standardabweichungen von Stichproben im Umfang von n = 50 bei einer Wahrscheinlichkeit von 0.90?
 Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 3 Schritten findet sich unter diesem Link.
Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 3 Schritten findet sich unter diesem Link.
Zur
Musterlösung der Aufgabe 29
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel02x5_Stichprobenverteilungen/modul02_Stichprobenverteilungen~~lder~~lmodifizierten~~lStandardabweichungen/eb
ene02_Beispiele~~lund~~lAufgaben/02x5__02__02__01.php3
![]() (also
(also![]() )
aus. Es
werden daraus Stichproben vom Umfang n = 20 gezogen, d.h.:
)
aus. Es
werden daraus Stichproben vom Umfang n = 20 gezogen, d.h.:![]() .
.![]() zu
bestimmen.
zu
bestimmen.![]() der
tabellierten Funktion der
der
tabellierten Funktion der![]() -Verteilung
entnommen werden. Die 10% Wahrscheinlichkeit außerhalb des
gesuchten Intervalls ist aufzuteilen in jeweils 5% am unteren und 5%
am oberen Ende der Verteilung, so dass in der Tabelle die
-Verteilung
entnommen werden. Die 10% Wahrscheinlichkeit außerhalb des
gesuchten Intervalls ist aufzuteilen in jeweils 5% am unteren und 5%
am oberen Ende der Verteilung, so dass in der Tabelle die![]() -Werte
für eine Wahrscheinlichkeit von 0,05 und 0,950 nachzuschlagen
sind. So gilt:
-Werte
für eine Wahrscheinlichkeit von 0,05 und 0,950 nachzuschlagen
sind. So gilt:![]()
 Mit folgendem Applet der Universität von Iowa lassen sich die Grenzen bei φ = 19 und einer Wahrscheinlichkeit von 0.9 für den Bereich bestimmen und graphisch darstellen. Dazu geben Sie in der ersten Eingabzeile die Freiheitsgrade und in der zweiten die Werte für α mit 0.95 und 0.05 in das Fenster rechts neben dem Gleichheitszeichen ein.
Mit folgendem Applet der Universität von Iowa lassen sich die Grenzen bei φ = 19 und einer Wahrscheinlichkeit von 0.9 für den Bereich bestimmen und graphisch darstellen. Dazu geben Sie in der ersten Eingabzeile die Freiheitsgrade und in der zweiten die Werte für α mit 0.95 und 0.05 in das Fenster rechts neben dem Gleichheitszeichen ein.![]() sind dann wie folgt bestimmt:
sind dann wie folgt bestimmt: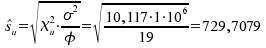
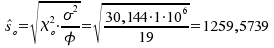 und wir erhalten:
und wir erhalten:![]()