| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Beispiele und Aufgaben im Modul III-1 Stichprobenverteilungen des arithmetischen Mittels
1. Beispiele
a) Ableitung einer Stichprobenverteilung der X̄ aus einer kleinen Grundgesamtheit
Zunächst soll das Ziehen von Stichproben und die Generierung einer Stichprobenverteilung des arithmetischen Mittels anhand einer kleinen Grundgesamtheit demonstriert werden:
Eine Gesamtheit vom Umfang N = 5 lasse sich wie nachstehend charakterisieren:
-
|
i
|
x1
|
f1
|
|
1
|
2
|
1
|
|
2
|
4
|
1
|
|
3
|
6
|
1
|
|
4
|
8
|
1
|
|
5
|
10
|
1
|
Diese Verteilung weist einen Mittelwert μ = 6 und eine Varianz σ² = 8 auf.
Jetzt werden aus dieser
Gesamtheit Auswahlen ohne Wiederholung vom Umfang n = 2 gezogen.
Wir bestimmen die exakte
Verteilung der Stichprobenmittel und
stellen diese graphisch dar! Dabei lassen sich 10 unterschiedliche Stichproben ziehen.
Abbildung III-6: Verteilung der
Stichprobenmittelwerte bei n = 2
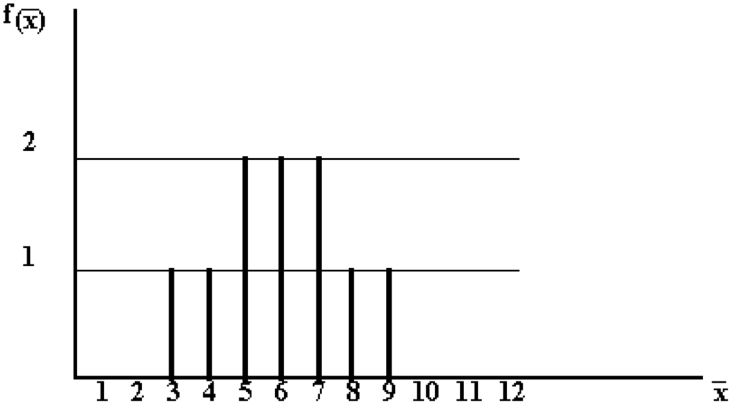
Erwartungswert und Varianz dieser Verteilung ergeben sich aus der Verteilung (vgl. Abb. III-6) wie folgt:
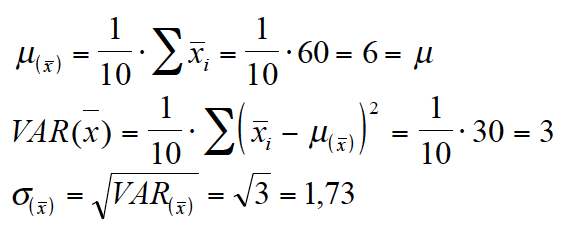
Der Mittelwert der Stichprobenmittel beträgt 6. Die Varianz der Stichprobenmittel ist 3.
Unter Berücksichtigung des Endlichkeitsfaktors kann die Varianz auch aus den Parametern der Grundgesamtheit abgeleitet werden:
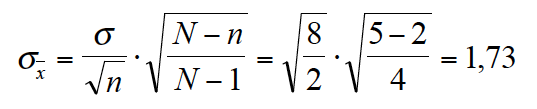
Wie groß ist nun die Wahrscheinlichkeit dafür, dass
das Stichprobenmittel Werte zwischen 4 und
6 einschließlich dieser Grenzen annimmt?
Durch Auszählen ergibt sich eine Wahrscheinlichkeit von 0.6, d.h. 60% aller denkbarer Stichproben ergeben Mittelwerte zwischen 4 und 6.
Eine detaillierte Darstellung der insgesamt gezogenen Stichproben und eine exakte Ableitung ihrer Parameter findet sich unter dem Link für die Musterlösungen zur Aufgabe (26) am Ende des Kapitels.
b) Beispiel einer Stichprobenverteilung der X̄ bei bekanntem σ
Im Folgenden betrachten wir
die Verteilung der Stichprobenmittelwerte, die sich bei einer Ziehung
von Stichproben im Umfang von n = 36 aus einer beliebig verteilten
Grundgesamtheit von Nettomonatslöhnen eines bestimmten
Berufszweiges mit einem arithmetischen Mittel von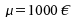 und
einer Standardabweichung von
und
einer Standardabweichung von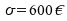 ergeben.
Es gilt dann:
ergeben.
Es gilt dann:
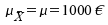 und
und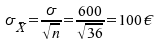
Diese Verteilung ist in
Abb. III-7 dargestellt:
Abbildung III-7: Verteilung der
Stichprobenmittelwerte
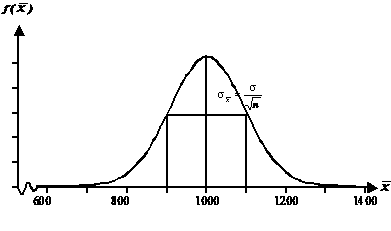
Mit welcher Wahrscheinlichkeit fallen die Stichproben in den ± 2σ-Bereich um E(X̄) = 1000?
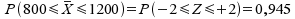 .
.
Nach den für
Normalverteilungen geltenden Gegebenheiten erbringen somit etwa 95%
aller Stichproben durchschnittliche Stundenlöhne zwischen 800
und 1200 €.
In welchen symmetrischen Bereich falle nun 99% aller Stichprobenmittelwerte?
Gesucht sind damit X̄u und X̄o in: P(X̄u ≤ X̄ ≤ X̄o) = 0.99.
Über: P(zu ≤ z ≤ zo) = 0.99 mit: zu = - 2.58 und zo = + 2.58 erhalten wir mittels der Z-Transformation:
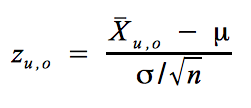 .
.
X̄u,o = μ ± z · σ/√n = 1000 ± 2.58 · 600/√36 = 1000 ± 258.
Damit liegt X̄ mit einer Wahrscheinlichkeit von 0.99 im Bereich: 742 ≤ X̄ ≤ 1258.
c) Beispiel einer Stichprobenverteilung der X̄ bei unbekanntem σ (n = 25)
Wir variieren nun bei einem μ von 1000 die obige Aufgabe, indem wir annehmen, dass σ unbekannt ist und durch ŝ = 500 aus einer Stichprobe von n = 25 ersetzt werden kann.
In welchem symmetrischen Bereich sind nun 99% aller X̄ zu erwarten?
Die relevante Prüfgrösse ist t-verteilt. Gesucht sind damit tu und to im Ausdruck P(tu ≤ t ≤ to) = 0.99.
Mit:
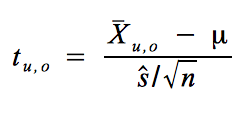 .
.
erhalten wir bei φ = n - 1 = 24:
X̄u,o = μ ± t · ŝ/√n = 1000 ± 2.797 · 500/√25.
Damit liegt X̄ mit einer Wahrscheinlichkeit von 0.99 im Bereich: 720.3 ≤ X̄ ≤ 1279.7.
2. Aufgaben
Im Folgenden haben Sie die
Möglichkeit, weitere Aufgabenstellungen zur Stichprobenverteilung
der Mittelwerte anhand von vorgegebenen Aufgaben und interaktiven Lösungstool zu bearbeiten und bereitgestellte
Musterlösungen nachzuvollziehen. Dazu finden Sie am Ende dieser Seite
einen Link auf die Musterlösungen zu
diesen Aufgaben.
Aufgabe (27)
Nehmen Sie Stellung zu folgenden Aussagen:
Der Erwartungswert der
arithmetischen Mittel einer Zufallsvariablen in gleichartigen
Stichproben aus derselben Grundgesamtheit ist gleich dem
arithmetischen Mittel der Grundgesamtheit.
Der Erwartungswert der
Standardabweichungen einer Zufallsvariablen in gleichartigen
Stichproben aus derselben Grundgesamtheit ist gleich der
Standardabweichung dieser Zufallsvariablen in der Grundgesamtheit.
Der Betrag des Standardfehlers des
arithmetischen Mittels einer Zufallsvariablen verhält sich
umgekehrt proportional zum Betrag der Varianz dieser Variablen in
der Grundgesamtheit.
Der Betrag des Standardfehlers des
arithmetischen Mittels einer Zufallsvariablen verhält sich
proportional zum Stichprobenumfang.
Das Verhältnis
Standardabweichung zu arith. Mittel in
einer Stichprobe ist immer gleich diesem Verhältnis in der
zugehörigen Grundgesamtheit.
 Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 4 Schritten findet sich
Ein interaktives Tool zur Bearbeitung dieser Aufgabe in 4 Schritten findet sich
unter diesem Link. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
Eine ausführliche Darstellung der Lösung von Aufgabe (27) finden Sie im Link am Ende des Kapitels.
Aufgabe (28)
Ein Sägewerk liefert Grubenstempel als
geschlossene Partie von 1200 Stück, deren Länge
normalverteilt ist mit einem Mittelwert von 60 cm und einer Varianz
von 36 cm.
a) Es werden Stichproben vom Umfang
36 gezogen.
Eine ausführliche Darstellung der Lösung von Aufgabe (28a) finden Sie im Link am Ende des Kapitels.
b) Es werden Stichproben ohne
Zurücklegen vom Umfang 100 gezogen.
Eine ausführliche Darstellung der Lösung von Aufgabe (28b) finden Sie im Link am Ende des Kapitels.
c) Die Varianz der Partie ist nicht bekannt. Es werden Stichproben vom Umfang von 9 gezogen. Die Stichprobe ergibt ein ŝ von 7 cm.
Zu
den Musterlösungen der Aufgaben 26 bis 28 b
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel02x5_Stichprobenverteilungen/modul01_Stichprobenverteilungen~~ldes~~larithmetischen~~lMittels/ebene02_Beispi
ele~~lund~~lAufgaben/02x5__01__02__01.php3

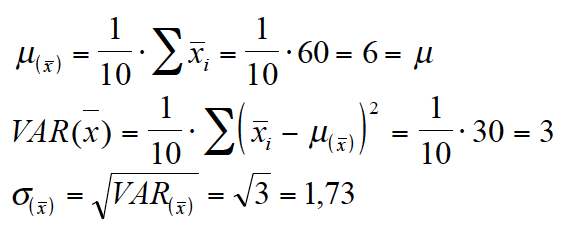
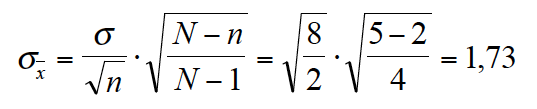
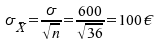

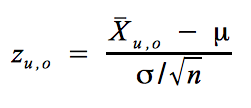 .
.
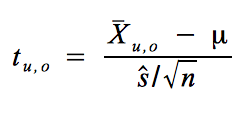 .
.