1. Beispiele zur t-Verteilung

Die Abweichungen von den fahrplanmäßigen Ankunftszeiten eines Linienbusses seien t-verteilt.

Bitte versuchen Sie die Aufgaben unter Verwendung einer Tabelle zuerst selbst zu lösen!

• Eine detaillierte Tabelle findet sich hier.

• Einen Rechner zum Berechnen der Ergebnisse und zur Erzeugung einer entsprechenden Graphik finden Sie wieder unter diesem externen Link .

• Eine grafische Darstellung der t-Verteilung liefert auch der t-Verteilung-Plotter von N. Johnston .

a) Aufgabe 1

• Wie groß ist die Wahrscheinlichkeit, dass ein konkreter Bus bei 10 Freiheitsgraden mit einer Abweichung von maximal ± 0.7 Min. an einer Haltestelle eintrifft?

• Lösung: Gesucht ist:

  P( - 0.7 ≤ t ≤ + 0.7) = 1 - 2 · P (t ≥ + 0.7) = 1 - 2 · 0.25 = 0.5 (vgl. Tab.II-6, Randwahrscheinlichkeiten der t-Verteilung)

  Die Wahrscheinlichkeit, daß der Bus innerhalb der angegebenen Zeitspanne von ± 0.7 Min. eintrifft, beträgt 50 %.

b) Aufgabe 2

• In welchem Bereich bewegen sich bei 13 Freiheitsgraden 80% der (symmetrischen) Abweichungen von der fahrplanmäßen Ankunftszeit?

• Lösung:

  Zu b): Gesucht ist t_u, t_o in:

  P(t_u ≤ t ≤ t_o) = 0.8, bzw. P (t ≥ t_o) = 0.1

  bei φ = 13 ⇒ t_o = 1.35 (vgl. Tab.II-6, Randwahrscheinlichkeiten der t-Verteilung).

  80% der Abweichungen liegen im Bereich von ± 1.35 Minuten.

c) Aufgabe 3

• In welchem Bereich bewegen sich bei 35 Freiheitsgraden 95% der (symmetrischen) Abweichungen von der fahrplanmäßen Ankunftszeit?

• Lösung:

  Zu c): Bei φ = 35 kann die t-Verteilung durch die Standardnormalverteilung approximiert werden! Gesucht ist deshalb:

  P( z_u ≤ z ≤ z_o) = 0.95 bzw. P (z ≥ z_o) = 0.025.

  ⇒ z _u = 1.96 (vgl. Tab.II-2, Randwahrscheinlichkeiten der Standardnormalverteilung).

  Damit liegen 95% der Abweichungen im Bereich von etwa ± 2 Minuten.

2. Aufgaben zur t-Verteilung

Im Folgenden haben Sie die Möglichkeit Aufgabenstellungen zur t-Verteilung anhand eines interaktiven Tools zu bearbeiten oder anhand bereitgestellter Musterlösungen nachzuvollziehen.
Dazu finden Sie am Ende der Aufgabe ein interaktives Tool zur Bearbeitung sowie am Ende dieser Seite einen Link auf die ausführlichen Musterlösungen zu diesen Aufgaben als pdf-Datei.

Aufgabe (24)
Eine Zufallsvariable sei t-verteilt mit 20 Freiheitsgraden. Bestimmen Sie die Wahrscheinlichkeit, dass t

1. zwischen -1,325 und 1,725 liegt,

2. etwas über 2,5 liegt und

3. kleiner als -0,86 ist!

4. In welchem mittleren Bereich liegen ihre Realisationen mit einer Wahrscheinlichkeit von 99 %?

Ein interaktives Tool zur Bearbeitung der Aufgabe in 4 Schritten findet sich unter diesem externen Link. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in dieser pdf-Datei zu berücksichtigen.

Aufgabe (25)
Vergleichen Sie die Güte der Approximation einer t - Verteilung mit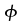= 20,30,50 und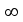 Freiheitsgraden an eine entsprechende Normalverteilung anhand der jeweiligen t₀ - bzw. z₀ - Werte. Verwenden Sie das 99. Zentil als Grundlage des Vergleichs.

Ein interaktives Tool zur Bearbeitung der Aufgabe in 4 Schritten findet sich unter diesem externen Link.

^{Zur Musterlösung der Aufgaben (24) und (25).}

---

Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 7 Benutzern im Durchschnitt mit "eher gut" bewertet.

2/2 100 % Fortschritt

 

| Vorheriger Arbeitsschritt | Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächstes Kapitel |