 |
Beispiele und Aufgaben im Modul II-1 Die Binomialverteilung
1. Beispiele
a) Berechnung der Wahrscheinlichkeiten nach der Formel
Eine Befragung hat ergeben, dass 90% der
Studierenden während ihres Studiums sporadisch oder regelmäßig jobben. Wie
wahrscheinlich ist es dann, eine Stichprobe von n = 6 Personen zu
ziehen, in der nur jeder zweite, also genau 3 Personen in ihrem Studium gejobbt haben?
Lösung: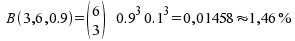 . .
Wie wahrscheinlich ist es, eine Stichprobe von n = 6
zu ziehen, in der niemand jemals gejobbt hat?
Lösung: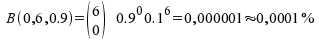
b) Ermittlung der Wahrscheinlichkeiten aus der Tabelle
Da unter Klausurbedingungen die Arbeit mit der Wahrscheinlichkeitstabelle erforderlich ist, soll das richtige Lesen der Tabelle im
Folgenden kurz geübt werden.
Für eine
Region, in der ein Urlauber seine Ferien verbringen möchte, sei
bekannt, dass nur noch jede 4te Ferienwohnung frei ist. Unser
Urlauber wählt aus einer Adressenliste drei Angebote aus, d.h.
n = 3. Er zieht sozusagen eine Stichprobe im Umfang von drei
Adressen. Wie hoch ist die Wahrscheinlichkeit, dass mindestens eine
der drei Wohnungen noch frei ist, d.h. dass k ≥ 1 ist?
Damit die erforderlichen Bedingungen erfüllt
sind, muss die Auswahl der Adressen ausreichend zufällig sein.
Die Konstanz der Wahrscheinlichkeiten kann vorausgesetzt werden,
wenn im gewünschten Gebiet mehr als 60 Wohnungen vorhanden
sind. Der Auswahlsatz ist somit kleiner als 5%. Da es nur zwei
mögliche Ereignisse gibt, liegt für K eine
Binomialverteilung vor.
Ermitteln wir zunächst aus der Tabelle der
Binomialverteilung (vgl. Tabelle II-1) die Wahrscheinlichkeit dafür,
dass alle drei Wohnungen frei waren, also B(3,3,0.25). Dazu wird
zunächst in der Vorspalte n = 3 gesucht. In diesem Tabellenblock
kann nun im Schnittpunkt der Zeile k = 3 mit der Spalte p = 0,25 die
entsprechende Wahrscheinlichkeit abgelesen werden. Diese liegt bei
0,0156. Da für unsere Aufgabenstellung aber entscheidend ist,
mit welcher Wahrscheinlichkeit mindestens eine der Wohnungen frei
ist, müssen hierzu noch die Wahrscheinlichkeiten für k = 2
und k = 1 addiert werden. Wir erhalten eine Wahrscheinlichkeit von
immerhin fast 58%:
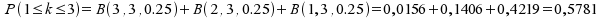 . .
Wenn, wie in diesem Fall, nach der
Wahrscheinlichkeit dafür gefragt ist, dass das Ereignis A für
mindestens ein Element der Stichprobe eintritt, also
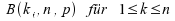 ,
so kann man die entsprechende Wahrscheinlichkeit natürlich auch
ermitteln, indem von der Wahrscheinlichkeit des sicheren Ereignisses
P(S)=1 die Wahrscheinlichkeit für B(0, n, p) subtrahiert wird. In
unserem Beispiel: ,
so kann man die entsprechende Wahrscheinlichkeit natürlich auch
ermitteln, indem von der Wahrscheinlichkeit des sicheren Ereignisses
P(S)=1 die Wahrscheinlichkeit für B(0, n, p) subtrahiert wird. In
unserem Beispiel:
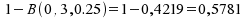
c) Berechnung der Wahrscheinlichkeiten über die Symmetrieeigenschaft
Die Lösung zum Beispiel 1) kann auf Grund
der Symmetrieeigenschaft
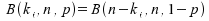 auch
aus der Tabelle bestimmt werden. Dazu wird die Verteilung
auch
aus der Tabelle bestimmt werden. Dazu wird die Verteilung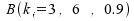 durch die Verteilung
durch die Verteilung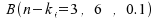 ersetzt. Der dazugehörende Wert für p findet sich für n = 6 und
k = 3 im 3. Zahlenblock. ersetzt. Der dazugehörende Wert für p findet sich für n = 6 und
k = 3 im 3. Zahlenblock.
d) Veranschaulichung der Approximation der Binomialverteilung durch die Normalverteilung
Dazu werden zwei Verteilungen einander gegenübergestellt, die sich bei gleichem p = o,1 nur bezüglich des Stichprobenumfangs n = 20 vs. n = 100 unterscheiden.
Abbildung II-2: Vergleich zweier Binomialverteilungen bei n = 20 vs. n = 100
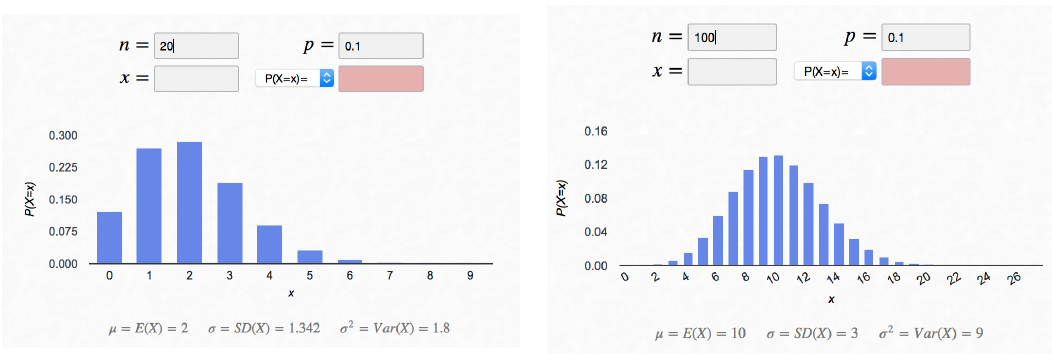
Hier ist gut zu sehen, dass die ursprünglich schiefe Verteilung der f( k i) bei n =100 und VAR(K) = 9 bereits ausreichend symmetrisch ausfällt.
e)Applets zur graphischen Ermittlung von Verteilung
 Zur graphischen Darstellung von Binomial-Verteilungen wird auf folgendes externe Angebot der Universität von Iowa
verwiesen, das auch der ABB. II-2 zugrunde lag. Hier können Sie sich die Graphiken für beliebige n und p erzeugen und sich die Funktionsparameter berechnen lassen.
Zur graphischen Darstellung von Binomial-Verteilungen wird auf folgendes externe Angebot der Universität von Iowa
verwiesen, das auch der ABB. II-2 zugrunde lag. Hier können Sie sich die Graphiken für beliebige n und p erzeugen und sich die Funktionsparameter berechnen lassen.
Weitere
statistische Kalkulationen und Graphiken stehen unter diesem
Link (Tables) und den von M. Bognar entwickelten applets zur Auswahl bereit.
Bitte lesen Sie sich vorher die Hinweise durch und wählen
eine geeignete Anwendung aus.
Anmerkungen:
Dargestellt sind u.a.
die in diesem Kapitel behandelten
kontinuierlichen
Funktionen (Normalverteilung, Student-t-Verteilung,
Chi-Quadrat-Verteilung) und die
diskrete Funktion (Binomialverteilung).
Es sind sowohl Darstellungen zu den
Es können sowohl:
Rechnungen (über
Calculator) wie
graphische
Darstellungen (über Plotter) als auch
Zufallswerte (über
Random Numbers)
auf der Basis selbst gewählter Parameter
berechnet bzw. erstellt werden.
2.Aufgaben
a) Aufgaben mit Ergebniskontrollen
Aufgabe 1
Bitte geben ermitteln Sie die folgenden Wahrscheinlichkeiten mit Hilfe der Tabelle. Beachten Sie dabei, daß nur Wahrscheinlichkeiten bis 0,5 tabelliert sind. Sie müssen daher auf die Symmetrieeigenschaft der Binomialverteilung zurückgreifen:
B(ki,n,p)=B(n-ki,n,1-p).
Aufgabe a
Aufgabe 2
Ein Wanderer, der ausgiebig die Wälder der Harzregion durchstreift hat, stellt nach seiner Heimreise fest, daß er sich bei seinen Streifzügen durch das Unterholz 3 Zecken "eingefangen" hat. Da er nicht gegen Infektionen, die von diesen Spinnentieren übertragen werden können, geimpft ist, informiert er sich besorgt über das Risiko einer Infektion. Er erfährt, daß zwar kein Risiko einer Infektion mit der gefährlichen FSME (Hirnhautentzündung) besteht, daß aber durchschnittliche jede 5. Zecke in diesem Gebiet Träger der Borreliose-Bakterien ist, die ebenfalls schwerwiegende Erkrankungen hervorrufen können.
Als erfahrener Statistiker berechnet der Wanderer sofort das Risiko, sich infiziert zu haben.
b) Aufgaben aus dem Aufgabensatz mit
Musterlösungen
Im Folgenden haben Sie
die Möglichkeit, weiteren binomialen Fragestellungen anhand von
vorgegebenen Aufgaben und bereitgestellten Musterlösungen
nachzugehen. Dazu finden Sie am Ende dieser Seite einen Link auf die
Musterlösungen zu diesen Aufgaben.
Aufgabe (15)
Die Wahrscheinlichkeit, dass
ein Papagei das Sprechen erlernt, beträgt nach Literaturangaben
0,4. Der Sprachunterricht wird in Einzelsitzungen abgehalten, die
Experimente verlaufen unabhängig voneinander.
Der Mozartliebhaber
Wolfgang A. möchte wissen, wie wahrscheinlich es ist, dass
zwei seiner gefiederten Freunde (er besitzt fünf Exemplare) ihm
später einmal etwas vortragen. Wolfgang A. denkt an das Duett
aus der Zauberflöte.
Wie wahrscheinlich
ist es, dass Wolfgang A. auf die Mitwirkung der fünf Tiere
verzichten muss?
Wie wahrscheinlich
ist es, dass wenigstens einer der Papageien so begabt ist, ein Solo
aus dem Don Giovanni darbringen zu können?
Ein Jahr später genießt Wolfgang A.
die erhoffte Solopartitur in Papageienversion. Das Duett fällt
aus, obwohl der Zoohändler gesagt hat: ,,Wenn Sie ein Duett
haben wollen, fahren Sie mit fünf am besten."
Berechnen
Sie den Wert, auf den der Händler sich bezog! Bestimmen Sie
zusätzlich die Varianz!
Aufgabe (16)
Ein Kleiderverkäufer
rechnet bei jedem Kunden mit einer Wahrscheinlichkeit von 0.2, ihm
einen Anzug verkaufen zu können.
Bestimmen Sie die
Wahrscheinlichkeit dafür, dass von fünf Kunden, die
unabhängig voneinander das Geschäft betreten, a) keiner, b)
zwei oder drei, c) wenigstens einer, d) alle einen Anzug kaufen.
Berechnen Sie zusätzlich E(X) und die Varianz bei n = 20 Kunden.
Zur
Musterlösung der Aufgaben
(15) und (16).
|



