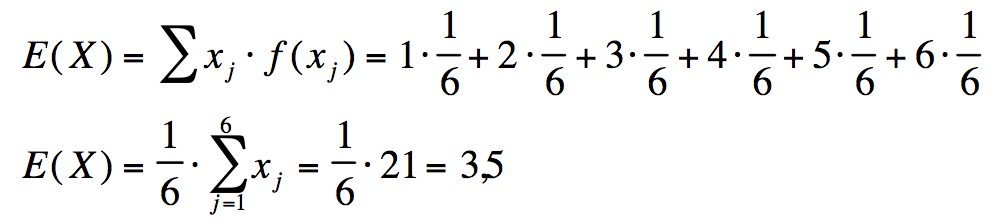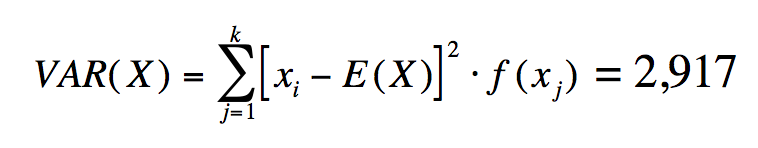Schritt 2
Vorbemerkung: Da die Schritte 2 -4 sehr aufwändig zu bearbeiten sind, kann auch auf die Lösung der Aufgabenstellung zu Aufgabe 11 im Link am Endes des Moduls zurückgegriffen werden.
Nehmen Sie nun die Zuordnung der Elementarereignisse zu den
Ausprägungen der Zufallsvariablen vor und bestimmen Sie die
Wahrscheinlichkeitsfunktion.
Benutzen Sie das Programm Webstat (im Tool-Bereich),
um diese Wahrscheinlichkeitsfunktion grafisch darzustellen
Schritt 3
Berechnen Sie nun den Erwartungswert E(X) sowie die Varianz VAR(X)
der Zufallsvariable:
Schritt 4
Berechnen und zeichnen Sie die Verteilungsfunktion F(xj)
der Zufallsvariable.
Schritt 5
Denken Sie über die folgende Frage nach:
Welche Möglichkeiten hätten Sie, die
Wahrscheinlichkeitsfunktion zu bestimmen, wenn sie nicht von der
Annahme idealer Würfel ausgehen könnten, d.h. die
tatsächliche Wahrscheinlichkeit für das Fallen bestimmter
Augenzahlen nicht bekannt wäre (tatsächlich erfüllt
kaum ein Würfel diese Voraussetzungen).
b) Weitere Aufgaben zu diskreten Verteilungen
Im Folgenden haben Sie die
Möglichkeit, verteilungstheoretischen Fragestellungen anhand von
vorgegebenen Aufgabenstellungen und bereitgestellten Musterlösungen
nachzugehen. Dazu finden Sie am Ende dieser Seite einen Link
auf die Musterlösungen zu diesen Aufgaben.
Aufgabe (11)
Erläutern Sie am Beispiel der
Augensumme beim Würfeln mit zwei Würfeln die Begriffe
Zufallsvariable, Wahrscheinlichkeitsfunktion und
Verteilungsfunktion. Stellen Sie beide Funktionen tabellarisch und
graphisch dar. Berechnen Sie den Erwartungswert und die Varianz für
die Augenzahl.
Wie hoch musste der Einsatz
mindestens sein, wenn in einem Spiel der Spielleiter die Augensumme
als Gewinn auszahlt, damit die Bank im Durchschnitt keinen Verlust
macht?
Aufgabe (12)
Eine
Zufallsvariable X besitze die folgende Wahrscheinlichkeitsfunktion:
|
x
|
8
|
12
|
16
|
20
|
24
|
|
f(x)
|
1/8
|
1/6
|
3/8
|
1/4
|
1/12
|
Bestimmen Sie und zeichnen Sie die
zugehörige Verteilungsfunktion.
Berechnen Sie den Erwartungswert E(X) und die Varianz VAR(X)
Aufgabe (13)
Eine Lebensversicherung über 60.000,-
DM kostet einen 40-jährigen Versicherungsnehmer eine
Jahresprämie von 450,- DM. Die Wahrscheinlichkeit, dass ein 40
jähriger im laufenden Jahr stirbt, beträgt nach den
Sterbetafeln der Versicherung 0,004. Wie hoch ist die Gewinnerwartung
der Versicherung für den Abschluss in
diesem Jahr?
c) Aufgaben zur stetigen Verteilungen
Aufgabe (14)
Die Dichtefunktion
einer stetigen Zufallsvariablen X sei:
f(x) = k · x für 5 ≤ x ≤ 9 mit k > 0 und f(x) = 0 für alle anderen x.
Bestimmen Sie k und zeichnen Sie die Dichtefunktion!
Wie lautet die Verteilungsfunktion von X ?
Wie groß sind Median,
Erwartungswert und Varianz?
Eine Musterlösungen
dazu finden Sie am Ende dieser Seite im Link
.
Zur Musterlösung der
Aufgaben
(11) bis (14)
letzte Änderung am 4.3.2021 um 20:14 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel01_Grundlagen~~lder~~l~~lWahrscheinlichkeitsrechnung/modul04_Zufallsvariablen~~lund~~lihre~~lVerteilung/eben
e02_Beispiele~~lund~~lAufgaben/01__04__02__01.php3