 |
Konzepte und Definitionen im Modul IX-3 Maße der prädiktiven Assoziation
1. Der konstruktive Ansatz des prädiktiven Modells
a) Die prognostische Konstruktionslogik
Das PRE- Maß von Goodman/Kruskal folgt - im Gegensatz zur kausalanalytischen Begründung der χ2 basierten Kontingenzmaße - einer prädiktiven (prognostischen) Konstruktionslogik. Dabei wird geprüft, in welchem Ausmaß eine Prognose verbessert werden kann, wenn man der Prognose zusätzlich zu den Informationen einer eindimensionalen Häufigkeitsverteilung auch noch die Informationen einer zweidimensionalen Verteilung zugrunde legt.
b) Die Definition der Prognosefehler
Im Modell werden zwei Arten von Vorhersagefehlern einander
gegenübergestellt: Zum einen der Vorhersagefehler F 1 auf der
Grundlage der eindimensionalen Häufigkeitsverteilung und
zum anderen der Vorhersagefehler F 2 auf der Basis der zweidimensionalen Häufigkeitsverteilung:
2. Das Maß der prädiktiven Assoziation λ (PRE-Maß nach Goodman/Kruskal)
a) Die Ausgangsdefinition
-
λ ist definiert als Maß der relativen Fehlerreduktion:
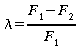
mit 0 ≤ λ ≤ 1 .
-
Bei einem vollständigen Zusammenhang zwischen den beiden Variablen lässt sich die Ausprägung von Yi|X j genau vorhersagen. Dann ist der Prognosefehler F2= 0, und somit λ = 1.
Existiert kein Zusammenhang zwischen den beiden Variablen, läßt sich die Prognose nicht verbessern. Dann gilt F2 = F1 und λ = 0.
b) Die Definition unter Berücksichtigung der Kausalität der Beziehung
3. Die Eigenschaften des PRE-Maßes
-
λ lässt sich für alle Skalenniveaus berechnen.
Aus dem Konstruktionsprinzip folgt eine lineare Beziehung zwischen der prozentualen Fehlerreduktion und dem prozentualen Anwachsen des Maßes. Mit diesem Wert lässt sich demnach die Stärke des Zusammenhangs zwischen den Variablen im Bereich 0 < λ < 1 korrekt wie folgt beziffern:
-
λ = 0,25: ein schwacher Zusammenhang,
-
λ = 0,50: ein mittlerer Zusammenhang,
-
λ = 0,75: ein starker Zusammenhang.
Generell ist jedoch anzumerken, dass das Maß der prädiktiven Fehlerreduktion sehr stark auf das Vorliegen eindeutiger Modi in den Tabellenspalten reagiert, da jede Häufigkeit ausserhalb der modalen Klasse als Fehler gezählt wird, d.h. je undeutlicher die Modi ausgeprägt sind, desto geringer fällt λ aus.
Die Stärke des Zusammenhangs ist ausserdem abhängig von der Richtung des Zusammenhangs (vgl. dazu den nächsten Arbeitsschritt "Beispiele und Aufgaben")
4. Eine Veranschaulichung der Rechenschritte
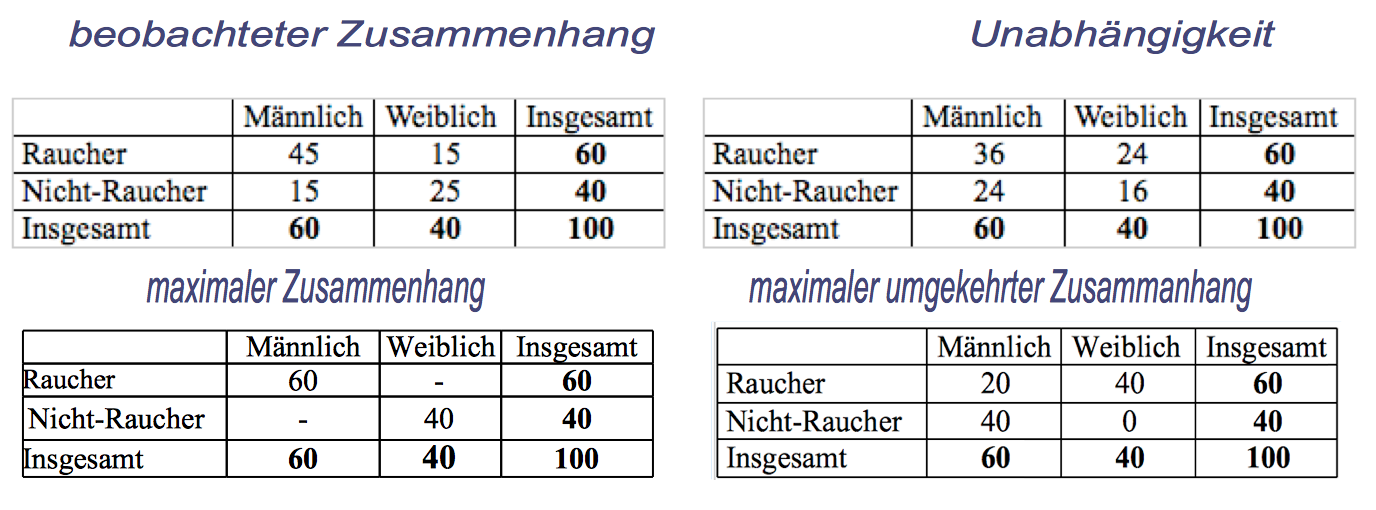
Im Folgenden soll die Berechnung der verschiedenen Konstellationen am Beispiel des Rauchverhaltens demonstriert werden:
Abbildung 9-5: Formen des Rauchverhaltens
-
Die Berechnung von λ für den beobachteten Zusammenhang (linke Tabelle oben)
F1 = N - max(fi) = 100 - 40 = 60
F1 ist fr alle nachfolgenden Berechnungen identisch.
F2 = ∑ [ f.j - max(fij ] = (60 - 45) + (40 - 25) = 30
-
Die Berechnung von λ bei Unabhängigkeit (rechte Tabelle oben)
F1 = 40
F2 = ∑ [ f.j - max(fij ] = (60 - 36) + (40 - 24) = 40
-
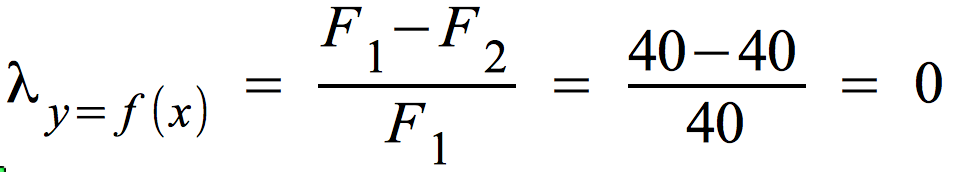
Die Berechnung von λ bei maximaler Abhängigkeit (linke Tabelle unten)
F1 = 40
F2 = ∑ [ f.j - max(fij ] = (60 - 60) + (40 - 40) = 0
-
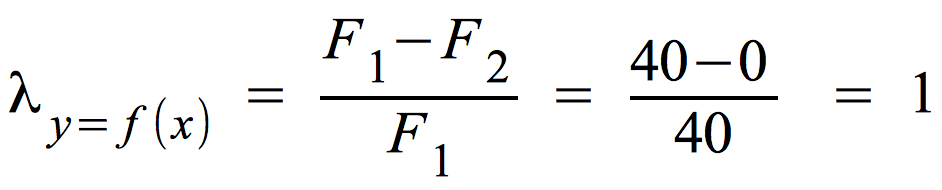
Die Berechnung von λ bei "maximaler" umgekehrter Abhängigkeit (rechte Tabelle unten)
F1 = N - max(fi) = 40
F2 = ∑ [ f.j - max(fij ] = (60 - 40) + (40 - 40) = 20
-
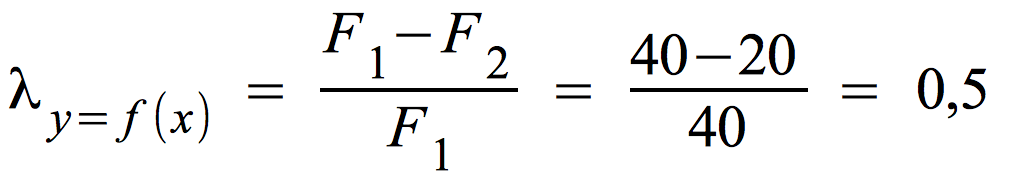
Fazit:
-
Im Falle der beobachteten Verteilungen ergibt sich mit λ = 0,25 ein schwacher Zusammenhang.
-
Bei Unabhängigkeit erhalten wir λ = 0, also keinen rechnerischen Zusammenhang.
-
Bei vollständiger Abhängigkeit erhalten wir λ = 1, also eine rechnerische Bestätigung des vollständigen Zusammenhangs.
-
Bei "maximalem" umgekehrten Zusammenhang erhalten wir λ = 0,5, also nur die rechnerische Bestätigung eines mittleren Zusammenhangs.
|
hingewiesen: 
wenn sich die Richtung der Abhängigkeit umkehrt und 
, wenn keine eindeutige Richtung gegeben ist.
