| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Konzepte und Definitionen im Modul Chi-Quadrat-basierte Kontingenzmaße
1. Die Modellanforderungen
Wie gesehen, erlaubt χ2 noch keine Aussage über die Stärke des Zusammenhanges
zwischen zwei Variablen.
Im Gegensatz zu χ2 sollte die Maßzahl möglichst unabhängig
von der Tabellenform und der Tabellengröße sowie von der Skalierung der Variablen sein. Dazu ist es notwendig, diese Faktoren auszuschalten bzw. ihren Einfluss zu vermindern.
Ausserdem soll die Maßzahl ein Maximum von "1" nicht überschreiten.
2. Die Modellansätze
In der Literatur finden sich verschiedene Ansätze, diese Ziel zu erreichen. Im Folgenden werden die gebräuchlichsten Meßmodelle vorgestellt und ihre Vor- und Nachteile diskutiert.
Man erkennt an den Formeln, wie
versucht wird, den Einfluß der Anzahl der Beobachtungen sowie
der Tabellenform auf unterschiedliche Weise auszugleichen und den Effekt der Quadrierung der Differenzen zwischen den beobachteten und den erwarteten Werten abzumildern.

3. Die Eigenschaften der Maßzahlen
phi
liegt für 2 x 2-Tabellen zwischen 0 und 1 und kann für größere Tabellen schnell Werte > "1" annehmen.
Cramer's V liegt für beliebig große
Tabellen zwischen 0 und 1 und ist bei 2 x 2- bzw. 2 x 3-Tabellen identisch mit der Formel für
phi.
min(z-1,s-1)
bedeutet, daß jeweils der kleinere Wert eingesetzt wird.
Pearson's C
liegt zwischen 0 und einem Maximalwert Cmax, der sich aus der Form der
Tabelle ergibt:
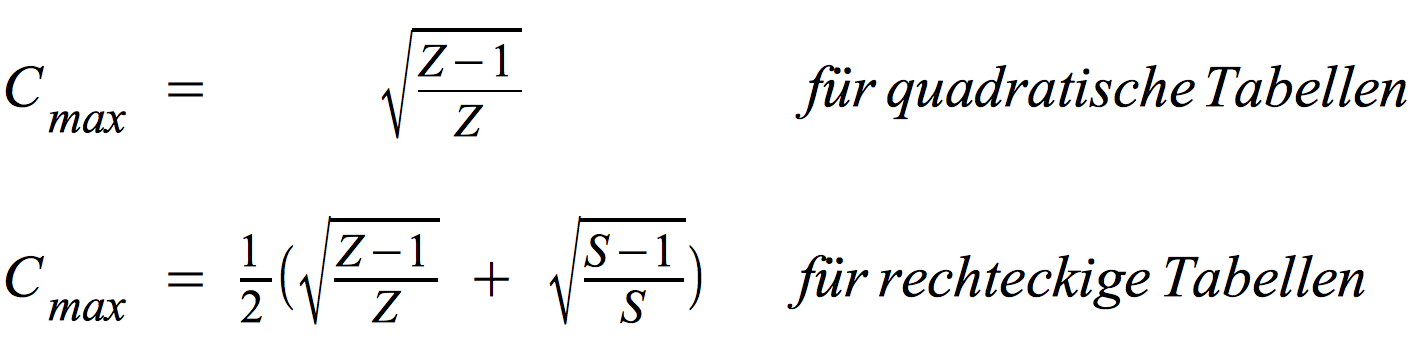
4. Die empfohlene Maßzahl Ckorr
Aus Pearson's C und Cmax erhält man den korrigierten
Kontingenzkoeffizienten Ckorr dann als:
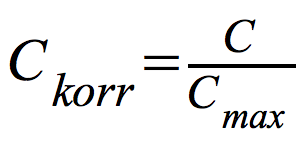
mit: 0 ≤ Ckorr ≤ 1 .
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel09_Zusammenhangsma~~sze~~lf~~uer~~lnominalskalierte~~lDaten/modul01x1_Chi-Quadrat-basierte~~lKontingenzma~~s
ze/ebene01_Konzepte~~lund~~lDefinitionen/09__01x1__01__01.php3