 |
Konzepte und Definitionen im Modul IX-1 Die Maßzahl Chi-Quadrat
1. Die Konstruktion des χ2-Maßes
a) Der Vergleich von Kontingenz- und Indifferenztabelle
Im vorangegangenen Kapitel hatten wir einer zweidimensionale Häufigkeitstabelle realer Beobachtungen, der sog. Kontingenztabelle eine (aus deren Randverteilungen abgeleitete) Tabelle der bei Unabhängigkeit der beiden Variablen zu erwartenden Häufigkeiten, der sog. Indifferenztabelle gegenüber gestellt.
Es ist nun naheliegend, eine Maßzahl für die Stärke des Zusammenhanges zwischen zwei nominal skalierten Variablen zu konstruieren, die auf den Abweichungen der empirisch in der Kontingenztabelle vorgefundenen Häufigkeiten von den bei Unabhängigkeit erwarteten Häufigkeiten in der Indifferenztabelle basiert.
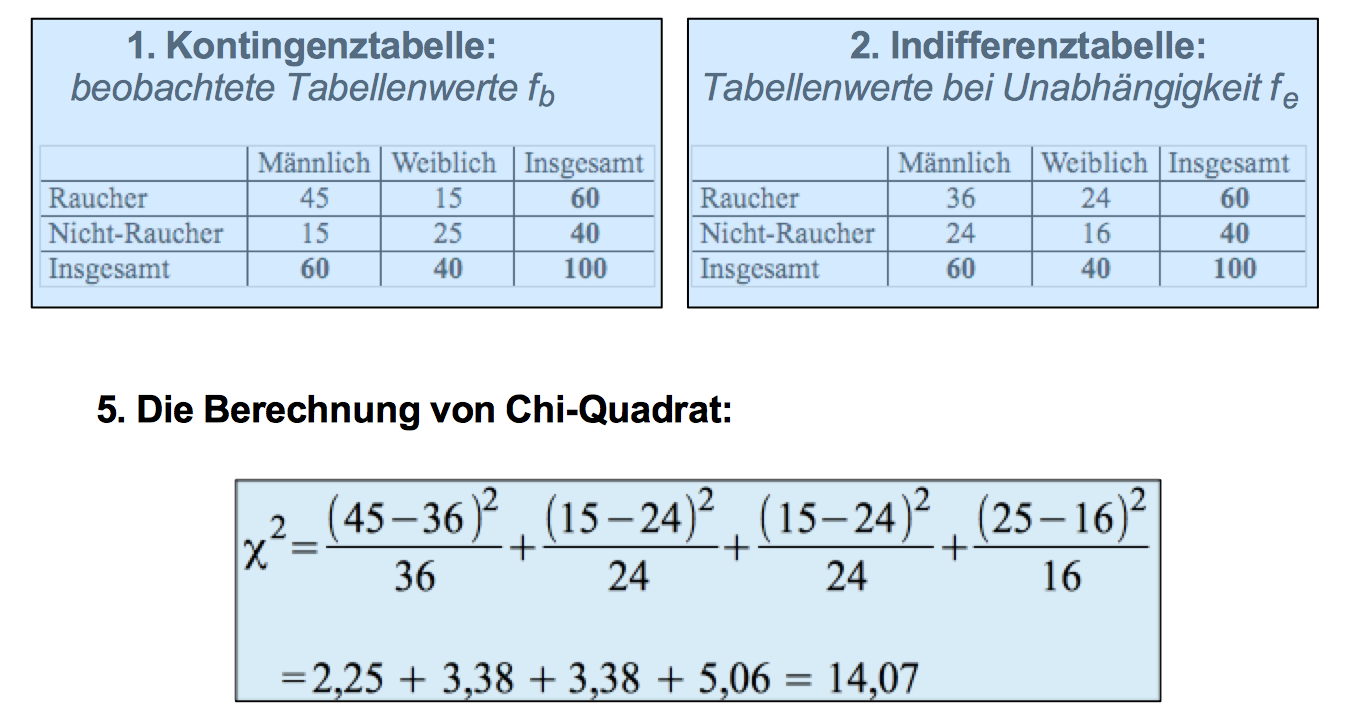
Diese Überlegungen sollen nochmals anhand der fiktiven Betrachtung des Rauchverhaltens nach Geschlecht veranschaulicht werden:
Abbildung 9-1: Gegenüberstellung von Kontingez- und Indiffernztabelle zum Rauchverhalten
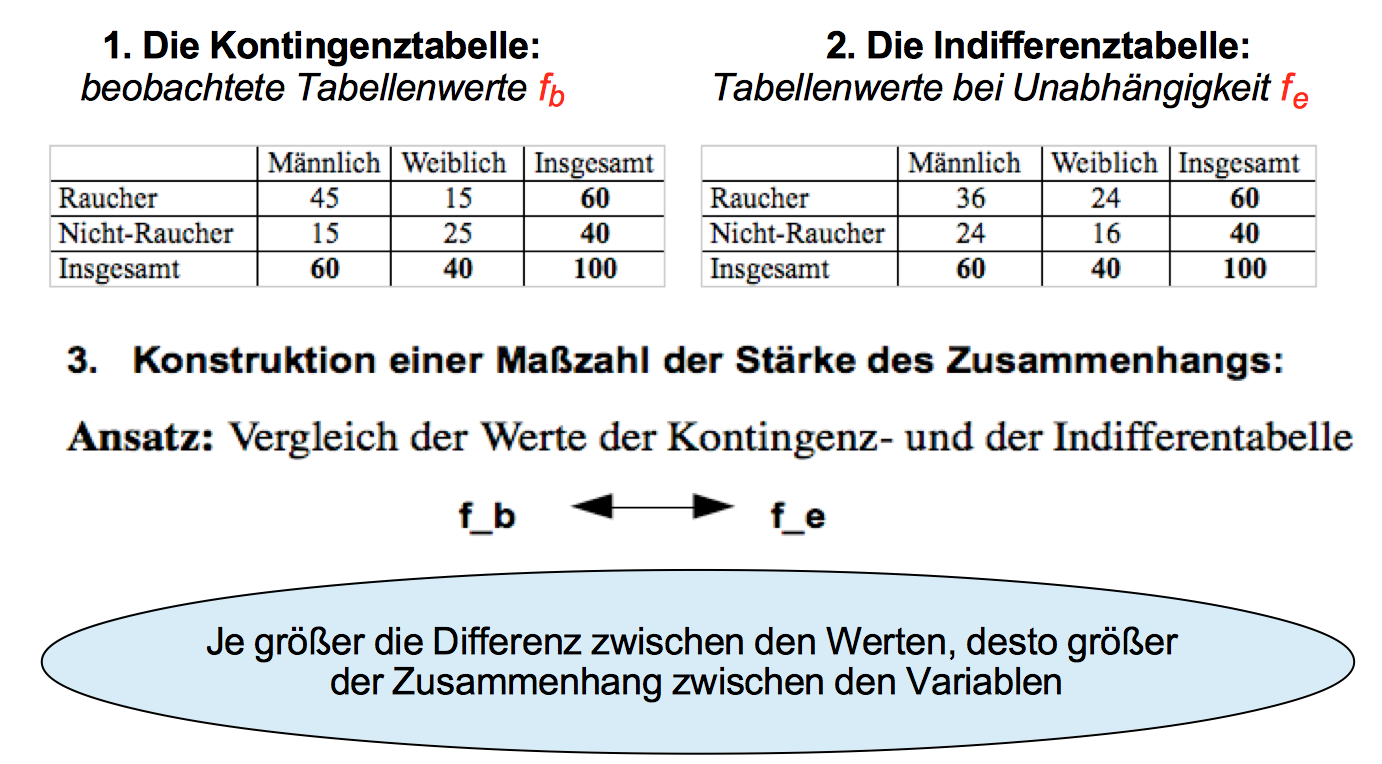
Logischerweise differieren die Werte beider Tabellenkerne umso weniger je geringer das Rauchverhalten durch das Geschlecht bestimmt ist, und umso mehr je stärker sich das Rauchverhalten der Geschlechter unterscheidet.
b) Die Formel für das χ2-Maß
Es ist also schlüssig, die Differenz (fb - fe) zwischen der Werten der Kontingenz- und der Indifferenztabelle zum Ausgangspunkt eines konstruktiven Ansatzes zu wählen.
Allerdings führt eine erste Überlegung, die Differenzen über die Tabellenfelder aufzusummieren, nicht weiter, weil sich die positiven und negativen Abweichungen gegenseitig aufheben:
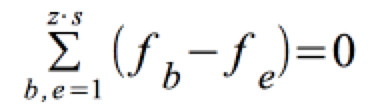
Hilfsweise werden die Differenzen quadriert, mittels einer Division durch fe relativiert und schließlich aufsummiert.
Somit lautet die Formel für Chi-Quadrat:
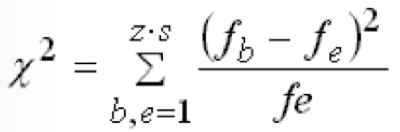
χ2 ergibt sich also als Summe der Terme 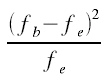 , die für jedes Feld der Kontingenztabelle berechnet werden.
Dies sei für das obige Beispiel demonstriert:
Abbildung 9-2: χ2-Wert für den Zusammenhang zwischen Geschlecht und Rauchverhalten
Eine Formel eines verkürzten Rechenverfahrens für χ2 auf der Basis einer 2 x 2 Felder-Tabelle findet sich hier
2. Die funktionalen und numerischen Eigenschaften des χ2-Maßes
a) Die funktionalen Eigenschaften von χ2
χ2 ist eine Funktion der Stärke des Zusammenhangs zwischen zwei Variablen.
χ2 lässt sich für alle Skalenniveaus berechnen.
χ2 ist unabhängig von der Richtung des Zusammenhangs.
χ2 kann Werte > 1 annehmen.
b) Die numerischen Eigenschaften von χ2
Bei Unabhängigkeit der Variablen (fb = fe) nimmt χ2 den Wert "0" an, d.h.:
0 ≤ χ2 ≤ χ2max
Aus der Formel ergibt sich, dass χ2 von der Anzahl der Beobachtungen abhängt, d.h.:
χ2 = f(N) .
Ebenso variiert χ2 mit der Tabellengröße, d.h.:
χ2 = f(Z,S).
3. Fazit
Da 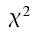 sowohl von der Fallzahl N als auch der Form der Tabelle beeinflusst wird, ermöglicht es nur tendenzielle Rückschlüsse auf die Stärke des Zusammenhanges.
Lediglich wenn 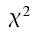den Wert Null annimmt, kann die völlige statistische Unabhängigkeit von X und Y diagnostiziert werden.
-
In der induktiven Statistik wird allerdings ein Verfahren eingeführt - der 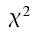-Unabhängigkeitstest - mit dem geprüft werden kann, ob ein signifikanter (mehr als zufälliger) Zusammenhang zwischen den Variablen besteht.
Im Modul IX-2 werden deshalb weitere Maßzahlen auf der Basis von 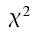vorgestellt, die Modelle für die Stärke des Zusammenhanges beinhalten und weitgehend unabhängig von Tabellenform, Tabellengröße und zahlenmäßiger Größenordnung des beobachteten Merkmals sind.
Diese Maßzahlen bewegen sich in einem Bereich zwischen 0 und 1, wobei 0 Unabhängigkeit und 1 einen vollständigen Zusammenhang bedeuten.
|
