 |
Konzepte und Definitionen im Modul VIII-2 Die statistische Unabhängigkeit
1. Statistische Modelle der (Un-)Abhängigkeit
a) Vorüberlegungen
Eindimensionale statistische Verteilungen hatten wir nicht nur tabellarisch und graphisch dargestellt, sondern auch mit statistischen Maßzahlen zur Lage beschrieben. In der zweidimensionalen statistischen Analyse haben die Maßzahlen die Aufgaben, die Stärke und u.U. auch die Richtung eines Zusammenhangs zu erfassen.
Statistische Zusammenhänge sind in der Regel stochastischer Natur, d.h. der eigentliche Zusammenhang wird durch einen Zufallsfaktor gestört, der im konkreten Fall unterschiedlich stark sein wird.
Reale, zweidimensionale Beobachtungen liegen also zwischen zwei Extremen: dem deterministischen Zusammenhang zweier Variablen, bei dem kein Zufallseinfluss zu beobachten ist, und der statistischen Unabhängigkeit zweier Variablen, bei der kein Zusammenhang feststellbar ist.
Optimal konstruierte statistische Zusammenhangsmaße sollen im ersten Fall den Wert "1" und im zweiten den Wert "0" annehmen.
b) Tabellarische und graphische Erscheinungsformen der Unabhängigkeit
Am Beispiel der zweidimensionalen Häufigkeitsverteilung der Variablen Geschlecht und Ausbildung soll überlegt werden, wie diese Tabelle aussehen müsste, wenn beide Variablen unabhängig von einander wäre.
Tabelle 8-7: Kreuztabelle - Ausbildung und Geschlecht
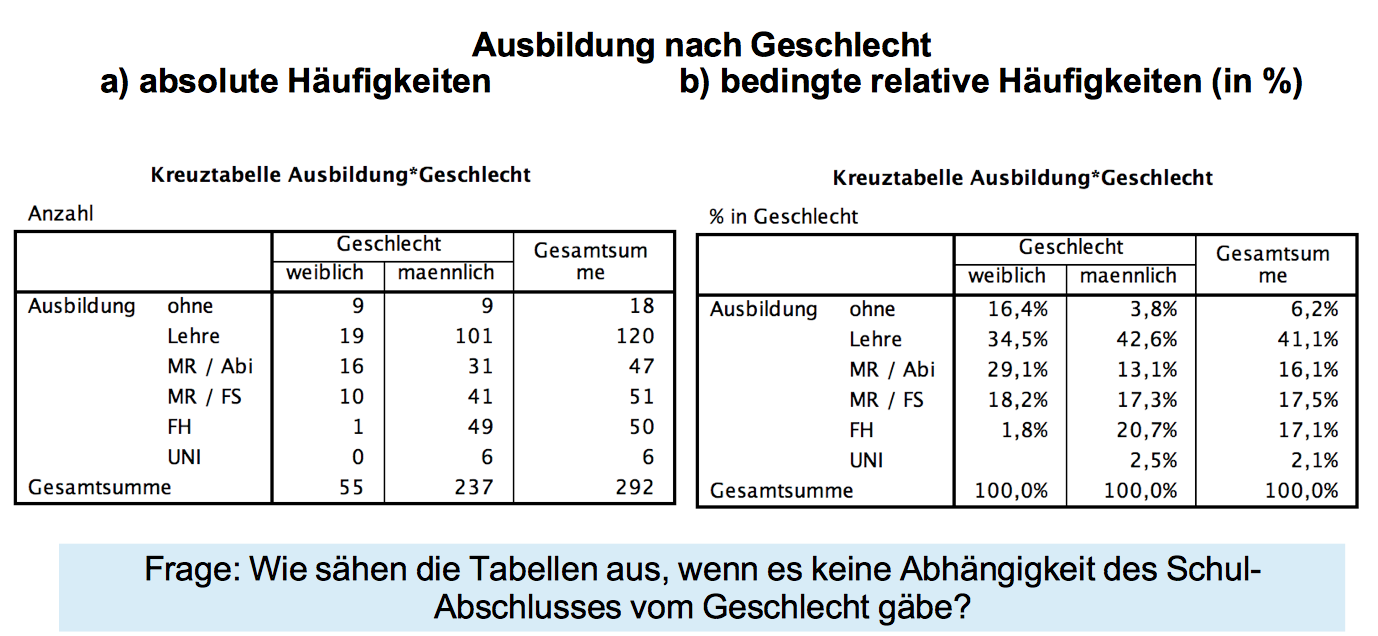
Für die linke Tabelle der absoluten Häufigkeiten ist diese Frage ohne Weiteres nicht zu beantworten. Für die rechte Tabelle schon: Bei Unabhängigkeit müssten die Prozentwerte in den beiden Spalten "weibl" und männl" den Prozenten in der Summenspalte entsprechen.
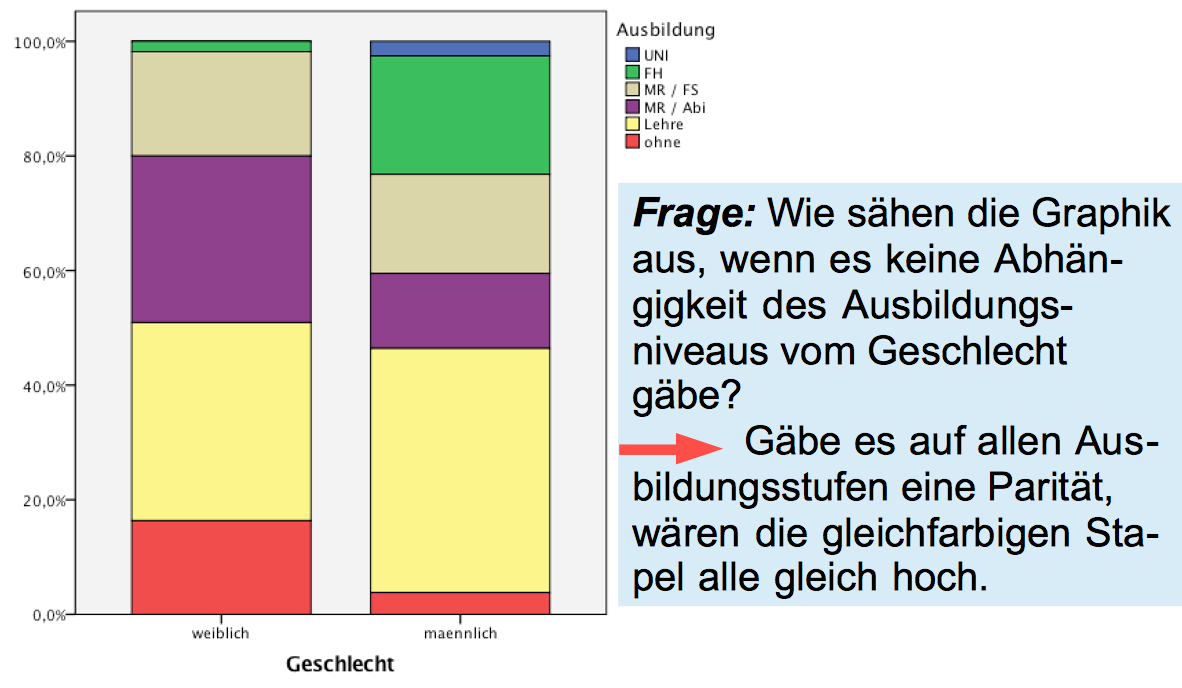
Analog ergibt sich die Antwort für das auf 100 % skalierte Säulendiagramm zu diesem Sachverhalt:
Abbildung 8-14: Säulendiagramm - Ausbildung und Geschlecht
c) Konstruktive Ansätze zur Entwicklung einer Maßzahl des Zusammenhangs
Statistische Maßzahlen der Stärke des Zusammenhangs können möglicherweise über das Ausmaß quantifiziert werden, in dem eine reale Verteilung von dem Ideal eines vollständigen Zusammenhangs bzw. einer vollständigen Unabhängigkeit abweicht. Dazu müsste die zum Vergleich dienenden die Idealverteilungen für die beobachtete Verteilung konstruiert werden. Wie dies möglich ist, wir im Folgenden an einem fiktiven Beispiel der Abhängigkeit des Rauchverhaltens vom Geschlecht demonstriert:
Beobachtetes Rauchverhalten
Tabelle 8-8: Kreuztabelle - Rauchverhalten nach Geschlecht (fiktives Beispiel)
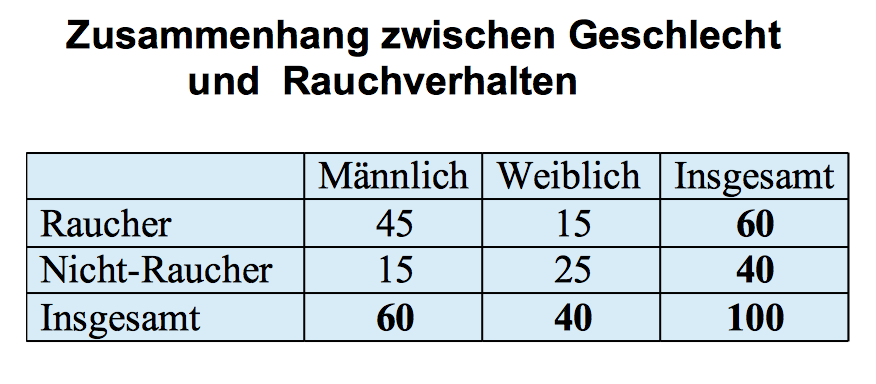
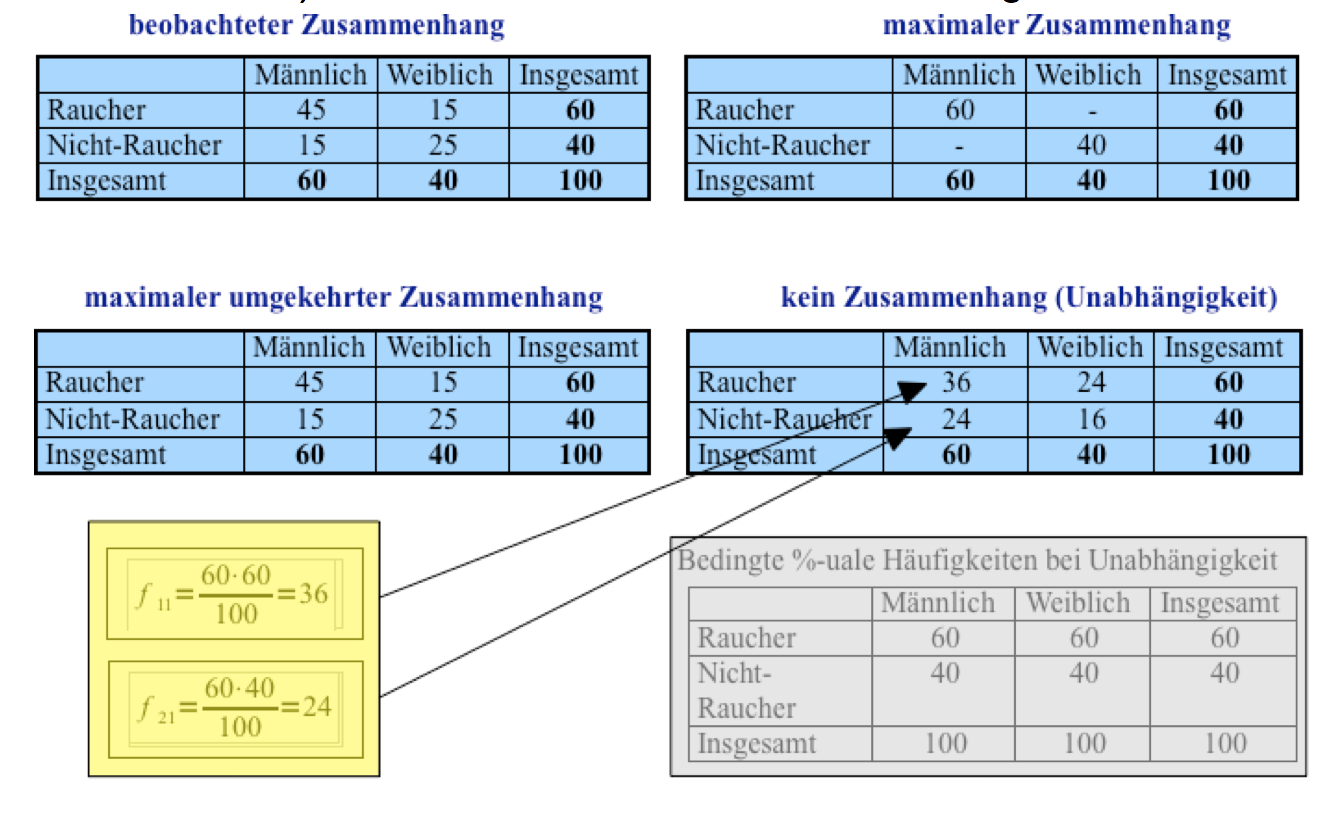
Der Tabelle ist zu entnehmen, dass die Mehrzahl der Männer raucht, während die Mehrzahl der Frauen Nichtraucherinnen sind. Rauchverhalten bei maximalem Zusammenhang
Tabelle 8-9: Maximaler Zusammenhang zwischen Geschlecht und Rauchverhalten
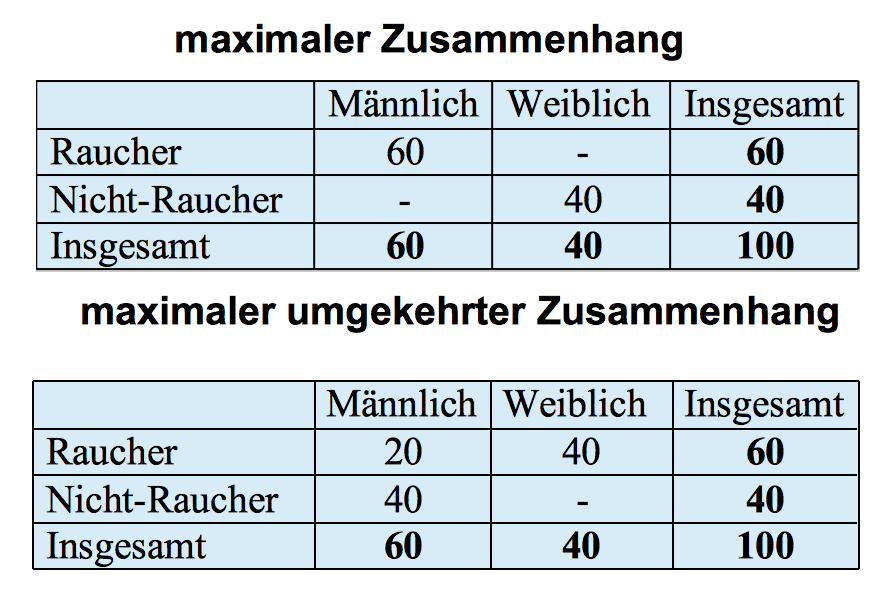
Wie man sieht, gibt es zwei Möglichkeiten eines maximalen Zusammenhangs:
-
a) alle Männer rauchen, keine Frau raucht.
-
b) alle Frauen rauchen, aber nicht alle Männer rauchen nicht. Die Häufigkeiten in den Randverteilungen erlauben für die Männer keine eindeutige Aussage über deren Rauchverhalten.
Rauchverhalten bei maximaler Unabhängigkeit
Nachdem der Bezug auf die maximale Abhängigkeit kein eindeutiges Ergebnis brachte, wird geprüft, ob die maximale Unabhängigkeit eine geeignetere Folie für eine Gegenüberstellung abgibt.
Tabelle 8-10:

In den Vorüberlegungen ergab sich, dass Unabhängigkeit dann vorliegt, wenn die prozentualen Verteilungen in den Kategorien denen der Rand-Verteilung entsprechen. Dies ist in der rechten Tabelle dargestellt.
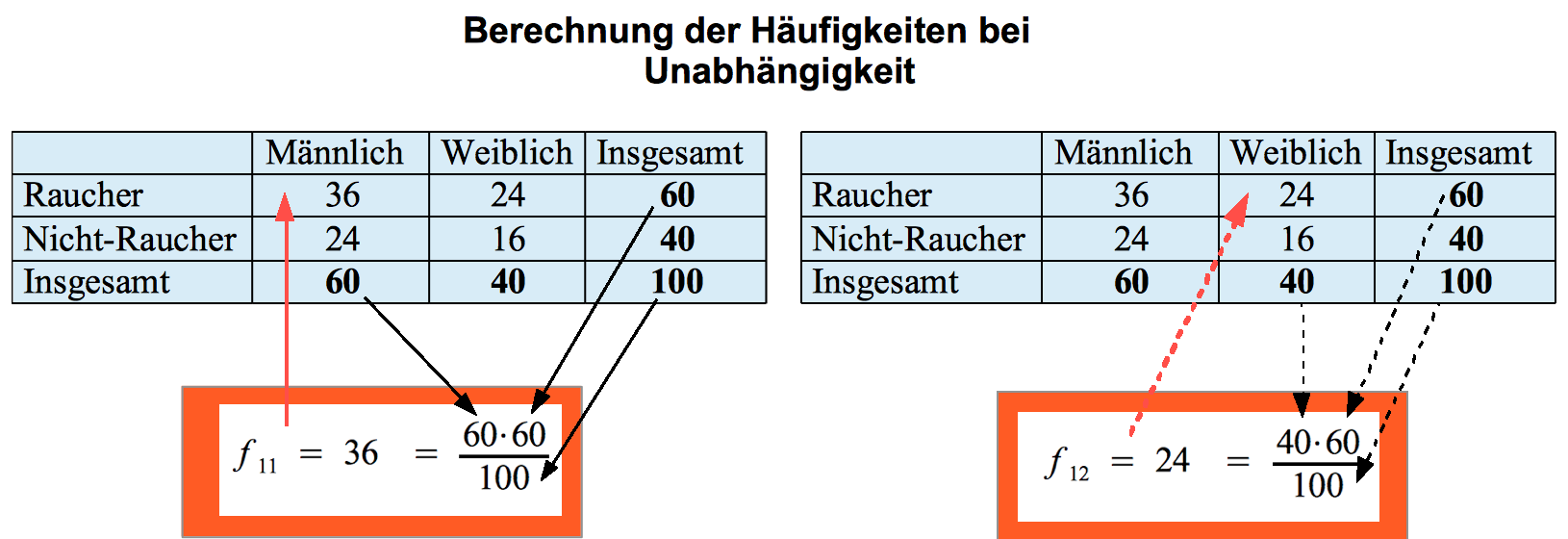
Auf dieser Basis lassen sich die bei Unabhängigkeit zu erwartenden Häufigkeiten des Rauchverhaltens für die Männer und die Frauen in der rechten Tabelle berechnen:
Berechnung des zu erwartenden Rauchverhaltens bei maximaler Unabhängigkeit
Tabelle 8-11: Berechnung der erwarteten Tabellenwerte aus den Randverteilungen
Zusammenfassung
In der folgenden Übersicht werden die Überlegungen zu den Erscheinungsformen von Abhängigkeit/Unabhängigkeit nochmals in einem Schaubild präsentiert:
Übersicht 8-1: Erscheinungsformen von Abhängigkeit/Unabhängigkeit
2. Exkurs: Sätze zur statistischen Unabhängigkeit
Auf der Basis der bisherigen Ergebnisse lassen sich die folgenden Sätze zur statistischen Unabhängigkeit formulieren:
 Sind zwei Variablen X und Y statistisch völlig unabhängig, so sind die
bedingten relativen Häufigkeiten f'(Yi|Xj)
bei gegebenem i für alle Xj gleich. Sind zwei Variablen X und Y statistisch völlig unabhängig, so sind die
bedingten relativen Häufigkeiten f'(Yi|Xj)
bei gegebenem i für alle Xj gleich.
Dies ist offensichtlich, da
bei Unabhängigkeit der Variablen die Ausprägungen der
unabhängigen Variablen eben keinen Einfluss auf die
Ausprägungen der „abhängigen“ Variablen haben.
 Sind zwei Variablen X und Y statistisch völlig unabhängig, so sind die
bedingten relativen Häufigkeiten f'(Yi|Xj)
für alle Xj gleich den einfachen relativen Häufigkeiten fi.=f(Yi) Sind zwei Variablen X und Y statistisch völlig unabhängig, so sind die
bedingten relativen Häufigkeiten f'(Yi|Xj)
für alle Xj gleich den einfachen relativen Häufigkeiten fi.=f(Yi)
Auch
dies ist an sich trivial, da bei statistischer Unabhängigkeit
die Bedingung durch die Merkmalsausprägungen der unabhängigen
Variablen keine Auswirkung auf das Auftreten der
Merkmalsausprägungen der "abhängigen" Variablen
haben.
Generell gilt: D ie
relative Häufigkeit des gemeinsamen Auftretens zweier Variablen
entspricht dem Produkt der bedingten relativen Häufigkeit des
Merkmals der einen und der einfachen relativen Häufigkeit des
Merkmals der anderen Variablen ie
relative Häufigkeit des gemeinsamen Auftretens zweier Variablen
entspricht dem Produkt der bedingten relativen Häufigkeit des
Merkmals der einen und der einfachen relativen Häufigkeit des
Merkmals der anderen Variablen
Bei Unabhängigkeit gilt: D ie
relative Häufigkeit des gemeinsamen Auftretens entspricht dem
Produkt der einfachen relativen Häufigkeiten der beiden
Variablen: fij / N = fi. / N * f.j / N ie
relative Häufigkeit des gemeinsamen Auftretens entspricht dem
Produkt der einfachen relativen Häufigkeiten der beiden
Variablen: fij / N = fi. / N * f.j / N
3. Die Konstruktion des Kontingenzmodells
a) Die Gegenüberstellung der Tabellenwerte
-
 Völlige
statistische Unabhängigkeit im Sinne dieser vier Sätze wird
in der empirischen Praxis natürlich so gut wie nie zu finden
sein. Sie stellen also noch keine ausreichende Möglichkeit dar,
Aussagen über statistische Zusammenhänge zwischen zwei
Variablen zu machen. Völlige
statistische Unabhängigkeit im Sinne dieser vier Sätze wird
in der empirischen Praxis natürlich so gut wie nie zu finden
sein. Sie stellen also noch keine ausreichende Möglichkeit dar,
Aussagen über statistische Zusammenhänge zwischen zwei
Variablen zu machen.
Das eigentlich Wichtige ist aber, dass in
Anwendung der Sätze zur stat. Unabhängigkeit jene absoluten
Häufigkeiten errechnet werden können, die bei statistischer
Unabhängigkeit zu
erwarten wären.
Der nächste logische Schritt ist
dann, zu betrachten, wie stark die empirischen Häufigkeiten von
den erwarteten Häufigkeiten abweichen und auf dieser Basis
Maßzahlen für die Stärke des Zusammenhangs zu
konstruieren.
Aus Satz 4 ergibt sich durch Multiplikation mit N:
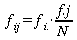 bzw. bzw.
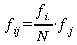
Somit lassen sich aus den Randbedingungen (den Zeilen- und
Spaltensummen) die absoluten Häufigkeiten bestimmen, die im
Falle der Unabhängigkeit der beiden Variablen zu erwarten wären.
b) Kontingenz- und Indifferenztabelle
Die Tabelle, die diese, bei Unabhängigkeit zu erwartenden Werte enthält, nennt man
Indifferenztabelle - während die Tabelle der empirisch
vorgefundenen zweidimensionalen Häufigkeitsverteilung als
Kontingenztabelle bezeichnet wird.
Zur Unterscheidung bezeichnen wir die beobachteten Häufigkeiten mit fb und die erwarteten Häfigkeiten mit fe.
Abbildung 8-15: Gegenüberstellung von Kontingenz- und Indifferenztabelle
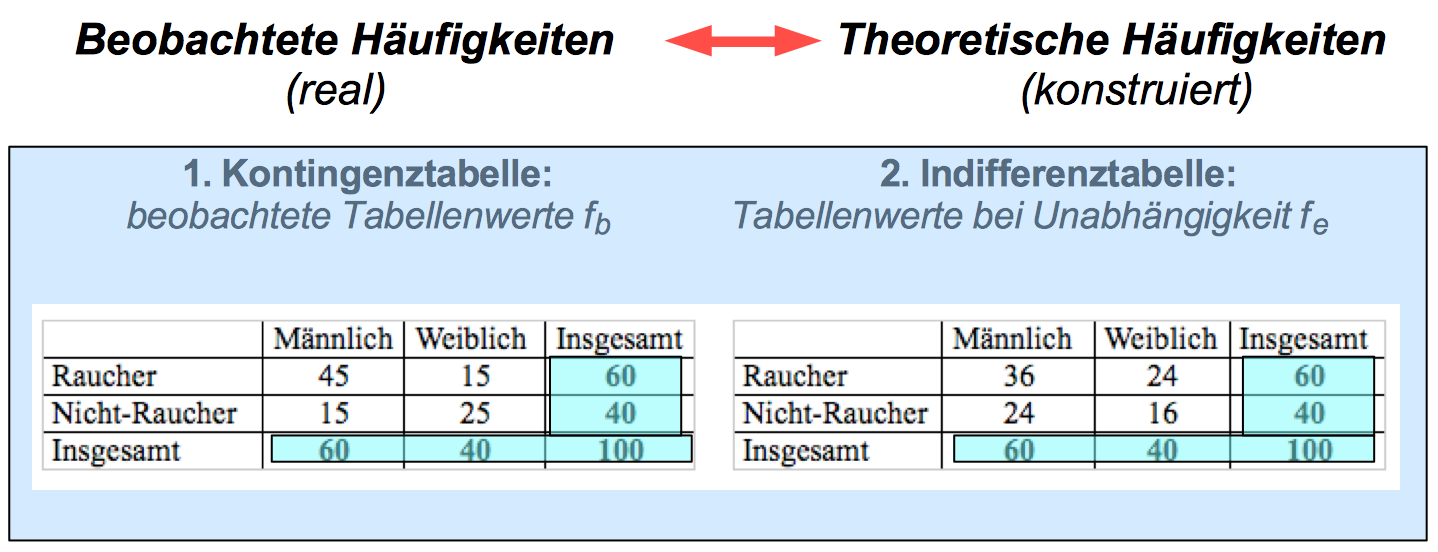
Die grün unterlegten Felder signalisieren, dass die Randverteilungen in beiden Tabellen identisch sind.
Da die fe nach der obigen Formel berechnet werden, sind im Gegensatz zur Indifferenztabelle in Abbildung 8-15 i.A. keine ganzzahligen Werte für die fe zu erwarten.
c) Die Freiheitsgrade der Indifferenztabelle
Wie man der Tabelle entnehmen kann, müssen nicht alle Felder fij nach der obigen Formel berechnet werden, den Rest erhält man als Differenz zu den Werten der Randverteilungen.
Je nach Umfang der Tabelle ergibt sich die Anzahl der originär zu berechnenden Werte über die Formel: FG=(z-1)*(s-1). FG gibt die sogenannten Freiheitsgrade einer Tabelle an.
Bei zwei Spalten und zwei Zeilen hat die Tabelle die folgenden Freiheitsgrade (FG)
FG=(z-1)*(s-1)=(2-1)*(2-1=1, also einen Freiheitsgrad. Es muss nur ein
Feld, z.B. f11= 36 nach der obigen Formel berechnet werden, die restlichen drei Felderwerte sind Differenzen zu den Werten der Summenzeile bzw. -spalte.
d) Die Konstruktion eines Zusammenhangsmaßes aus der Kontingenz- und der Indifferenztabelle
Im folgenden Kapitel IX wird gezeigt, wie man aus den Tabellenwerten der Kontingenz- und der Indifferenztabelle ein Kontingenzmaß zur Ermittlung der Stärke des Zusammenhangs zwischen zwei Variablen konstruieren kann.
|



