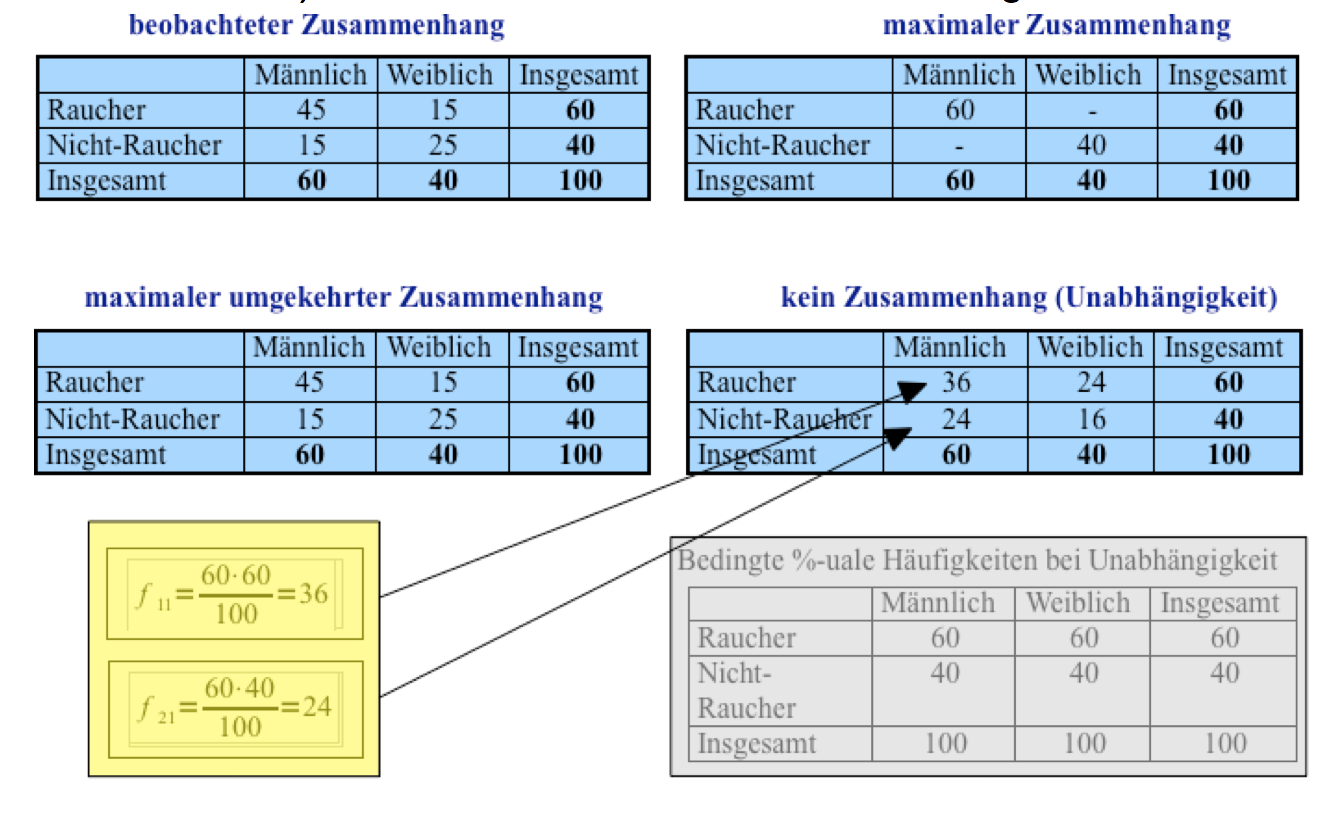
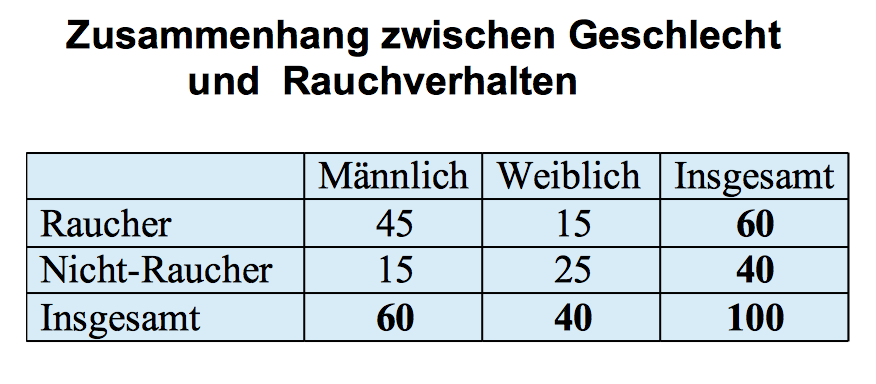
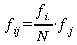Rauchverhalten bei maximalem Zusammenhang
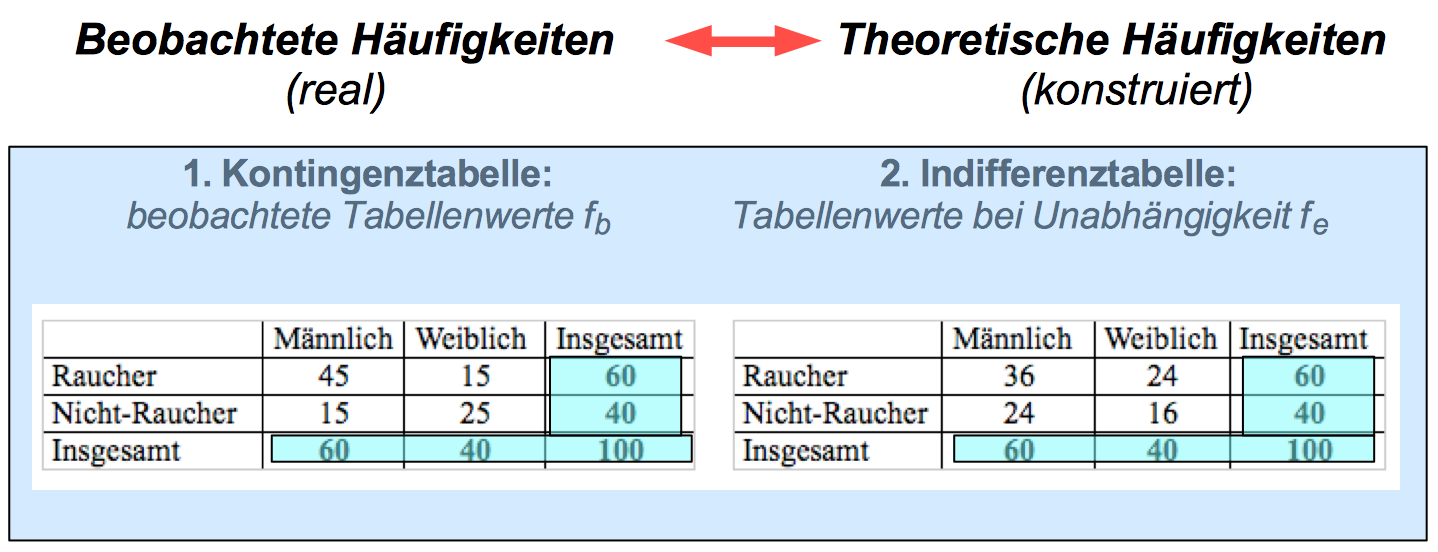
Tabelle 8-9: Maximaler Zusammenhang zwischen Geschlecht und Rauchverhalten
Wie man sieht, gibt es zwei Möglichkeiten eines maximalen Zusammenhangs:
-
a) alle Männer rauchen, keine Frau raucht.
-
b) alle Frauen rauchen, aber nicht alle Männer rauchen nicht. Die Häufigkeiten in den Randverteilungen erlauben für die Männer keine eindeutige Aussage über deren Rauchverhalten.
Rauchverhalten bei maximaler Unabhängigkeit
Nachdem der Bezug auf die maximale Abhängigkeit kein eindeutiges Ergebnis brachte, wird geprüft, ob die maximale Unabhängigkeit eine geeignetere Folie für eine Gegenüberstellung abgibt.
Tabelle 8-10:

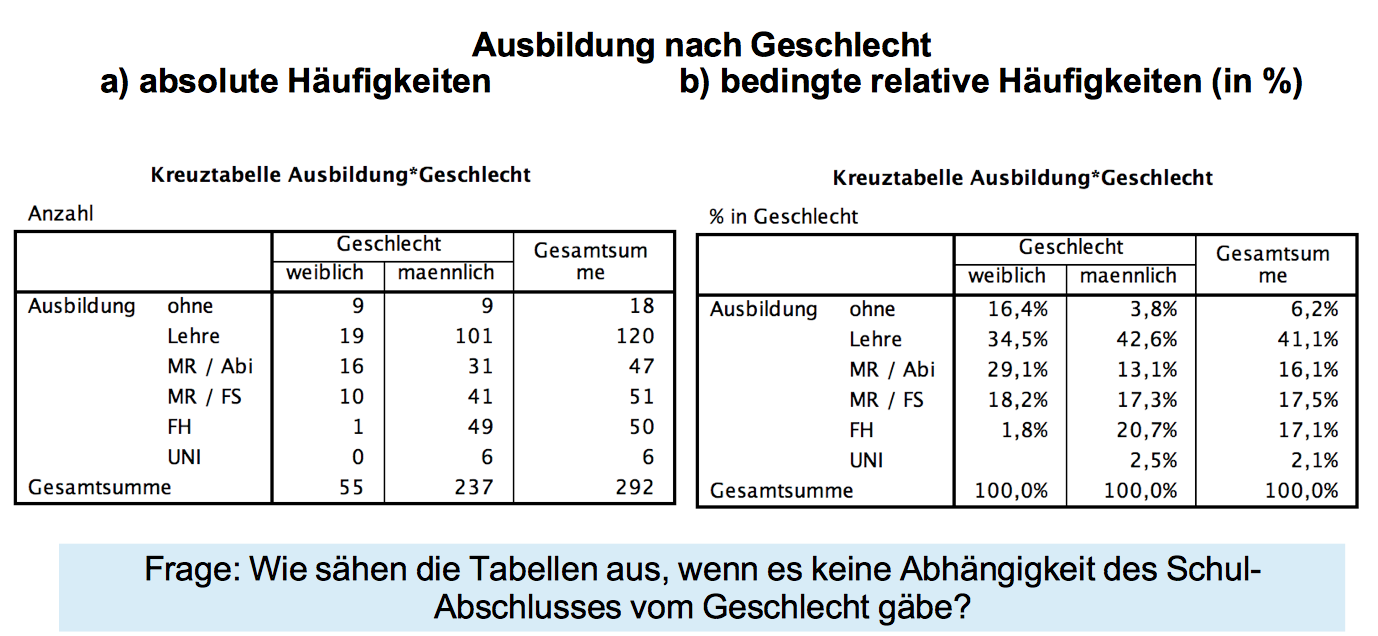
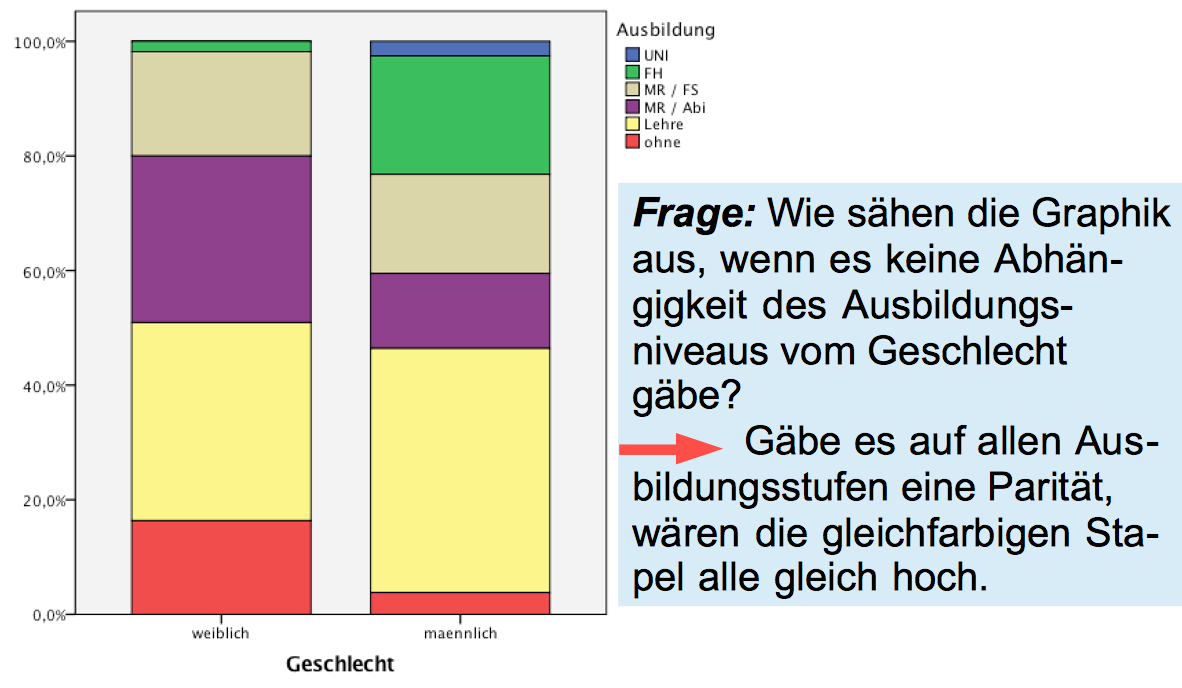
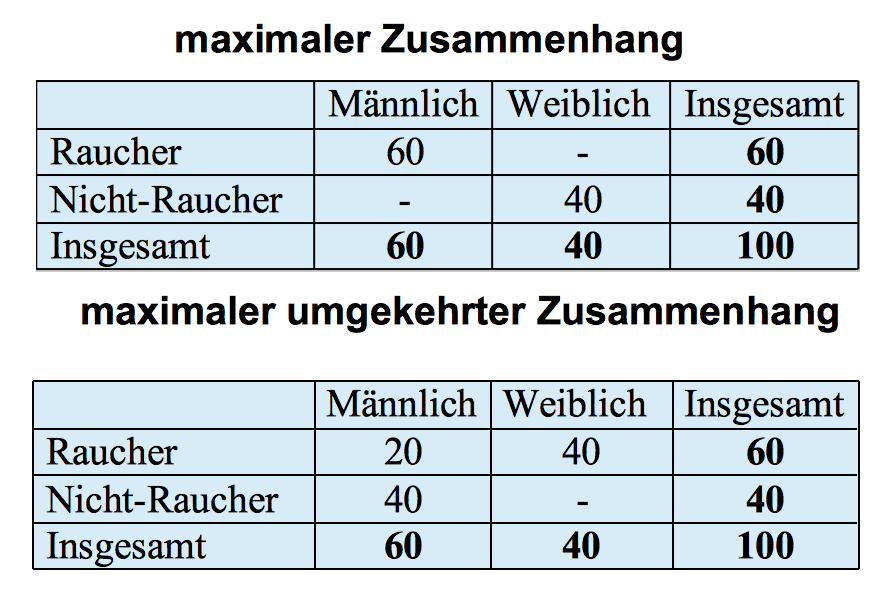
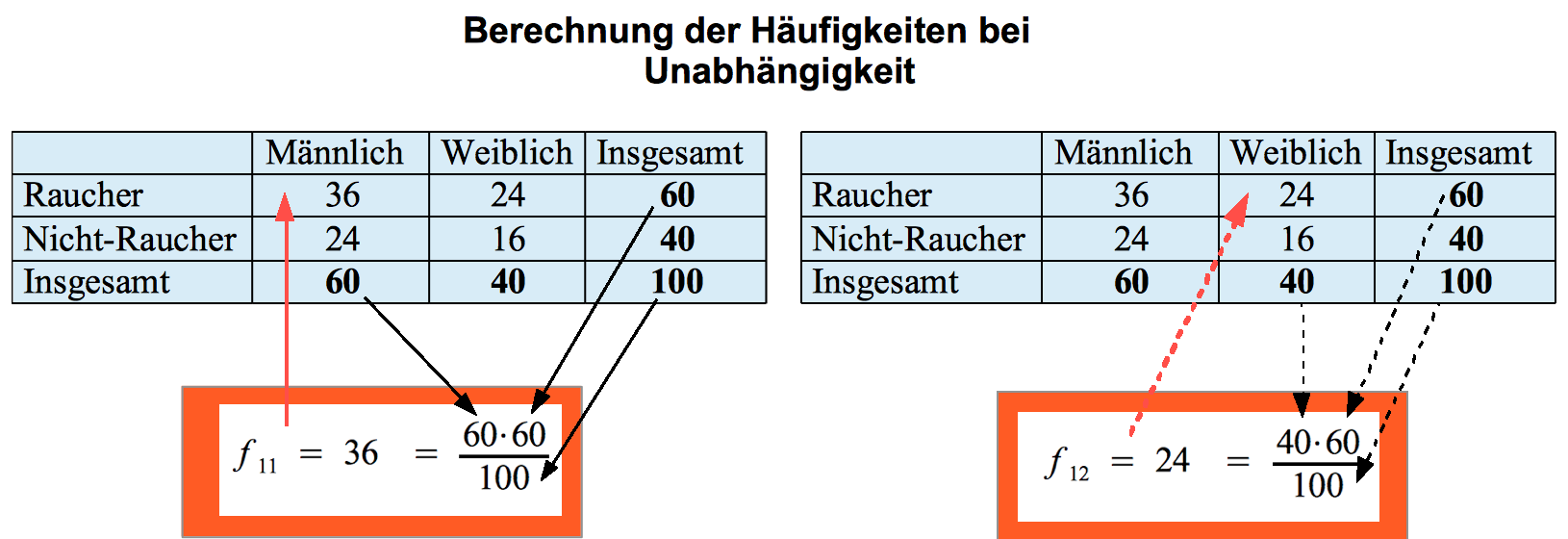
In den Vorüberlegungen ergab sich, dass Unabhängigkeit dann vorliegt, wenn die prozentualen Verteilungen in den Kategorien denen der Rand-Verteilung entsprechen. Dies ist in der rechten Tabelle dargestellt.
Auf dieser Basis lassen sich die bei Unabhängigkeit zu erwartenden Häufigkeiten des Rauchverhaltens für die Männer und die Frauen in der rechten Tabelle berechnen:
Berechnung des zu erwartenden Rauchverhaltens bei maximaler Unabhängigkeit
Tabelle 8-11: Berechnung der erwarteten Tabellenwerte aus den Randverteilungen
Zusammenfassung
In der folgenden Übersicht werden die Überlegungen zu den Erscheinungsformen von Abhängigkeit/Unabhängigkeit nochmals in einem Schaubild präsentiert:
Übersicht 8-1: Erscheinungsformen von Abhängigkeit/Unabhängigkeit