 |
Konzepte und Definitionen im Modul VIII-1 Zweidimensionale Tabellen und Graphiken
1. Tabellarische und graphische Darstellungsprinzipien
a) Die zweidimensionale Beobachtung
Eine zweidimensionale Häufigkeitsverteilung erhält man,
wenn von N Merkmalsträgern zwei verschiedene Variablen
(Merkmale) erhoben werden. Bezogen auf die Datenmatrix (vgl. Kap. II, Abb. 2-6) werden daraus zwei Spalten gemeinsam analysiert.
Jede Beobachtung i = 1...N konstituiert ein Wertepaar bzw. eine Merkmalskombination
(Xi, Yi). Dabei werden die Merkmalskategorien der unabhängigen
Variablen mit Xi und die Merkmalskategorien der abhängigen
Variablen mit Yi bezeichnet. Sofern also eine begründete
Hypothese über die Richtung eines eventuellen statistischen
Zusammenhanges vorliegt, sollte man dieser Konvention folgen.
Nach der Gruppierung oder Klassierung der Daten erhalten wir die
Wertepaare (Xj, Yi) (j = 1...s) und i = 1...z) mit den Merkmalshäufigkeiten fij.
b) Die zweidimensionale Tabelle
Eine zweidimensionale
Häufigkeitsverteilung lässt sich für alle Skalenniveaus bei einer begrenzten Zahl von Merkmalsausprägungen oder nach einer Klassierung der metrischen Merkmale adäquat in Form
der sog. Kreuztabelle darstellen (vgl. Punkt 2).
Dabei werden die Merkmalskategorien der unabhängigen
Variablen Xi üblicherweise in der Kopfzeile der Tabelle,
die Merkmalskategorien der abhängigen
Variablen Yi in der Vorspalte eingetragen (vgl. Abb. 8-1 - oben).
So kann man in der Tabelle jeweils spaltenweise von links nach rechts die Unterschiede in den Häufigkeiten der abhängigen Variablen analysieren.
c) Die zweidimensionale Graphik
Je nach Skalenniveau ergeben sich verschieden Möglichkeiten, die Tabelleninhalte graphisch zu veranschaulichen.
Für nominale und ordinale, aber auch für klassierte metrische Daten bieten sich Säulen- oder Balkendiagramme an. Diese werden nachfolgend unter Punkt 3 vorgestellt.
-
Die Wertepaare metrischer, nicht klassierter Daten können in einem Koordinatensystem, dem Streuungsdiagramm als Punktwolke präsentiert werden (vgl. Kap. XI).
Abbildung 8-1: Zweidimensionale Häufigkeitsverteilungen: Kreuztabelle und Graphiken
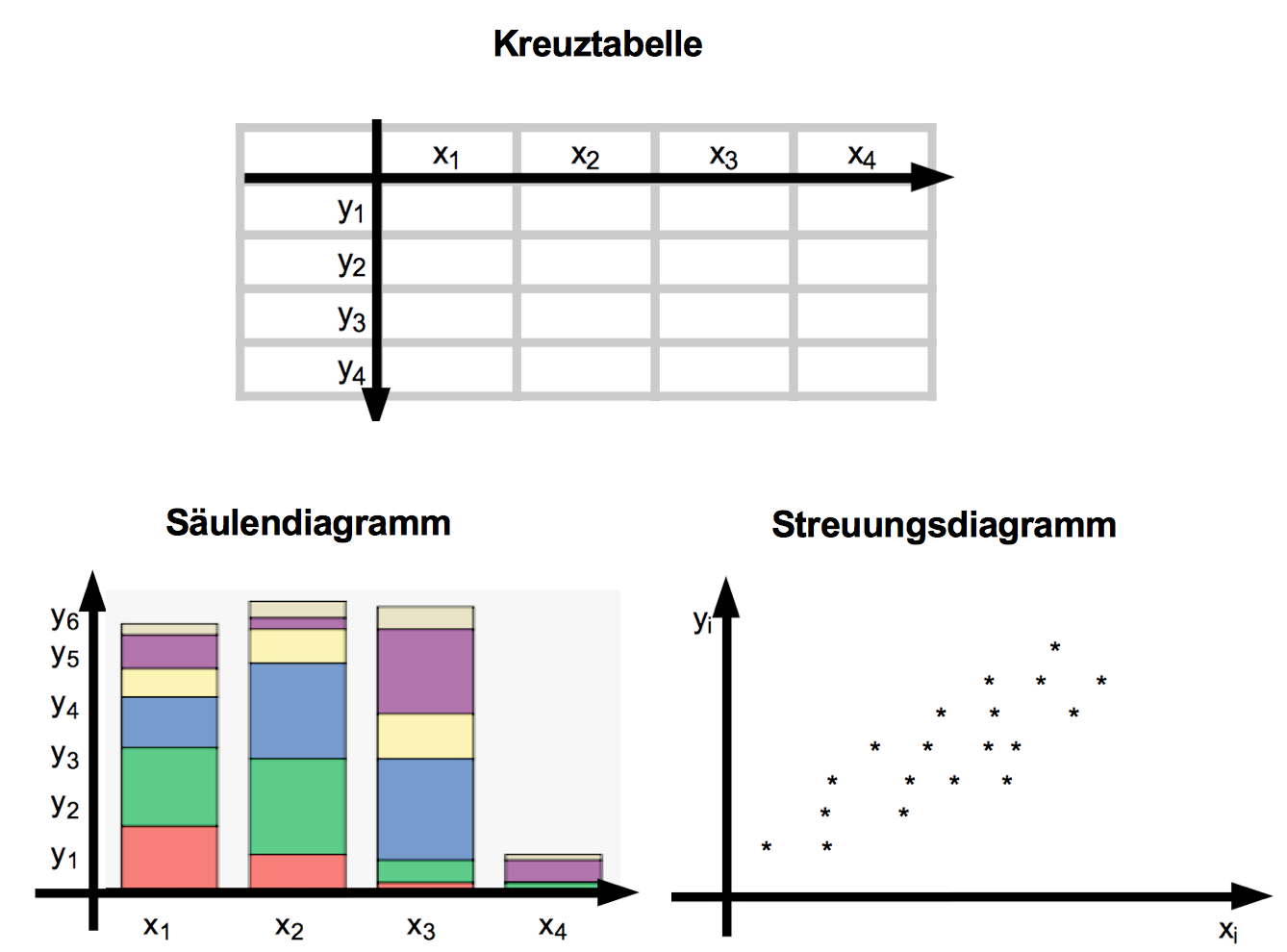
Tabellen und Graphiken unterscheiden sich in ihrer geometrischen Struktur. Während sich bei Tabellen der Koordinaten-Ursprung links oben befindet, liegt er bei den Graphiken üblicherweise links unten.
2. Die zweidimensionale Häufigkeitstabelle
a) Der Aufbau der Kreuztabelle
Die allgemeine Schreibweise einer Kreuztabelle für zwei beliebig skalierte
Variablen Xj mit j = 1....s Merkmalsausprägungen (s steht für die Anzahl der Spalten) und Yi mit i = 1....z Merkmalsausprägungen (z steht für die Anzahl der Zeilen) ist:
Tabelle 8-1 Allgemeine Form einer zweidimensionalen Häufigkeitstabelle
|
|
X1
|
X2
|
. . .
|
Xj
|
...
|
Xs
|
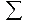
|
|
Y1
|
f11
|
f12
|
|
f1j
|
|
f1s
|
f1.
|
|
...
|
|
|
|
|
|
|
...
|
|
Yi
|
fi1
|
fi2
|
|
fij
|
|
fis
|
fi.
|
|
...
|
|
|
|
|
|
|
|
|
Yz
|
fz1
|
fz2
|
|
fzj
|
|
fzs
|
fz.
|
|
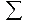
|
f.1
|
f.2
|
. . .
|
f.j
|
|
f.s
|
N
|
Die Summenspalte am rechten Rand enthält die
eindimensionale Häufigkeitsverteilung der abhängigen
Variablen, die Summenzeile am unteren Rand die
eindimensionale Häufigkeitsverteilung der unabhängigen
Variablen. Die Punkte im Index von fi. bzw. f.j symbolisieren die Ausblendung der jeweils anderen Variablen.
Die inneren Tabellenfelder fij geben die Häufigkeiten wieder, die für die Merkmalskombinationen Xi, Yi beobachtet wurden.
-
Die sog. relative Häufigkeit des gemeinsamen Auftretens
zweier Merkmalsausprägungen von X und Y erhält man durch
Division der absoluten bedingten Verteilung (grau) durch N: f'ij = fij / N
Als fiktives Beispiel
betrachten wir eine Untersuchung zur gemeinsamen Verteilung des
Geschlechts und des höchsten erreichten Schulabschlusses, deren
Ergebnis in Form der folgenden Kreuztabelle zusammengefasst wurde. In
diesem Beispiel ist klar, dass das Geschlecht nicht vom
Schulabschluss abhängen kann, also die unabhängige Variable
darstellt. Im Korpus der Tabelle sind die absoluten Häufigkeiten
der Merkmalskombinationen mit ihren Zahlenwerten aufgeführt.
Tabelle 8-2:
Zweidimensionale Verteilung von Schulabschluss und Geschlecht
|
|
Geschlecht
(Xj)
|
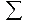
|
|
Abschluss
(Yi)
|
weiblich
|
männlich
|
|
Ohne
Abschluss
|
12
|
5
|
17
|
|
Hauptschule
|
24
|
14
|
38
|
|
Realschule
|
5
|
18
|
23
|
|
FHS-Reife
|
2
|
12
|
14
|
|
Abitur
|
3
|
5
|
8
|
|
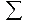
|
46
|
54
|
100
|
Eine zweidimensionale Häufigkeitstabelle der
absoluten Häufigkeiten wird sehr stark von der Größe der betrachteten Population
beeinflusst und eignet sich deshalb nicht so gut für eine
vergleichende Analyse von Zusammenhängen.
Sowohl absolute
wie relative oder prozentuale Tabellen werden
allerdings auch noch von den Besetzungszahlen der Randverteilungen
bestimmt, so dass die Strukturunterschiede (hier die
geschlechtsspezifischen Besonderheiten der Abschlusshäufigkeiten)
nur schwer zu erkennen sind. Diese Strukturunterschiede in den
jeweiligen, nach der Ursachenvariablen differenzierten
Merkmalsspalten der abhängigen Variablen lassen sich in den sog.
bedingten Verteilungen in
Form der bedingten relativen Häufigkeiten
f' ( Yi | Xj ) aufzeigen.
Ein Bild des formaler Aufbau einer zweidimensionalen Häufigkeitstabelle findet sich hier.
b) Die bedingten relativen Häufigkeiten einer abhängigen Variablen f' ( Yi | Xj)
Die inneren Tabellenfelder (in Tab. 8-3 grau markiert) enthalten die sog.
bedingte Verteilung in Form
der absoluten Häufigkeiten: fij = f(Yi | Xj) (lies: die Häufigkeit von Yi unter der Bedingung X=Xj)
Tabelle 8-3: Zweidimensionale Häufigkeiten als bedingte Häufigkeiten f' ( Yi | Xj)
|
Xj
|
|
Yi
|
x1
|
x2
|
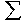
|
|
y1
|
f11=f(y1|x1)
|
f12=f(y1|x2)
|
f1.
|
|
y2
|
f21=f(y2|x1)
|
...
|
f2.
|
|
y3
|
...
|
...
|
f3.
|
|
y4
|
...
|
fi=f(y4|x2)
|
f4.
|
|
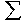
|
f.1
|
f.2
|
N
|
Die bedingten relativen Häufigkeiten ergeben sich
durch Division der inneren Tabellenfelder durch die jeweilige
Spaltensumme: f' ( Yi | Xj) = fij / f.j
Mit den bedingten relativen Häufigkeiten der Ausprägungen einer abhängigen Variablen werden die relativen Wirkungen einer bestimmten Ursachen (z.B. des Geschlechts auf den erreichten Schulabschluss) erfasst. In diesem Fall wird untersucht, wieviel Prozent der weiblichen Probanden einen Realschulabschluss aufweisen (vgl. Tab. 8-4).
Für das Beispiel der Tab. 8-2 erhalten wir:
Tabelle 8-4: Schulabschlüsse in %
nach Geschlecht (bedingte Häufigkeiten f% ( Yi | Xj)
|
|
Geschlecht
(Xj)
|
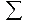
|
|
Abschluss
|
weiblich
|
männlich
|
|
Ohne
Abschluss
|
26,1
|
9,3
|
17
|
|
Hauptschule
|
52,2
|
25,9
|
38
|
|
Realschule
|
10,9
|
33,3
|
23
|
|
FHS-Reife
|
4,3
|
22,2
|
14
|
|
Abitur
|
6,5
|
9,3
|
8
|
|
|
100
|
100
|
100
|
Konkret ergibt
sich dabei aus Tab. 8-2 z. B. für das erste Feld von Tab. 8-4:
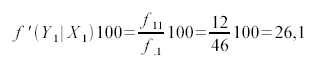
Aus den Prozentsätzen für
die einzelnen Abschlüsse ist zu erkennen, dass 38% der Beschäftigte einen Hauptschulabschluss aufweisen. Von den Frauen sind es hingegen 52,2%.
Während also fast 80% der Frauen in den beiden unteren Abschlüssen zu finden sind, weisen etwa 65% Männer mittlere und obere Abschlüsse auf.
c) Die bedingten relativen Häufigkeiten einer unabhängigen Variablen f' (Xj | Yi)
Oft ist aber auch die umgekehrte Fragestellung von Interesse, nämlich die der relativen Relevanz einer Ursache für eine beobachtete Wirkung. Mit der bedingten relativen Häufigkeiten der unabhängigen Variablen ist z.B. zu klären, wieviel Prozent der Realschulabsolventen weiblich sind.
Dazu ist es notwendig, die Ausgangstabelle (Tab. 8-1 bzw. Tab. 8-2) zeilenweise auf die Summenspalte zu prozentuieren.
Tabelle 8-5:
Zweidimensionale Verteilung von Schulabschluss und Geschlecht (bedingte relative Häufigkeiten f% ( Xj | Yi)
|
|
Geschlecht
(Xj)
|
|
|
Abschluss
(Yi)
|
weiblich
|
männlich
|
|
Ohne
Abschluss
|
70,6
|
29,4
|
100
|
|
Hauptschule
|
63,2
|
36,8
|
100
|
|
Realschule
|
21,7
|
78,2
|
100
|
|
FHS-Reife
|
16,7
|
83,3
|
100
|
|
Abitur
|
37,5
|
62,5
|
100
|
|
|
46,0
|
54,0
|
100
|
Der Aufbereitung der Daten in Tab. 8-5 lässt sich entnehmen, dass 46% der Belegschaft Frauen sind, diese aber in der Personengruppe ohne Schulabschluss zu 70,6 % vertreten sind.
Der Anteil der Männer beträgt insgesamt 54%, unter den Belegschaftsmitgliedern mit FHS-Reife sind sie jedoch mit 83,3% überrepräsentiert.
3. Die graphische Darstellung zweidimensionaler Häufigkeitsverteilungen
a) Konstruktionsprinzipien für Säulen- resp. Balkendiagramme
Tabellierte zweidimensionale Häufigkeitsverteilungen lassen sich durch
Säulen- oder Balkendiagramme visualisieren. Diese unterscheiden sich hinsichtlich eines vertikalen oder horizontalen Verlaufs der Stäbe:
Abbildung 8-2: Balkendiagramm und Säulendiagramm
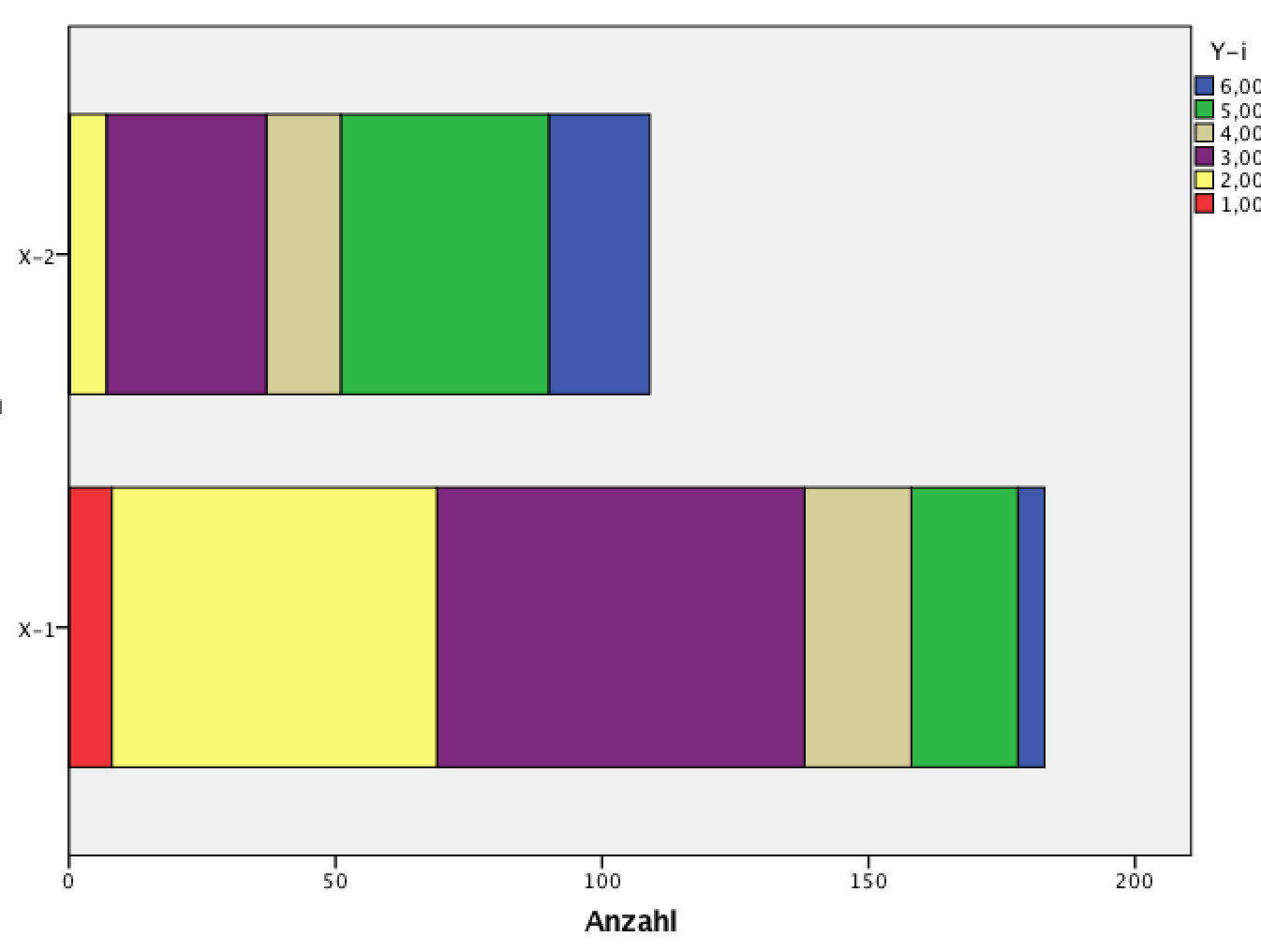 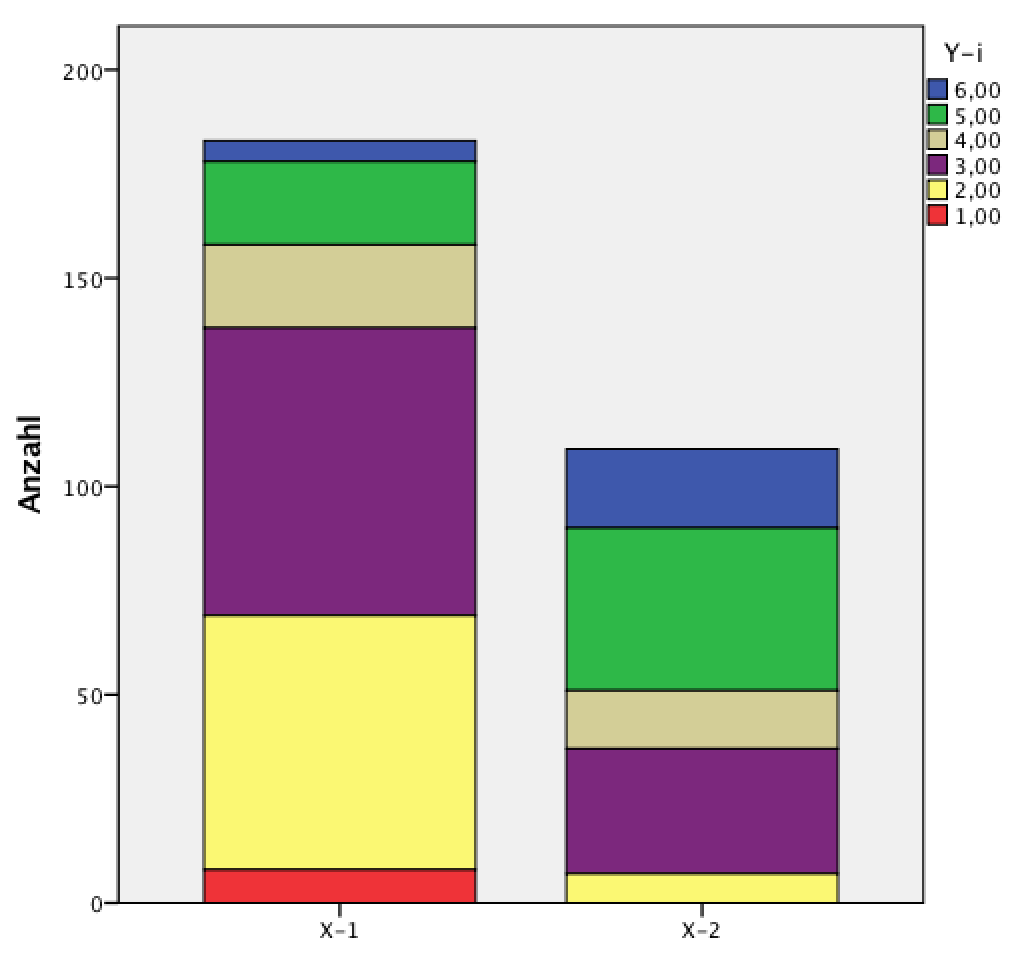
Manchmal werden aber auch vertikale Säulendiagramme sprachlich ungenau als Balkendiagramme bezeichnet (so z.B. in SPSS).
Bei der Wahl zwischen den beiden Darstellungsformen des Diagramms sind zwei Aspekte zu berücksichtigen:
Zum einen die Zielsetzung der Darstellung, zum anderen die Korrespondenz mit einer ev. ebenfalls präsentierten Kreuztabelle.
Steht die korrekte graphische Wiedergabe der beobachteten Häufigkeiten der Kreuztabelle im Vordergrund, werden die Werte der absoluten Häufigkeiten der Tab. 8-1 bzw. 8-2 in gruppierten oder in gestapelten Säulendiagrammen veranschaulicht, weil das Säulendiagramm die Zeilen- und Spaltenanordnung der Kreuztabelle adäquat wieder gibt.
Soll der Einflusses oder die Wirkung der unabhängigen Variable herausgearbeitet werden, bezieht man sich besser auf die Werte der bedingten relativen Häufigkeiten (vgl. Tab. 8-4 bzw. 8-5). In diesem Fall wird das gestapelte Balken- bzw. Säulendiagramm auf 100% skaliert.
Werden die Tabellendaten spaltenweise in bedingte relative Häufigkeiten der abhängigen Variablen umgerechnet, um den Einfluss der unabhängigen Variablen herauszuarbeiten, werden diese %-Werte adäquat mit einem Säulendiagramm visualisiert.
Soll hingegen zeilenweise die prozentuale Verteilung der unabhängigen Variablen in den Kategorien der abhängigen Variablen analysiert werden, bietet sich das Balkendiagramm an.
Beim Balkendiagramm wird die unabhängige Variable X auf der Vertikalen abgetragen. Die horizontale Achse skaliert die beobachteten Häufigkeiten der einzelnen Kategorien der abhängigen Variablen Y (vgl. Abb. 8-2 links).
Beim Säulendiagramm wird die unabhängige Variable X auf der Horizontalen abgetragen. Die Vertikale (Y-Achse) skaliert die beobachteten Häufigkeiten der einzelnen Kategorien der abhängigen Variablen Y (vgl. Abb. 8-2 rechts).
Bei ordinal- und metrisch-skalierten Y-Variablen - bei denen die Merkmalsreihenfolge relevant ist - gibt es zwei Optionen für die Anordnung der Kategorien:
Eine Reihung der Werte von unten nach oben in aufsteigender Weise (wie in Abb. 8-2) entspricht dem Prinzip des Koordinatensystems mit dem Nullpunkt links unten, d.h. die jeweils kleinste Merkmalsausprägung definiert den den untersten Stapel, die jeweils größte beschließt die Säule nach oben. Steht die Graphik für sich, sollte sie dem Koordinatenverlauf entsprechen (vgl. dazu nochmals Abb. 8-1).
Umgekehrt entspricht eine Reihung der Werte von oben nach unten in aufsteigender Weise der Reihung der Werte in der Tabelle (mit dem Nullpunkt link oben). Dient also die Graphik zur Veranschaulichung der Tabelle, sollten sich die Reihungen entsprechen, d.h. die jeweils größte Merkmalsausprägung einer Säule bzw. eines Balken definiert den 1. Stapel, die jeweils kleinste Ausprägung den letzten Stapel.
Im Folgenden wird vorwiegend mit Säulendiagrammen und der entsprechenden Bezeichnung (auch bei SPSS-Präsentationen) gearbeitet. Ein Beispiel für gestapelte und skalierte Balkendiagramme findet sich im folgenden Arbeitsschritt "Beispiele und Aufgaben".
b) Das gruppierte Säulendiagramm
In diesem Diagramm werden die bedingten Verteilungen der Variablen Y für die verschiedenen Kategorien der Variablen X , d.h. die f(Yi | Xj) dargestellt. Dabei drücken die Höhen
der Säulen die Besetzungszahlen fij der nach den Kategorien gruppierten Beobachtungen aus:
Abbildung 8-3: Das gruppierte Säulendiagramm
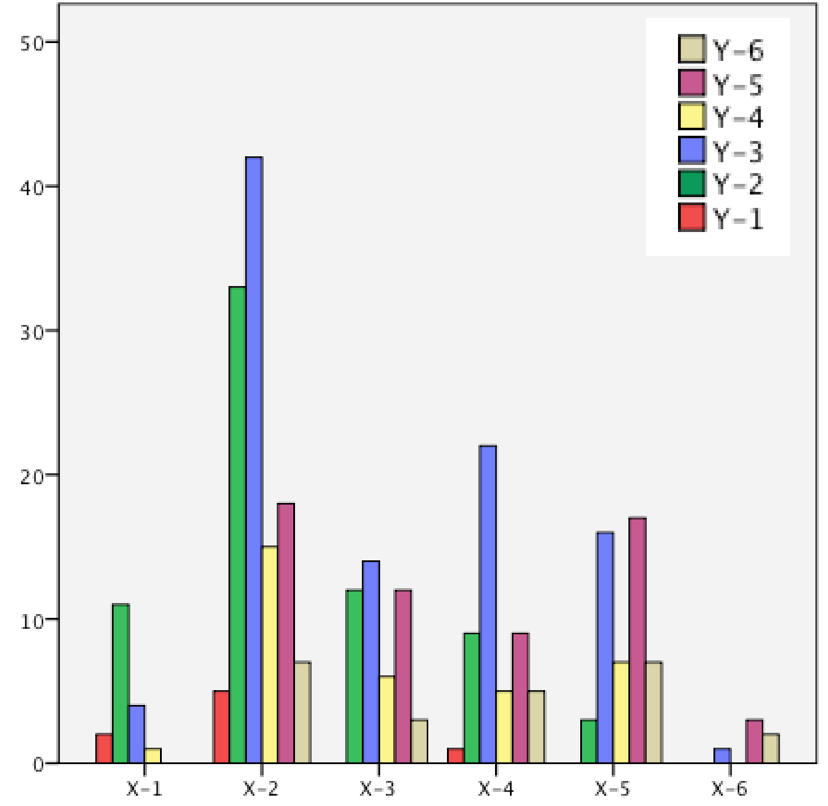
Im Diagramm wird deutlich, dass die Kategorie X2 am stärksten besetzt ist und dass darin das Merkmal Y3 die größte Untergruppe darstellt.
Insgesamt jedoch erscheint bei gleichem Informationsgehalt das nachfolgende, gestapelte Säulendiagramm übersichtlicher.
Anmerkung: In der von SPSS im Programm Kreuztabellen angebotenes gruppiertes Diagramm wird die bedingte Verteilung der f(Xj | Yi) dargestellt. Das heißt, dass anders als in Abb. 8-3 auf der Abszisse die Y i aufgetragen sind (vgl. dazu Modul VIII-3).
c) Das gestapelte Säulendiagramm
Wie im gruppierten Säulendiagramm werden die Häufigkeiten in der Höhe der Einzel-Säulen wiedergegeben. Diese stehen aber nicht nebeneinander, sondern sind aufeinander gestapelt.
Abbildung 8-4: Das gestapelte Säulendiagramm
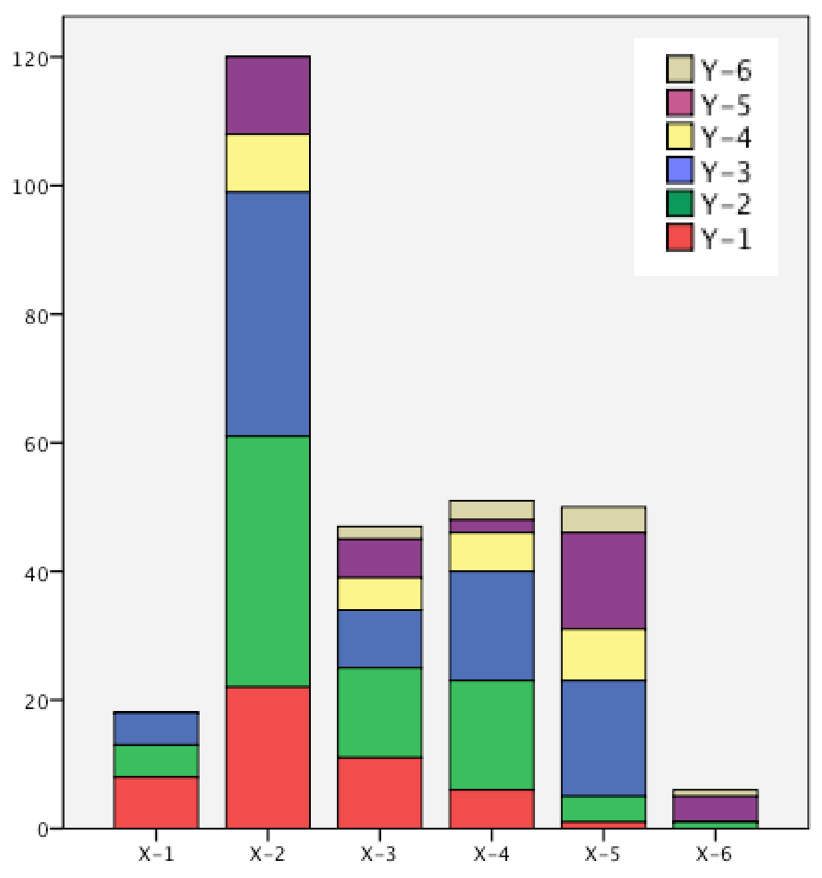
In diesem Diagramm werden die Größenverhältnisse in den Xj-Kategorien unmittelbar ersichtlich, während sich die innere Struktur der Yi nur schwer erschließt (vgl. dazu Abb. 8-6).
Da der Abbildung 8-4 die selben Größenverhältnisse der Säulen wie in Abb. 8-3 zugrunde liegen und das gestapelte Säulendiagramm anschaulicher ist, wird es im Folgenden dem gruppierten Diagramm vorgezogen.
Für das praktische Beispiel der Schulabschlüsse nach Geschlecht (vgl. Tab. 8-2) ergeben sich zwei Säulen für die
beiden Geschlechtergruppen. Die Segmentierungen der Säulen folgt aus
den Häufigkeiten der beiden Spalten im Tabellenkern. Beim
Säulendiagramm ist zu beachten, dass die Ausprägungen für
das Merkmal „Ausbildungsabschluss“ im Gegensatz zur
Tabelle von unten nach oben aufgeführt sind.
Abbildung 8-5:
Schulabschlüsse nach Geschlecht (abs. Häufigkeiten)
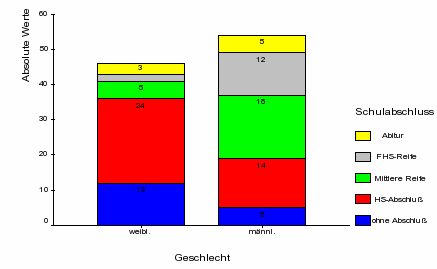
Obwohl die Geschlechterproportionen in etwa gleich sind, lassen sich die
geschlechtsspezifischen Besonderheiten der Abschlusshäufigkeiten nur ungefähr erkennen.
Unmittelbarer jedoch kommt dieser Sachverhalt in
Säulendiagramm der bedingten prozentualen Häufigkeiten (vgl. Abb. 8-7) zum
Ausdruck.
d) Das auf 100% skalierte gestapelte Säulendiagramm
Die bedingten Verteilungen lassen sich in absoluter oder relativer Form als gestapelte, auf 100% skalierte Säulendiagramme graphisch darstellen.
Die auf 100% skalierte Abb. 8-4 ist im folgenden Diagramm wiedergegeben:
Abbildung 8-6: Auf 100% skaliertes gestapeltes Säulendiagramm
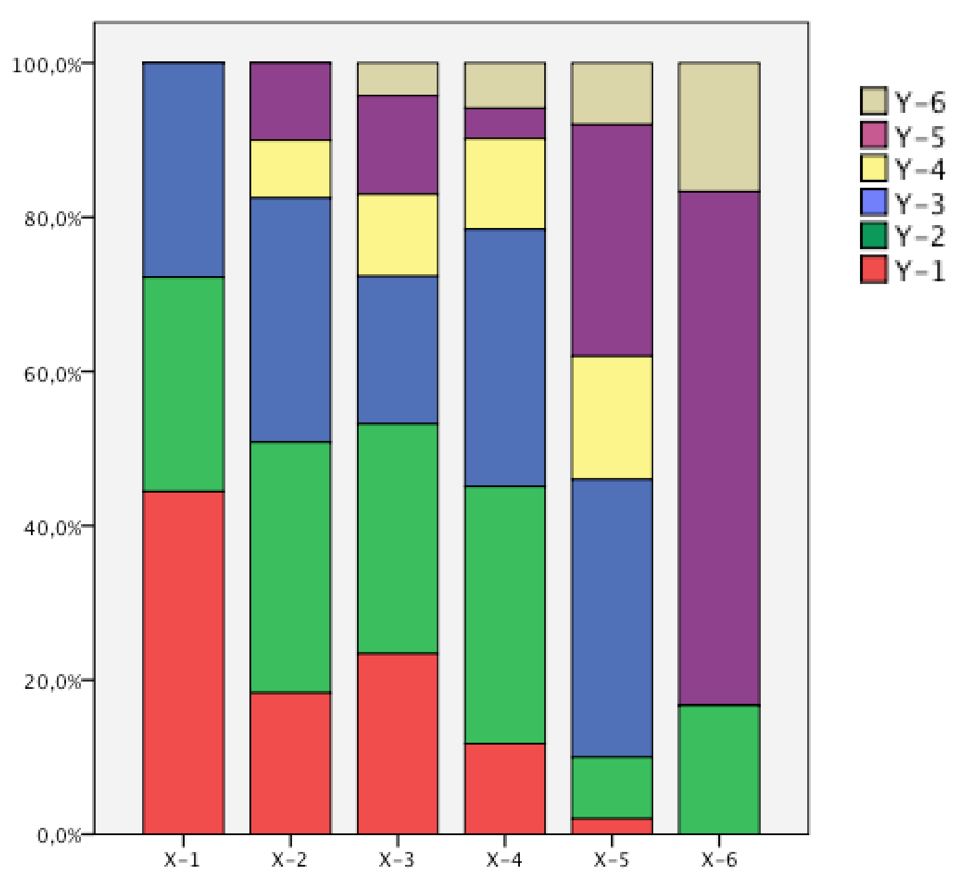
Durch die Skalierung lassen sich die Zusammenhänge zwischen den beiden Variablen klar herausarbeiten. So nehmen die Anteile der Kategorien Y1 - Y3 mit zunehmendem Xj deutlich ab, die der Kategorien Y5 und Y6 deutlich zu. Die Kategorie Y4 ist nur im Bereich X2 bis X3 vorzufinden.
Die bedingten Häufigkeiten des Schulabschlusses nach Geschlecht in Abb. 8-7 veranschaulichen die Daten aus Tab. 8-4:
Abbildung 8-7: Säulendiagramm
der Schulabschlüsse nach Geschlecht (bedingte Häufigkeiten in %)
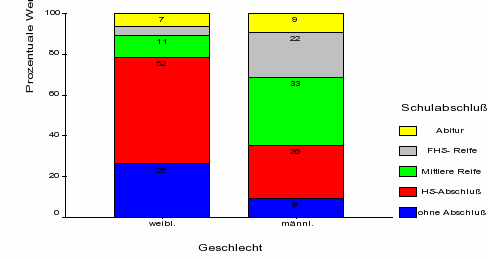
Den Einfluss des Geschlechts auf den Schulabschluss in dieser fiktiven Population bringt dieses skalierte Säulendiagramm deutlich zum Ausdruck. So verfügen fast 80% der weiblichen Mitglieder maximal über einen Hauptschulabschluss, wohingegen etwa 70% der männlichen Bevölkerung einen Abschluss darüber aufweisen.
|



