1.Vorbemerkung

• Gini-Koeffizient und Lorenzkurve sind geeignete Darstellungsformen für Konzentrationsprozesse innerhalb einer Population, deren Umfang durch den Prozess selbst nicht unmittelbar beeinflusst wird. Bei Konzentrationsprozessen unter den Anbietern auf einem Markt können Konkurrenten vom Markt ausgeschlossen werden, so dass die Anzahl der Anbieter sinkt.

• Die Notwendigkeit eines zusätzlichen Modellansatzes kann an folgendem einfachen Beispiel veranschaulicht werden: Auf einem Gütermarkt seien zum Zeitpunkt t₀ 8 Anbieter vertreten, um denen die größten vier einen Marktanteil von 80% auf sich vereinen und die übrigen sich den Rest aufteilen (vgl. Tab. 6-5). Der Gini-Koeffizient würde in diesem Fall eine gewisse Konzentration signalisieren. Zum Zeitpunkt t₁ seien die kleinen Anbieter vom Markt verdrängt und die vier größten würden den Markt gleichmäßig unter sich aufteilen. Dies würde wegen der gleichen Verteilung zu einem Gini-Koeffizienten von "0" führen, d.h. nach dem bisherigen Konzept läge nun überhaupt keine Konzentration mehr vor.

• Mit den statistischen Modellen der absoluten Konzentration werden nun nicht nur die Veränderungen der Marktanteile unter den Anbietern, sondern auch die Konzentration auf weniger Anbieter darstellbar. Zur Umsetzung des Modells der absoluten Konzentration gibt es verschiedene Konzepte.

2. Die Konzepte der absoluten Konzentration

a) Die Konzentrationsrate

• Das einfachste Modell der absoluten Konzentration bezieht sich auf die Summe der Anteile h_i der r größten Merkmalsträger an der Merkmalssumme. Dabei wird r i.A. gleich 3, 4, 5, 10, 20 oder 100 gewählt. Dazu werden die Anbieter der absoluten Größe nach bzw. ihrer relativen Anteile an der Merkmalssumme nach geordnet.

• Als Merkmale X_i können den Konzentrationsanalysen produzierte Mengen, getätigte Umsätze, Beschäftigtenzahlen, Bilanzsummen o. ä. zugrunde gelegt werden.

• Das Modell der absoluten Konzentration soll im Folgenden anhand des o.a. fiktiven Beispiels der Marktanteile h_i von r Anbieter erörtert werden (vgl. Tab. 6-5).

  Tabelle 6-5: Marktanteile h_i von r Anbietern zu den Zeitpunkten t₀ und t₁

  	Anbieter i
  Nr.	1	2	3	4	5	6	7	8
  t0	0,2	0,2	0,2	0,2	0,05	0,05	0,05	0,05
  t1	0,25	0,25	0,25	0,25	-	-	-	-

• Die Konzentrationsrate

  
  
  

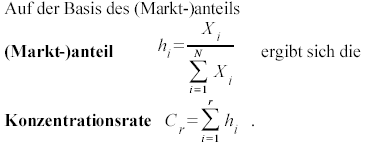
  Diese beträgt bei r = 4 für das obige Beispiel zu t₀ "0,8" und zu t₁ "1,0"; die Konzentration hat also eindeutig zugenommen.

• C_r ist zwar einfach zu berechnen und zu interpretieren, hat aber den Nachteil, dass Konzentrationsprozesse innerhalb der r Merkmalsträger nicht erfasst werden.

b) Die Konzentrationskurve

• Die Konzentrationsprozesse innerhalb der r Merkmalsträger lassen sich graphisch mittels der Konzentrationskurve darstellen. Dies soll ebenfalls an obigem Beispiel erläutert werden.

• Die Konzentrationskurve stellt die aufkumulierten Merkmalsanteile 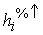dar, die über die Anbieter i = 1...r betrachtet werden. In Abb. 6-3 sind die Marktstrukturen zu den beiden Zeitpunkten t₀ und t₁ dargestellt:

  Abbildung 6-3: Konzentrationskurven zu t₀ und t₁

  

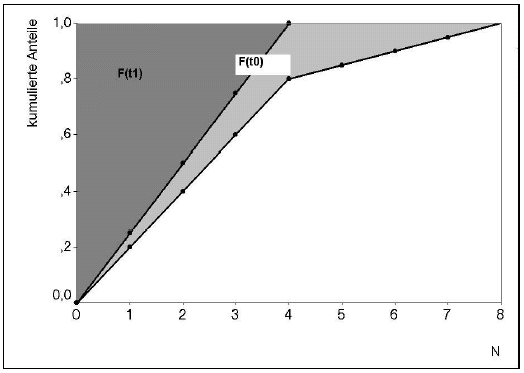
  In der Abbildung wird deutlich, dass die Kurve umso flacher verläuft, je gleichmäßiger die Marktanteile sind und die Fläche F über der Kurve umso kleiner wird, je größer die Konzentration ist. Im Beispiel ist F(t₁)<F(t₀).

• Die graphischen Ausdrücke unterschiedlicher Marktstrukturen in Abb. 6-3 lassen sich rechnerisch durch den Rosenbluth- oder den Herfindahl-Index quantifizieren.

c) Der Rosenbluth-Index

• Da die Größe der Fläche F über der Kurve in einem umgekehrten Verhältnis zur Stärke der Konzentration steht, wird sie im Rosenbluth-Index C_R in das folgende Verhältnis zum Index gesetzt:

  

• Die Ergebnisse besagen, dass die Marktkonzentration zugenommen hat, wenngleich sie, trotz der geringen Anzahl von Anbietern, aufgrund der gleichmäßigen Aufteilung des Marktes als insgesamt eher noch gering zu beziffern ist. Werte nahe bei "1" ergeben sich diesem Ansatz zufolge erst bei fast schon monopolistischen Marktverhältnissen.

d) Der Herfindahl-Index

• Der zweite Ansatz, der Herfindahl-Index C_H beruht ebenfalls auf den Marktanteilen h_i, diese werden aber quadriert und über die Marktteilnehmer aufsummiert:

  
  

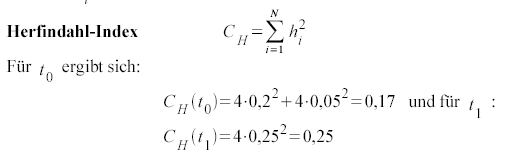
• Damit fallen die Ergebnisse für den Herfindahl-Index im Beispiel fast in den gleichen Wertebereich wie für den Rosenbuth-Index.

• 
  [1] Zu den Einzelheiten des Ansatzes und zur Ableitung der Formel, vgl. Litz 3. Aufl., S. 115 ff.

  ---

  Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 4 Benutzern im Durchschnitt mit "gut" bewertet.

  1/2 50 % Fortschritt

   

| Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächster Arbeitsschritt |