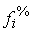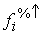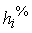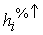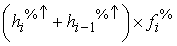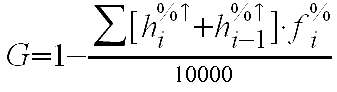| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Konzepte und Definitionen im Modul VI-1 Die relative Konzentration
1. Das Konzept der relativen Konzentration
Das Konzept der relativen Konzentration ist das geeignete Modell zur Erfassung von Konzentrationsprozessen innerhalb einer Population, deren Umfang durch den Prozess selbst nicht unmittelbar beeinflusst wird. So hat z. B. die Verteilung einer Menge von Konsumgütern oder der Vermögen über die privaten Haushalte eines Landes keinen Einfluss auf die Anzahl der Haushalte selbst.
Bei Konzentrationsprozessen unter den Anbietern auf einem Markt können Konkurrenten vom Markt ausgeschlossen werden, so dass die Anzahl der Anbieter sinkt. Die Notwendigkeit eines zusätzlichen Modellansatzes für zum Konzept der absoluten Konzentration, das im nächsten Modul vorgestellt wird.
Mit der relativen Konzentration betrachten wir die Verteilung der Merkmalssumme ∑ Xi · fi auf Summe der Merkmalsträger ∑ fi. Dabei sind zwei Extreme möglich:
die Merkmalssumme ist gleich auf die Merkmalsträger verteilt. Konkret heißt das, dass die Gesamtheit der Vermögen gleich verteilt ist. Oder
die Merkmalssumme ist nur einem Merkmalsträger zugeteilt. Konkret heißt das, eine Person besitzt alles.
Graphisch lässt sich das Verhältnis von Merkmalssumme und Summe der Merkmalsträger in einem Koordinatensystem darstellen, bei dem die kumulierten %-Anteile der Merkmalssumme auf der Y-Achse, die kumulierten %-Anteile der Häufigkeiten auf der X-Ache aufgetragen werden (vgl. Abb. 6-1).
Gleichverteilung bedeutet, dass die ersten 10% der Betroffenen über 10% des Vermögens verfügen, die ersten 20% über 20% des Vermögens, usw. Dies wird über die 45°-Linie markiert.
Ungleichverteilung liegt vor, wenn z.B. die unteren 90% der Betroffenen über 10% des Vermögens und die oberen 10% über 90% verfügen. Dies lässt sich über den unteren Linienzug, die Lorenzkurve ausdrücken.
Abb. 6-1: Lorenz-Kurven bei Gleich- und Ungleichverteilung
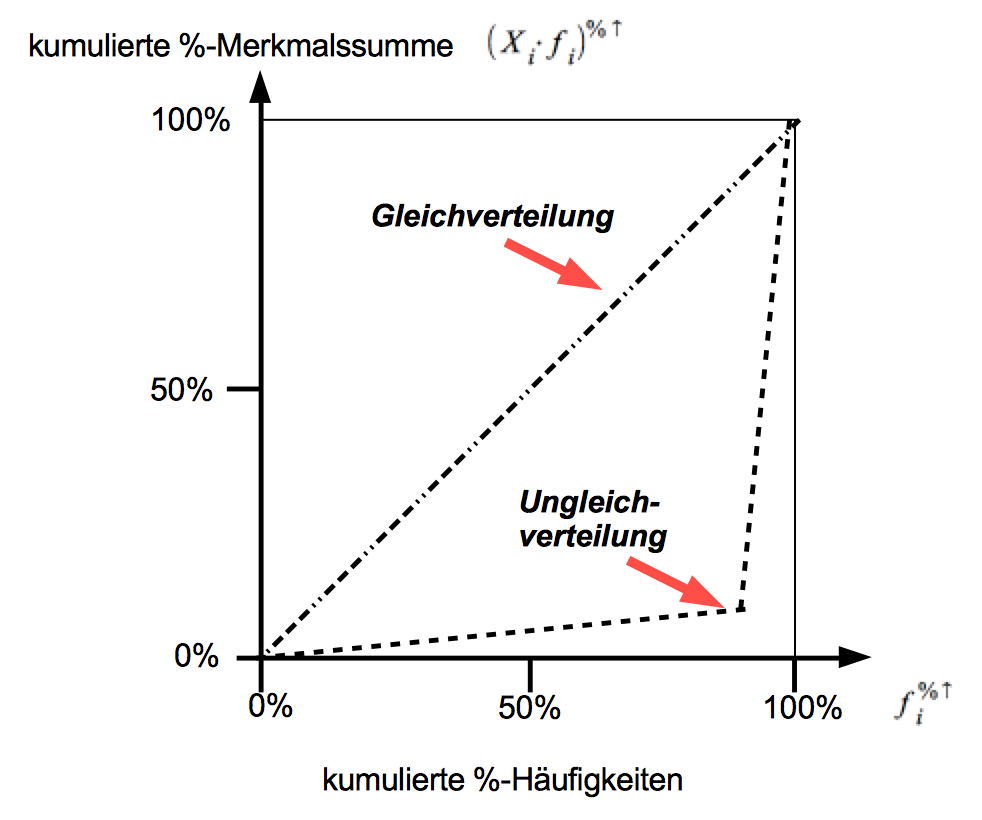
Das Ausmaß der realen Konzentration ergibt sich aus der Fläche zwischen der Gleichverteilungslinie und der Ungleichverteilungskurve. Die Konstruktion dieser Lorenzkurve soll an einem konkreten tabellarischen Beispiel demonstriert werden, wobei die Ordinatenpunkte der Kurve in der 7. Spalte der Tabelle und die Abszissenwerte in der 3. Spalte zu finden sind.
2. Die rechnerische Umsetzung
a) Das Fallbeispiel
Das Modell der relativen Konzentration soll im Folgenden am
Beispiel der studentischen Urlaubsausgaben aus Kap. 3 entwickelt
werden. Diese Verteilung wurden zur Vereinfachung in fünf
Klassen zusammengefasst. Anhand der Daten soll die Frage beantwortet
werden, in welchem Ausmaß sich die Urlaubsausgaben auf die
einzelnen Gruppen von Studierenden konzentriert.
b) Die Arbeitstabelle
Dazu müssen, wie in der folgenden Arbeitstabelle ausgewiesen,
die Häufigkeiten je Klasse (Spalte fi) und die Merkmalssummen je
Klasse (Spalte 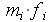 ) prozentuiert werden (Spalte
) prozentuiert werden (Spalte 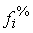 und
und 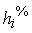 ). Dabei
wird
). Dabei
wird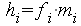 gesetzt.
Die Prozentwerte werden in Spalte
gesetzt.
Die Prozentwerte werden in Spalte 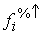 und
und 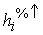 aufkumuliert.
aufkumuliert.
Tab.6-1: Arbeitstabelle zur Bestimmung der Lorenz-Kurve
und des Gini-Koeffizienten
|
|
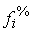
Sp 2 |
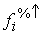
Sp 3 |
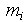
Sp 4
|
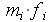
Sp 5
|
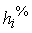
Sp 6 |
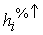
Sp 7 |
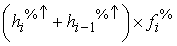
Sp 8
|
|
|
| 0 |
250 |
17 |
17.0000 |
17.0000 |
125.0000 |
2125.0000 |
3.0368 |
3.0368 |
51.6256 |
| 250 |
650 |
38 |
38.0000 |
55.0000 |
450.0000 |
17100.0000 |
24.4373 |
27.4741 |
1159.4141 |
| 650 |
850 |
22 |
22.0000 |
77.0000 |
750.0000 |
16500.0000 |
23.5798 |
51.0539 |
1727.6170 |
| 850 |
1150 |
14 |
14.0000 |
91.0000 |
1000.0000 |
14000.0000 |
20.0071 |
71.0611 |
1709.6106 |
| 1150 |
3350 |
9 |
9.0000 |
100.0000 |
2250.0000 |
20250.0000 |
28.9389 |
100.0000 |
1539.5498 |
| Summe |
100 |
100 |
- |
- |
- |
100 |
- |
6187.8171 |
Die Werte in den Spalten 2 und 6
besagen z.B. für die erste Zeile, dass die sparsamsten 17% der Studierenden nur über 3,04% der gesamten
Ausgabensumme verfügen und für die letzte Zeile, dass den
am aufwändigst reisenden 9% der Studierenden 28,9% der Ausgabensumme
zur Verfügung stehen.
3. Die Lorenz-Kurve
a) Das Konstruktionsprinzip
Zur Darstellung der Lorenz-Kurve werden die Werte der Spalten 3
und 7 in ein Koordinatensystem eingetragen. Dessen X-Achse weist die
kumulierten prozentualen Häufigkeiten (Spalte 3) und dessen
Y-Achse die kumulierten prozentualen Anteile an der Merkmalssumme
(Spalte 7) aus. Für die Zeichnung der Lorenzkurve können
auch die relativen kumulierten Häufigkeiten
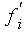 und
und
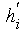 verwendet
werden.
verwendet
werden.
b) Die Darstellung der Lorenzkurve
Abb. 6-2: Lorenz-Kurve der Konzentration der Urlaubsausgaben
Oldenburger Studierender
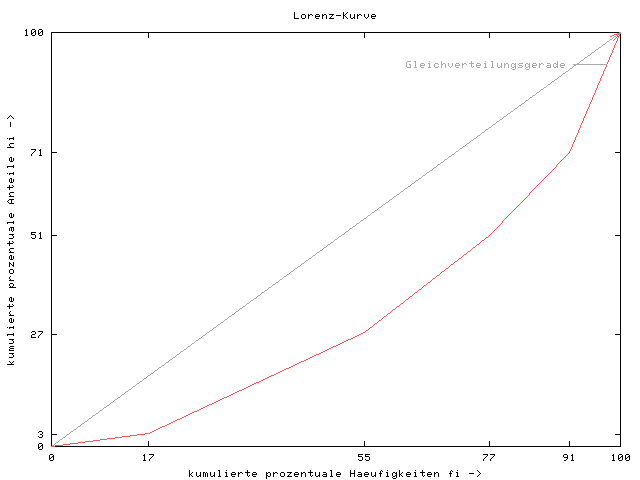
c) Die Aussage der Lorenzkurve
Das Ausmaß der Konzentration kann am Abweichen der
Lorenz-Kurve von der 45°-Linie gemessen werden. Da sich diese
45°-Linie bei völliger Gleichverteilung der Urlaubsausgaben
ergäbe, entsprächen sich jeweils der relative Anteil der
Häufigkeiten in den Ausgabenklassen und ihr Anteil an der
Merkmalssumme.
4. Der Gini-Koeffizient
a) Das Konstruktionsprinzip
Für die Berechnung des Gini-Koeffizienten benötigen wir
die letzte Spalte der obigen Arbeitstabelle, in der die Summe jeweils
zweier aufeinander folgender Werte mit den aufkumulierten
prozentualen Häufigkeiten multipliziert werden. Der
Gini-Koeffizient ergibt sich dann (Ableitung vgl. Litz, Statistische Methoden in den Wirtschafts- und Sozialwissenschaften, 3. Aufl. S. 111
ff.) über die Spaltensumme der Spalte 8 wie folgt:
b) Die Formel bei der Eingabe von %-Werten
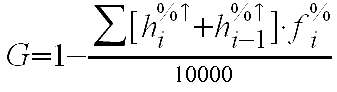
Es
gilt:
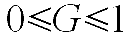
c) Die Formel bei der Eingabe von relativen Werten
Legt
man der Berechnung anstelle der Prozentwerte die relativen
Anteilswerte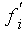 und
und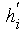 zugrunde
lautet die Formel:
zugrunde
lautet die Formel:
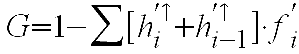
d) Die Interpretation des Ergebnisses
Für unsere
Urlaubsaufwendungen erhalten wir demnach einen Wert von:
G = 1 - 0.6188 =0.3812
Da G in einem linearen Verhältnis zur Stärke der
Konzentration steht, muss von einer eher geringen Konzentration
gesprochen werden. Generell können bei der Interpretation der
Gini-Koeffizienten folgende Aussagen gemacht werden:
0,0 < G < 0,2 : sehr schwache Konzentration
0,2 < G < 0,4 : schwache Konzentration
0,4 < G < 0,6 : mittlere Konzentration
0,6 < G < 0,8 : starke Konzentration
G
0,8 < G < 1,0 : sehr starke Konzentration.
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel06_Statistische~~lKonzentrationsma~~sze/modul01_Die~~lrelative~~lKonzentration/ebene01_Konzepte~~lund~~lDefi
nitionen/06__01__01__01.php3