 |
Beispiele und Aufgaben im Modul V-1 Schiefe, Fechnersche Lageregel und Schiefemaße
1. Beispiele
a) Zum Schiefemaß nach Pearson
Die Aussagen dieses Schiefemaßes sollen am praktischen
Beispiel der Wartezeiten aus unserer obigen Graphik demonstriert
werden. Dazu sind hier die in Kap. 3 berechneten Mittelwerte
aufgeführt:
-
|
arithmetisches Mittel:
|
|
10,5 Min.
|
|
Median:
|
|
11,0 Min.
|
|
Modus:
|
|
11,2 Min
|
Ihre Reihenfolge weist nach der Fechnerschen
Lageregel auf eine links-schiefe Verteilung hin.
Unter Verwendung der für diese Verteilung
ermittelte Standardabweichung von s = 3,60 ergibt sich einen
Pearsonsches Schiefemaß von:
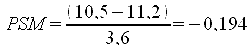
Dieser Wert drückt zahlenmäßig
eine leichte Linksschiefe aus.
b) Zur Berechnung der Schiefe mit SPSS
SPSS berechnet ein Schiefemaß auf der Basis von v .
Die Berechnung mit SPSS wird über die Befehlskette:
Analysieren > Deskriptive Statistiken > Häufigkeiten > Statistiken > Schiefe erzeugt.
Als Beispiel wurde die Schiefe für die Variablen partprof und partpot mit folgendem Ergebnis berechnet
Screenshot 5-1: Schiefemaß v mit SPSS
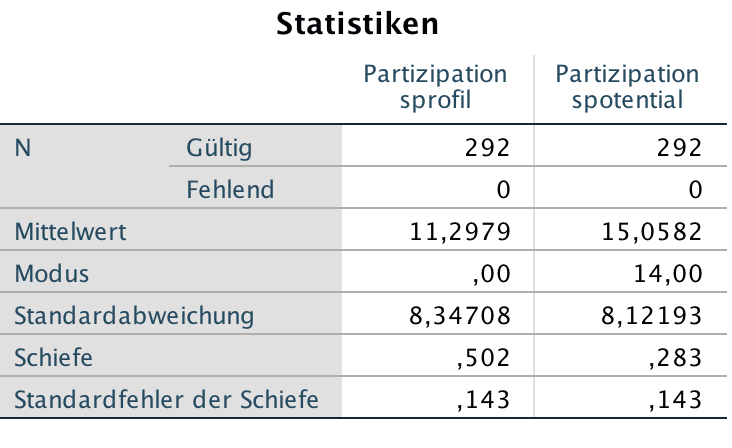
Interpretation der Ergebnisse und Vergleich mit den Schiefemaßen von Pearson
Das Schiefemaß v weist für die Variable partprof eine deutliche (v = 0,502), für die Variable partpot eine schwächere (v = 0,283) Schiefe auf.
Stellt man diesen Maßen die Berechnungen nach Pearson gegenüber, so ergibt sich
für partprof bei einem MOD = 0 ein PSM = 1,35. Da die Verteilung aber bimodal ist, empfiehlt es sich den zweiten Modalwert von "7" zu verwenden. Dies ergibt einen PSM-Wert von 0,51, der in etwa identisch mit dem v-Wert ist.
für partpot ergibt sich ein PSM-Wert von 0,131, der deutlich unter dem entsprechenden v-Wert liegt.
Letztlich können zur Beurteilung der Ergebnisse noch die entsprechenden Histogramme herangezogen werden.
2. Aufgaben
a) Die Ausgangsverteilung
Abb. 5-3: Verteilung der Urlaubsausgaben von
Studierenden
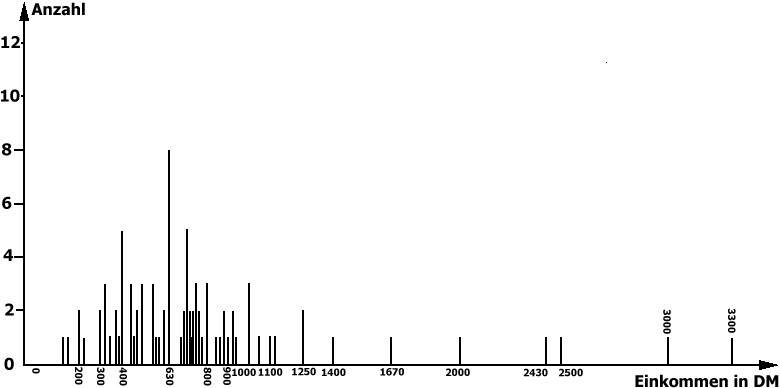
Wie beurteilen Sie die Schiefe anhand dieser Darstellung?
b) Die statistischen Maßzahlen
Für diese Grafik ergaben sich aus den
Originaldaten folgende statistischen Maßzahlen:
-
|
Anzahl der Fälle
|
88,00
|
|
arithmetisches Mittel
|
769,00
|
|
Modus
|
600,00
|
|
Median
|
685,00
|
|
Standardabweichung
|
553,17
|
c) Die Überprüfung der Ergebnisse
Bestimmen Sie mit Hilfe
der Fechnerschen Lageregeln und des PSM die Schiefe für die Verteilung
der monatlichen Urlaubsausgaben Oldenburger Studenten und tragen Sie Ihre Antworten in folgende multiple choice-Kontrolle ein:
|



