 |
Konzept und Definition im Modul III-3 Das arithmetische Mittel
1. Das Konzept des arithmetischen Mittels
Das arithmetische Mittel
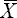(sprich "x quer") ist der im Alltag am häufigsten verwendete
Mittelwert. Es drückt aus, was im
Allgemeinen als rechnerischer Durchschnitt verstanden wird.
Bei seiner Berechnung werden alle Merkmalswerte aufsummiert. Die Summe wird dann durch die Anzahl der Beobachtungen dividiert. Praktisch hieße das, dass die Merkmalswerte (also z.B. die individuellen Fehlerpunkte in einer Statistikklausur oder die jeweils verfügbaren monatlichen Mittel) gleichmäßig auf die Betroffenen verteilt würden.
Damit eine Summierung Sinn macht, müssen die Merkmale metrisch skaliert sein.
Da in die Berechnung alle Beobachtungen eingehen, reagiert das arithmetische Mittel extrem auf Ausreisser.
Im konkreten Fall sollte deshalb geprüft werden, ob
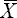ein angemessener Mittelwert ist, wenn es mehr auf die Lage des
Zentrums der Verteilung und weniger auf den Aspekt einer
gleichmäßigen Aufteilung der Merkmale auf die
Merkmalsträger ankommt.
2. Die formalen Definitionen
Die jeweils konkret anzuwendende Formel richtet sich nach der Art und Weise, in der die Daten aufbereitet wurden.
Die Formel-Übersicht
Abbildung 3-7: Formeln zur Berechnung des Mittelwertes
Die Formel für nicht gruppierte Daten
Die Formel für das arithmetische Mittel aus den Original-Daten summiert alle beobachteten Werte X i auf und dividiert
diese durch die Anzahl N der Beobachtungen.
Der Index i drückt dabei die lfd. Nummer der Beobachtung aus.
Die Formel für gruppierte Daten
Bei gruppierten Daten summiert man alle Produkte X i · f i auf und teilt diese durch N.
Der Index i drückt dabei die lfd. Nummer der
gruppierten Beobachtung aus.
Die Formel für klassierte Daten
Bei klassierten Daten werden alle Produkte m i · f i aufsummiert und durch N geteilt.
m i symbolisiert dem Mittelpunkt der Klassen, der Index i die lfd. Nummer der
Klasse aus.
Zu beachten ist, dass die Berechnung
aus nicht-klassierten Daten zu dem genauen Ergebnis führt, die aus
klassierten Daten nur zu einem annähernden Ergebnis.
|
