 |
Beispiele und Aufgaben im Modul II-5 Die graphische Darstellung klassierter Daten
1. Beispiele
a) Konstruktionsprinzipien und Fehlerquellen beim Histogramm
Wir greifen nochmals das Beispiel der Wartezeiten in einer Arztpraxis auf, die in der Tabelle 2-20 festgehalten waren:
Tabelle 2-20: Wartezeiten in einer
Sprechstunde
|
Wartezeit in Minuten
von... bis unter...
|
absolute Häufigkeit
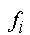
|
Klassen- breite
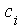 |
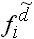
(mit 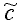 =2) =2)
|
|
1-5 |
1 |
4 |
0,5 |
|
5-10 |
2 |
5 |
0,8 |
|
10-12 |
4 |
2 |
4 |
|
12-14 |
2 |
2 |
2 |
|
14-20 |
1 |
6 |
0,3334 |
|
Summe: |
10 |
- |
- |
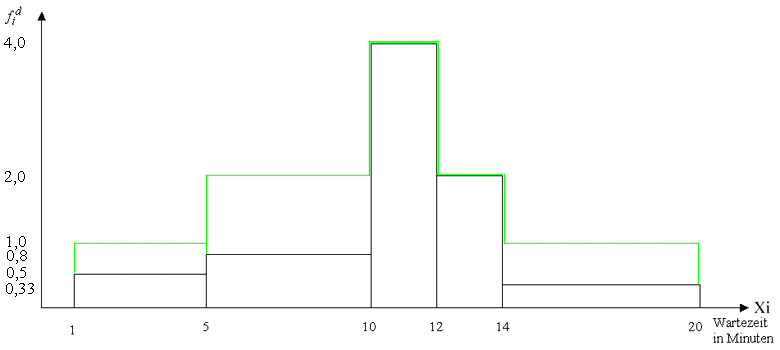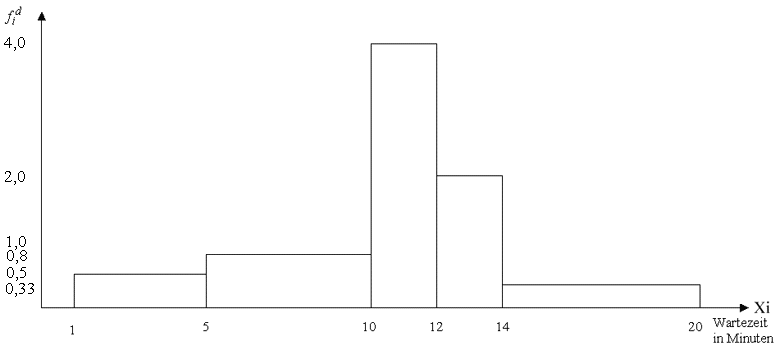
Zur Verdeutlichung der Verwendung der Häufigkeitsdichten wurde das Histogramm
auch mit den fehlerhaften, absoluten Häufigkeiten gezeichnet, hier . Man sieht, dass mit diesen Daten ein ganz
anderes Bild entsteht!
Abbildung 2-20: Histogramm der Wartezeiten in einer Sprechstunde
a) Konstruktionsprinzipien und Fehlerquellen beim Polygonzug
Die Konstruktion des Polygonzuges ergibt sich im Einzelnen unter
Beachtung folgender Regeln:
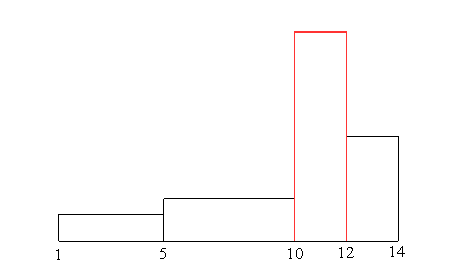
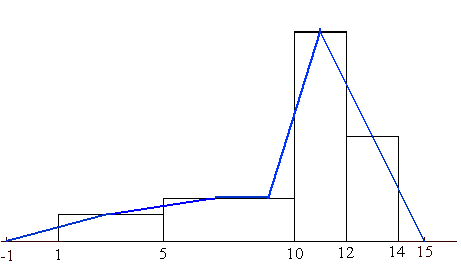
Abbildung 2-21: Konstruktionsgraphik zum Polygonzug
1. |
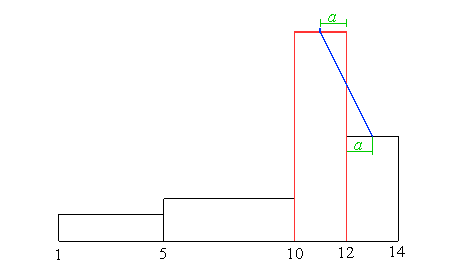
Angesetzt wird der Polygonzug immer am schmalsten Balken. Gibt es
mehrere, ist die Reihenfolge beliebig. Hier wird mit dem Balken der Klasse
10-12 angefangen, der rot gekennzeichnet ist. |
|
2. |
Am schmalsten Balken wird nun die Mitte gesucht, hier blau dargestellt.
Die Entfernung von der Mitte bis zum Klassenrand bezeichnen wir als
a, hier grün. |
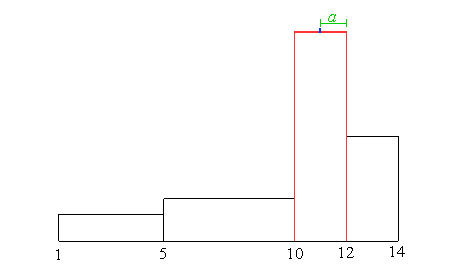
|
3. |
Jetzt wird eine Linie zum nächsten Balken gezogen. Der Endpunkt ist in
Betrag a von der Klassengrenze entfernt. |
|
4. |
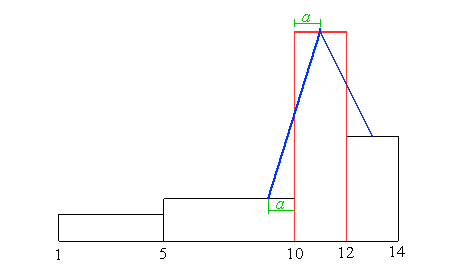
Das gleiche geschieht nun auf der anderen Seite. Der Abstand a bleibt
dabei gleich groß.
Damit ist der Polygonzug für die Klasse 10-12 und
teilweise für die Nachbarklassen fertig. |
|
5. |
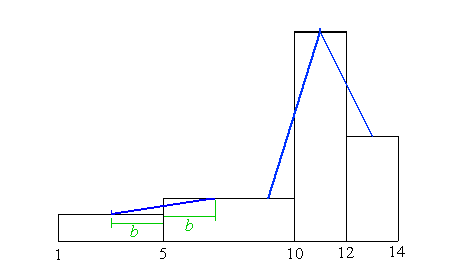
Bei den Klassen 1-5 und 5-10 ist die erstere die schmalere, also wird
mit ihr begonnen.
Wieder wird die Klassenmitte gesucht und der Abstand
- nennen wir ihn nun b - auf dem Nachbarbalken abgetragen.
Dann
kann auch hier die Linie gezogen werden. |
|
6. |
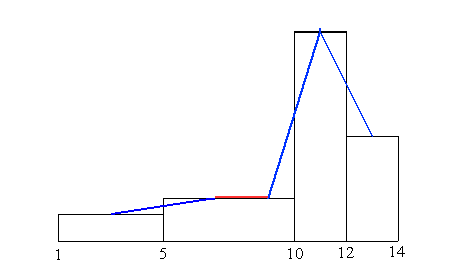
Im nächsten Schritt werden die beiden Linienendpunkte auf der Oberkante
der Klasse 5-10 miteinander verbunden, hier rot dargestellt. |
|
7. |
Zu letzt muss das Histogramm noch geschlossen werden werden. (Zur
Erinnerung: Das Histogramm ist eine flächenproportionale Darstellung!)
Dazu konstruieren wir zwei neue Klassen, eine für den Anfang, die andere
für das Ende. Beide Klassen sind halb so groß wie die folgende, bzw. die
vorhergehende. So entsteht eine Klasse von -1 bis 1 und eine Klasse von 14
bis 15. Der Polygonzug wird nun auf die X-Achse gezogen, so dass er auf
den Anfang der ersten, bzw. das Ende der letzten Klassen trifft. Das
Histogramm ist damit fertig. |
|
Aufgaben zur Konstruktion von Histogrammen und Polygonzügen finden Sie im nächste Arbeitsschritt.
|



