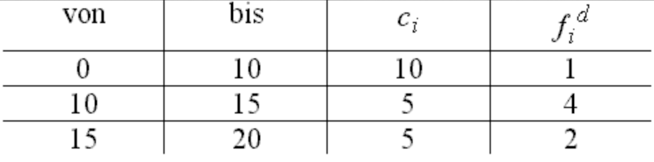
Tabelle 2-19: ungleiche Klassenbreiten und Häufigkeitsdichten
xu ...... xo
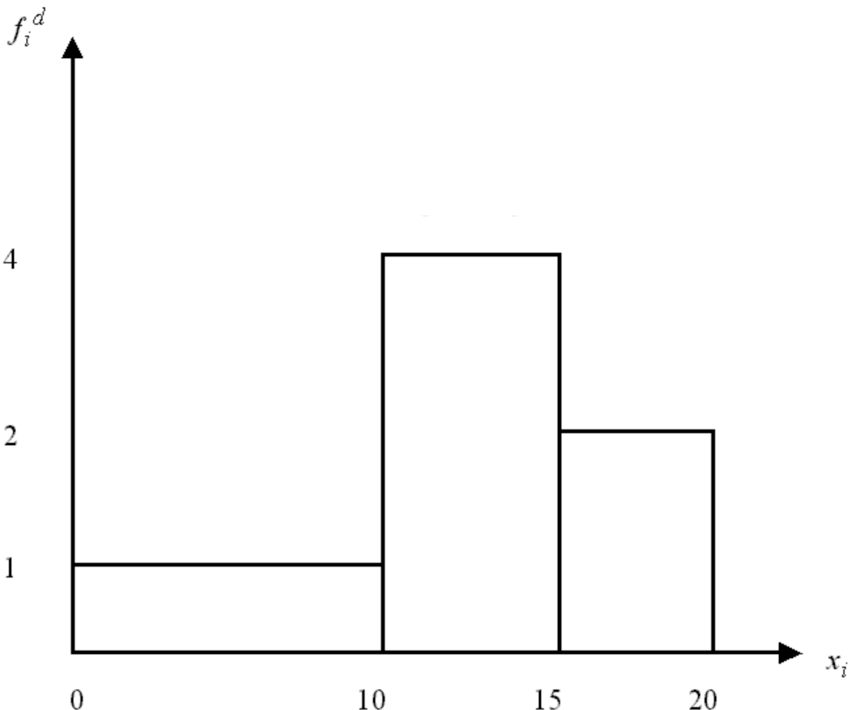
Das Histogramm wird in ein Koordinatensystem eingezeichnet, wobei auf der
X-Achse das beobachtete Merkmal 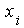 (bzw. die
Klassengrenzen
(bzw. die
Klassengrenzen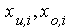 ) und auf der Y-Achse die (modifizierten)
Häufigkeitsdichten abgetragen werden. In seiner Breite ist der Balken also durch
Klassenunter- und -obergrenze determiniert, die Höhe drückt sich durch die
Häufigkeitsdichte aus.
) und auf der Y-Achse die (modifizierten)
Häufigkeitsdichten abgetragen werden. In seiner Breite ist der Balken also durch
Klassenunter- und -obergrenze determiniert, die Höhe drückt sich durch die
Häufigkeitsdichte aus.
Abbildung 2-16 Histogramm bei ungleichen Klassenbreiten
Simulation
|

|
Diese Simulation zeigt alle Schritte für das Zeichnen eines Histogramms
|
b) Eine konkrete Anwendung
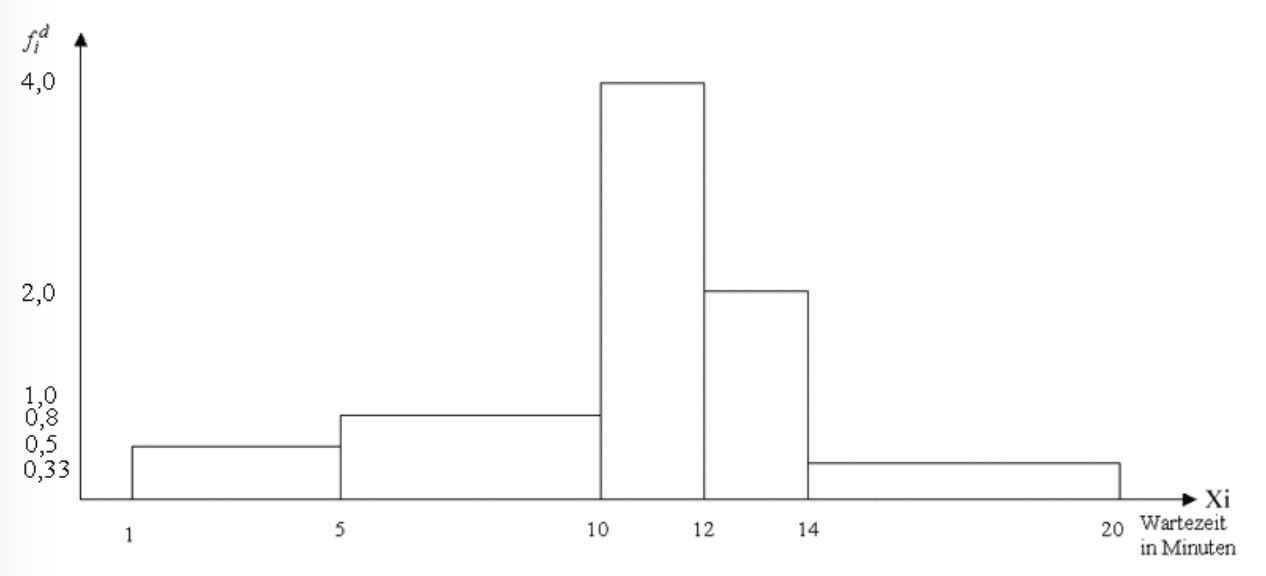
Dabei wird ein bereits in Kap. II-3 angesprochenes Beispiel zur Wartezeit in einer Arztpraxis zugrunde gelegt. Das Ergebnis ist in der folgenden klassierten Tabelle festgehalten:
Tabelle 2-20: Wartezeiten in einer
Sprechstunde
|
Wartezeit in Minuten
von... bis unter...
|
absolute Häufigkeit
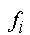
|
Klassen- breite
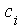 |
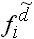
(mit 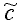 =2) =2)
|
|
1-5 |
1 |
4 |
0,5 |
|
5-10 |
2 |
5 |
0,8 |
|
10-12 |
4 |
2 |
4 |
|
12-14 |
2 |
2 |
2 |
|
14-20 |
1 |
6 |
0,3334 |
|
Summe: |
10 |
- |
- |
Aus dieser Tabelle ergibt sich das Histogramm wie folgt:
Abbildung 2-17: Histogramm der Wartezeiten in einer
Sprechstunde
3. Die Konstruktion des Polygonzuges bei unterschiedlichen Klassenbreiten
Der Polygonzug stellt eine
Modifikation und Glättung des Histogramms dar. Diese gibt die bisher im
Histogramm implizit enthaltene Annahme der Gleichverteilung der Beobachtungen
innerhalb der Klassengrenzen auf. Dem Polygonzug liegt dagegen die Vermutung
zugrunde, dass sich die Werte im Histogramm eher in den Klassenhälften häufen,
die an eine insgesamt stärker besetzte Klasse angrenzen. Man erhält so eine
angemessenere Darstellung der vermuteten Verteilungsform.
a) Das Konstruktionsprinzip
Die nachfolgende Konstruktion bezieht sich auf die in 2.a) präsentierte Tabelle 2-19.
Zu beachten ist, dass die Fläche unter dem Polygonzug (in der Grafik blau gezeichnet) der Fläche des Histogramms entsprechen muss. Dieses wird erreicht, wenn die von der rechteckigen Fläche abgetrennten Dreiecke den Nachbarklassen zugeteilt werden.
Abbildung 2-18: Polygonzug bei ungleichen Klassenbreiten
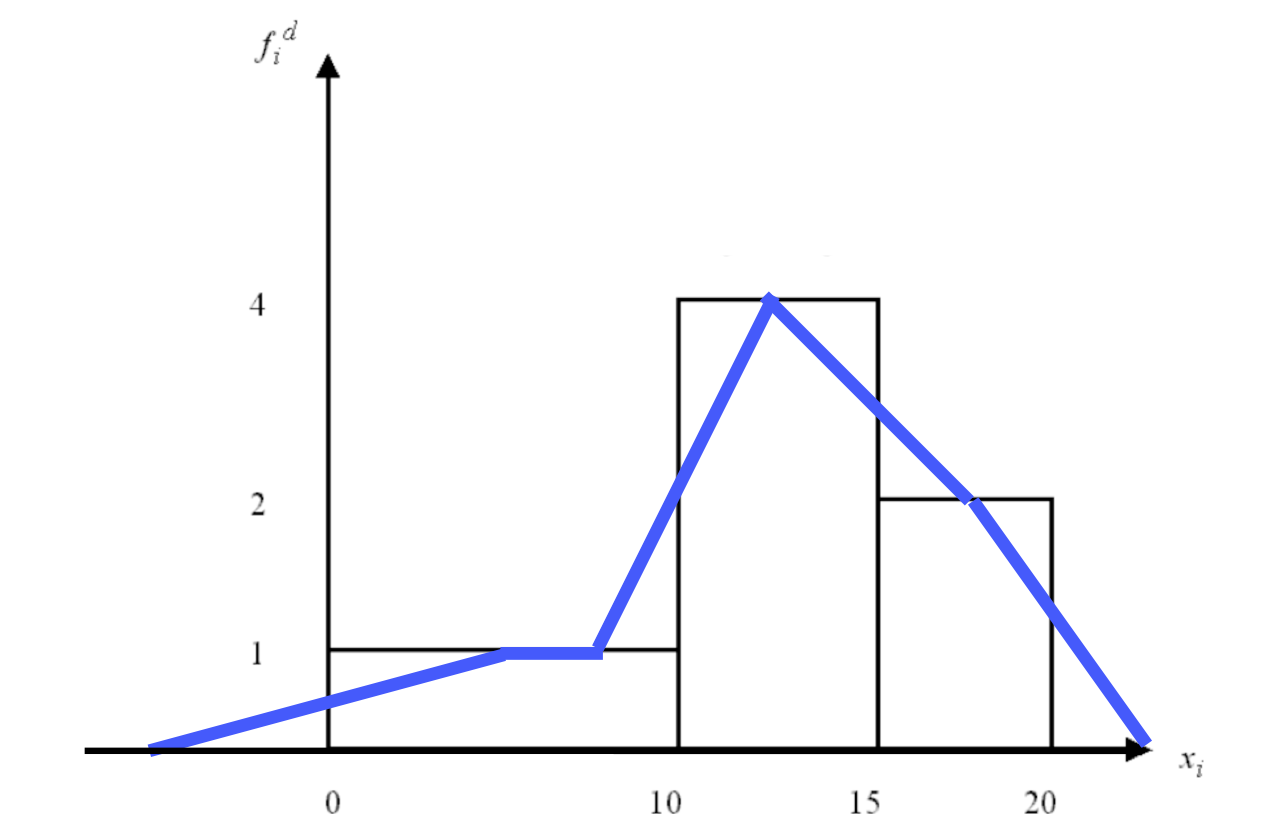
Ausgangspunkt der Konstruktion ist die Klassenmitte des Rechtecks mit der geringsten Klassenbreite. Von dort werden die Linien zu den Nachbarklassen so gezogen, dass diese im Abstand der halben Klassenbreite der Ausgangsklasse an den Oberkanten der Nachbarklassen enden. Dieses Konstruktionsprinzip wird in der nachfolgenden Animation verdeutlicht.
b) Eine Animation zum Konstruktionsprinzip
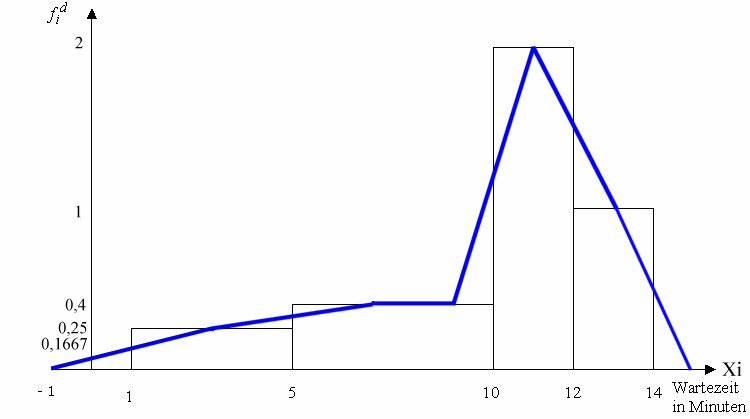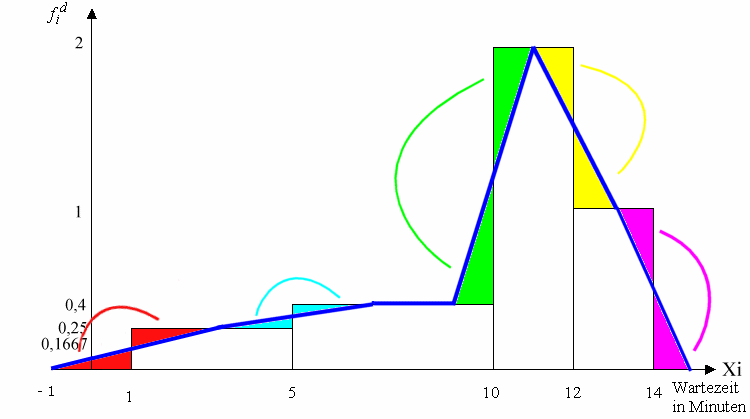
In der Graphik wird die Entsprechung der Flächen vom Histogramm und unter dem Polygonzug durch die
Gleichfarbigkeit der verlagerten Dreiecke gezeigt.
Abbildung 2.19: Polygonzug zu den Wartezeiten in einer Arztpraxis
Die einzelnen Schritte der Konstruktion werden im nachfolgenden Abschnitt im Detail vorgestellt.



