Konzepte und Definitionen im Modul II-2 Die tabellarische Darstellung eindimensionaler Häufigkeiten
1. Die Grundauszählung
a) Die Ordnung der Daten
In der Urliste sind die Informationen meist nicht geordnet und es sind keine
Zusammenfassungen in Gruppen oder Klassen vorhanden. Der erste Schritt
der Aufbereitung besteht deshalb in der Ordnung der Einzelangaben
je Merkmal nach bestimmten Ordnungsprinzipien:
Bei quantitativen Merkmalen
orientiert man sich dabei an der Höhe der Merkmalswerte,
bei qualitativen
Merkmalen an fachsystematischen Aspekten und
bei alpha-numerischen Informationen ergibt sich eine Ordnung nach dem Alphabet.
Die auf diese Weise erhaltene Tabelle wird als Primärtabelle bezeichnet.
Die Kopfzeile der Tabelle enthält das Merkmal Xi. Zu beachten ist dabei, dass die einzelnen Merkmalsausprägungen über die Anzahl N der Objekte laufen, d.h. i = 1....N.
b) Die Gruppierung der Daten
Durch die Gruppierung
von Daten der Primärtabelle in eine geordnete Liste können die Informationen knapper und übersichtlicher
gestaltet werden. Bei diesem Vorgang werden alle Merkmalsträger, welche das
gleiche Merkmal aufweisen, zusammengefasst. Dabei tritt kein Informationsverlust
auf.
Den so entstandenen Merkmalsausprägungen Xi sind die
Häufigkeit fi mit i = (1....k) zugeordnet, d.h. diesmal läuft der Index i über die Anzahl k der unterschiedlichen Merkmalsausprägungen.
Das Symbol fi leitet sich aus dem Englischen (frequencies)
ab.
2. Die eindimensionale Häufigkeitsverteilung
Das Ergebnis der Gruppierung ist eine einfache (nicht klassierte)
Häufigkeitsverteilung des Merkmals Xi.
a) Absolute, relative und prozentuale Häufigkeiten
In den meisten Fällen liegen die Häufigkeiten fi in absoluten Werten vor.
Für viele Fragestellungen,
vor allem für Vergleiche von unterschiedlich großen Mengen gleicher Objekte ist
auch die Verwendung von relativen 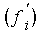 oder
prozentualen oder
prozentualen 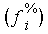 Häufigkeiten sinnvoll. Häufigkeiten sinnvoll.
Ausgehend
von absoluten Werten können relative und prozentuale Häufigkeiten sehr einfach
berechnet werden:
b) Die eindimensionale Häufigkeitstabelle
Die unter a) angeführten Häufigkeiten lassen sich einfach in tabellarischer Form mittels einer einfachen
Häufigkeitstabelle darstellen. Hier demonstriert an absoluten Werten:
Tabelle 2-1: Allgemeine Form einer einfachen
Häufigkeitstabelle

In der Kopfzeile sind das Merkmal Xi und die
Häufigkeit fi ausgewiesen.
In der Vorspalte sind die einzelnen unterschiedlichen Ausprägungen des Merkmals Xi angeführt.
In der zweiten Spalte, dem Tabellenkern, finden sich die Häufigkeiten fi mit i = (1....k) .
In der letzten Zeile, der Summenzeile, ergibt sich mit N die Anzahl der erfassten Elemente, da gilt ∑ fi = N.
3. Die kumulierte Häufigkeitstabelle
Das Auf- und Abkumulieren (auch Kumulieren und Dissipieren) von Häufigkeiten
stellt eine weiter Form der Aufbereitung statistischer Daten dar. Dabei werden
aufeinander folgende Merkmalsausprägungen zusammengefasst. Die Kumulation setzt
also mindestens ordinal-skalierte Daten voraus.
a) Das Konzept der Aufwärts-Kumulation
Beginnt man am unteren Ende der Tabelle und fasst zunehmend höher
Merkmalswerte zusammen spricht man von Auf(wärts-)kumulation. Die
Merkmalsausprägungen ergeben sich dabei in der Form: "bis-unter" (oder
auch als "weniger als")
Die Merkmalsausprägungen
erscheinen bei der Aufwärtskumulation in der Form "bis unter 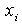 " oder "mehr
als " oder "mehr
als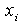 " . Die Häufigkeiten " . Die Häufigkeiten 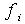 werden entsprechend aufaddiert. werden entsprechend aufaddiert.
Dies sei an der folgenden allgemeinen
Häufigkeitstabelle demonstriert. Dabei werden absolute Häufigkeiten zugrunde
gelegt. Das Verfahren gilt aber analog für relative und prozentuale
Häufigkeiten:
Tabelle 2-2: Ausgangstabelle für die
Kumulation:
|
Merkmalsausprägung
von... bis unter...
|
absolute Häufigkeit
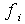 |
|
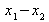
|
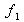
|
|
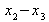
|
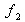
|
|
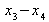
|
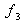
|
|
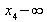
|
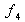
|
|
Summe: |
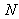
|
In der folgenden Tabelle wird das Verfahren
verdeutlicht. Es ergeben sich die aufkumulierten absoluten Häufigkeiten oder
Summenhäufigkeiten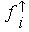 . .
Tabelle 2-3: Auf(wärts-)kumulation von
Merkmalshäufigkeiten
|
Merkmalsausprägung
bis unter ... |
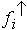
|
|
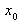
|
0 |
|
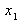
|
f1 |
|
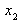
|
f1 + f2 |
|
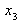
|
f1 + f2 + f3
|
|
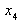
|
f1 + f2 + f3 +
f4 = N |
b) Das Konzept der Abwärts-Kumulation
Beginnt man mit der Zusammenfassung der
Merkmalswerte am oberen Ende der Tabelle, also bei 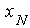 oder bei oder bei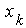 , spricht man von einer
Ab(wärts-)kumulation. Man erhält dann die Merkmalsausprägungen �bis unter , spricht man von einer
Ab(wärts-)kumulation. Man erhält dann die Merkmalsausprägungen �bis unter
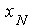 oder oder 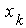 �
und die dazu gehörenden abkumulierten Häufigkeiten �
und die dazu gehörenden abkumulierten Häufigkeiten 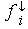 .
Auf der Basis der obigen Ausgangstabelle ergibt sich die folgende Tabelle der
abkumulierten Häufigkeiten: .
Auf der Basis der obigen Ausgangstabelle ergibt sich die folgende Tabelle der
abkumulierten Häufigkeiten:
Tabelle 2-4: Ab(wärts-)kumulation von
Merkmalshäufigkeiten
|
Merkmalsausprägung
... und mehr |
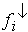
|
|
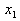
|
N |
|
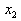
|
N - f1 |
|
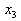
|
N - f1 - f2 |
|
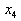
|
N - f1 - f2 - f3
|
|

|
N - f1 - f2 - f3 -
f4 =0 |
| 


