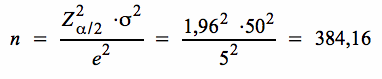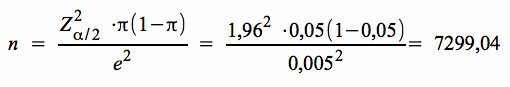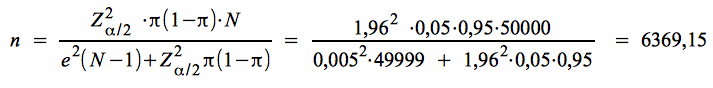Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

1. Beispiele und Aufgaben zur Bestimmung des Stichprobenumfangs bei einer Schätzung des Mittelwerts μ

a) Beispiel zur Bestimmung des Stichprobenumfangs

In Aufgabe 47 hatte eine Supermarktkette mit einem Konfidenzniveau von 0,95 eine Schätzung der Ausgaben der Haushalte für Lebensmittel vorgenommen und dazu eine Stichprobe im Umfang von n = 100 durchgeführt. Dabei ergab sich ein ŝ von 50 EUR und eine Spannweite für das Konfidenzintervall von etwa 20 EUR. Wie groß sollte der Stichprobenumfang sein, wenn der Schätzfehler 5 EUR nicht übersteigen soll.

Die Vorgaben

Eine Konfidenzschätzung für Haushaltsausgaben soll mit maximal einem e = 5 durchgeführt werden. Das Konfidenzniveau ist gegeben mit: 1- α = 0,95. Da σ unbekannt ist, arbeiten wir mit ŝ = 50, aus der Vorläuferstichprobe.

Prüfung der Voraussetzungen

Da n > 30 sein wird, können wir uns trotz unbekanntem σ bei der Schätzung auf die Normalverteilung von X̄ stützen.
Ein Endlichkeitsfaktor muss nicht bedacht werden.

Die Ermittlung des Z_α/2-Werts

Zur Durchführung der Schätzung benötigen wir den Z-Wert (Z_α/2), der sich für das gewählte Konfidenzniveau 1 - α = 0,05 ergibt. Aus der Tabelle erhalten wir: Z_α/2 = Z_0,975 = 1,96. Die dem vorgegebenen Signifikanzniveau entsprechenden z-Werte finden Sie in der Tabellenübersicht .

Durchführung der Berechnung

Aus der Formel für n erhalten wir folgenden Stichprobenumfang:



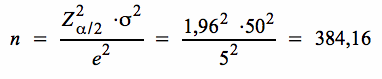
• Das Ergebnis der Berechnung

  Damit der Mittelwert der Grundgesamtheit µ mit einem Vertrauen von 95% auf 5 EUR genau geschätzt werden kann, ist ein Stichprobenumfang von 385 Haushalten notwendig.

b) Aufgaben zur Bestimmung des Stichprobenumfangs

Aufgabe 52

Die Partei A (vgl. das entsprechende Beispiel im Modul "Das allgemeine Schätzmodell) möchte wissen, wie es um ihre Glaubwürdigkeit in Fragen der inneren Sicherheit auf einer Skala von 0 - 10 bestellt ist. Wie groß muss die St Pr mindestens sein, wenn das Ergebnis mit einer Genauigkeit von 0,2 Punkten und einem Konfidenzniveau von 0,95 bestimmt werden soll. In einer früheren St Pr zum Thema streuten die Ergebnisse mit ŝ = 1,2 Punkten.
Diese Aufgabe ist hier in 5 Schritten zu lösen! Bitte geben Sie die Z-Werte in die Eingabefenster wie angegeben und die Resultate mit 2 Dezimal-Stellen ein. Die dem vorgegebenen Signifikanzniveau entsprechenden Z-Werte finden Sie in der Tabellenübersicht .

Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen zu berücksichtigen.

2. Beispiele und Aufgaben zur Bestimmung des Stichprobenumfangs bei einer Schätzung des Anteilswerts π

a) Beispiel zur Bestimmung des Stichprobenumfangs

Beispiel 1 ohne Berücksichtigung des Endlichkeitsfaktors

In Aufgabe 49 wurden die Chancen geprüft, ob eine Partei A die 5% Hürde überwinden könne. Das Konfidenzintervall betrug mehr als 1,7 %. Wie groß müsste eine Stichprobe sein, damit das vermuteten Ergebnis von A mit 95%iger Konfidenz auf 0,5% genau vorhergesagt werden kann? Die Größe des Wahlkreises soll vorerst keine Rolle spielen.

Die Vorgaben

Eine Konfidenzschätzung für Stimmanteile soll mit einem maximalen e = 0,005 durchgeführt werden. Das Konfidenzniveau ist gegeben mit: 1 - α = 0,95.

Prüfung der Voraussetzungen

π(1 - π) soll über ein p =0,05 (5%-Klausel) geschätzt werden
Ein Endlichkeitsfaktor muss vorerst nicht bedacht werden.

Die Ermittlung des Z_α/2-Werts

Zur Durchführung der Schätzung benötigen wir den Z-Wert (Z_α/2), der sich für das gewählte Konfidenzniveau 1 - α = 0,95 ergibt. Aus der Tabelle erhalten wir: Z_α/2 = Z_0,975 = 1,96. Die dem vorgegebenen Signifikanzniveau entsprechenden z-Werte finden Sie in der Tabellenübersicht .

Durchführung der Berechnung

Aus der Formel für n erhalten wir folgenden Stichprobenumfang:



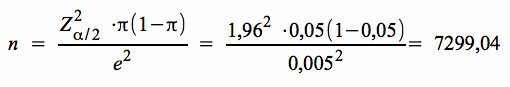
• Das Ergebnis der Berechnung

  Damit der Anteilswert der Grundgesamtheit π mit einem Vertrauen von 95% auf 0,5 % (d.h. auf eine Spanne von 4,5 - 5,5 %) genau geschätzt werden kann, ist ein Stichprobenumfang von mindestens n = 7300 Personen notwendig.

• Kommentar zum Ergebnis

  Betrachtet man die üblichen StPr-Umfänge bei Wahlprognosen, die etwa bei 1000 Befragten liegen, sind deren Aussagen nicht als sehr genau einzuschätzen.

Beispiel 2 mit Berücksichtigung des Endlichkeitsfaktors

In Aufgabe 49 sollte die Wahlprognose zu einer Gemeinderatswahl mit etwa 50 Tsd. Wahlberechtigten durchgeführt werden. Bei dem in Beispiel 1 errechneten St Pr Umfang von 7300 Befragten ist n/N > 0,05 also sollte der Endlichkeitsfaktor berücksichtigt werden. Wie groß müsste nun die Stichprobe sein, damit das vermuteten Ergebnis von A mit 95%-iger Konfidenz auf 0,5% genau vorhergesagt werden kann?

Die Vorgaben

Eine Konfidenzschätzung für Stimmanteile soll mit einem maximalen e = 0,005 durchgeführt werden. Das Konfidenzniveau ist gegeben mit: 1 - α = 0,95.

Prüfung der Voraussetzungen

π(1 - π) soll über ein p =0,05 (5%-Klausel) geschätzt werden
Ein Endlichkeitsfaktor muss bedacht werden.

Die Ermittlung des Z_α/2-Werts

Der Z-Wert (Z_α/2) ergibt sich für das gewählte Konfidenzniveau 1 - α = 0,95 wieder mit: Z_α/2 = Z_0,975 = 1,96.

Durchführung der Berechnung

Aus der Formel für n erhalten wir folgenden Stichprobenumfang:



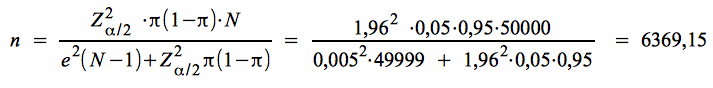
• Das Ergebnis der Berechnung

  Damit der Anteilswert der Grundgesamtheit π mit einem Vertrauen von 95% auf 0,5 % genau geschätzt werden kann, ist bei Berücksichtigung des Endlichkeitsfaktors ein Stichprobenumfang von mindestens n = 6370 Personen notwendig.

• Kommentar zum Ergebnis

  Auch wenn die Beachtung des EF zu einer Reduktion des StPr-Umfangs um fast 1000 Personen geführt hat, wird der Aufwand der Partei anlässlich einer Gemeindewahl zu hoch sein. Sie hat nur die Wahl entweder einen höheren Schätzfehler oder ein niedrigeres Konfidenzniveau in Kauf zu nehmen.

b) Aufgaben zur Bestimmung des Stichprobenumfangs

Aufgabe 53

Bei der Schätzung des Anteilswertes wurde als Beispiel die Ermittlung des Anteils von Haushalten im ländlichen Raum vorgestellt, die noch über keinen Netzzugang verfügen. Bei n = 100 erbrachte die Schätzung mit 1 - α = 0,99 eine Spanne von etwa 25 %. Wie groß müsste die StPr sein, wenn der Anteil mit gleichem Konfidenzniveau auf 5 % genau ermittelt werden soll?
Diese Aufgabe ist hier in fünf Schritten zu lösen! Bitte geben Sie die Z-Werte in die Eingabefenster wie angegeben und die Resultate mit 2 Dezimal-Stellen ein. Die dem vorgegebenen Signifikanzniveau entsprechenden Z-Werte finden Sie in der Tabellenübersicht . Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen zu berücksichtigen.

letzte Änderung am 5.4.2019 um 4:24 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel05/modul05/ebene02/05__05__02__01.php3