 |
Konzepte und Definitionen im Modul V-5 Bestimmung des Stichprobenumfangs n
Vorbemerkung
Wie in den vorangegangenen Modulen für die Schätzungen von μ und π festgestellt, halbiert eine Vervierfachung des Stichprobenumfangs die Spannweite des Konfidenzintervalls für μ bzw. π.
Man definiert als Schätzfehler e die halbe Spannweite des Konfidenzintervalls. Der maximal zulässige Schätzfehler e ist dann die maximal tolerierte Differenz zwischen dem jeweiligen Parameter der GG und dem der Stichprobe. Bei den Schätzungen von μ und π lässt sich der maximale Schätzfehlers e vorgeben und daraus die optimale Stichprobengröße ermitteln. U. U. ist dabei der Endlichkeitsfaktor EF zu berücksichtigen.
1. Die optimale Stichprobengröße für Mittelwert-Schätzungen
a) Das Konzept des Schätzfehlers bei Schätzungen von μ
b) Die Ermittlung von n ohne Berücksichtigung des Endlichkeitsfaktors
Aus
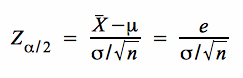 folgt durch Auflösung nach n: folgt durch Auflösung nach n:
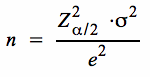
Da i. A. σ unbekannt ist, muss es vor der Ziehung der Stichprobe über eine Punkthypothese festgelegt werden. Erweist es sich nach der Ziehung, dass ŝ deutlich über dem hypothetischen σ-Wert liegt, sollte der Umfang der St Pr entsprechend vergrößert werden.
Unter Vorgabe des gewünschten Konfidenzniveaus lässt sich jetzt der optimale Stichprobenumfang für die Schätzung von μ berechnen.
c) Die Ermittlung von n mit Berücksichtigung des Endlichkeitsfaktors
Ist zu erwarten, dass n/N > 0,05, empfiehlt es sich, den Endlichkeitsfaktor 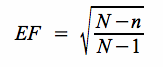 zu beachten. zu beachten.
Seine Berücksichtigung verkompliziert die Berechnung von n deutlich. Da EF < 1, führt dies zu einer Reduktion des Stichprobenumfangs, so dass der Aufwand in der Regel gerechtfertigt ist.
Aus
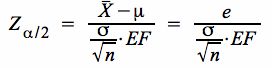 folgt durch Auflösung nach n: folgt durch Auflösung nach n:
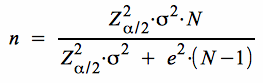
2. Die optimale Stichprobengröße für die Schätzung von Anteilswerten
a) Das Konzept des Schätzfehlers bei Schätzungen von π
Für Schätzungen von π ist der Schätzfehler e mit e = 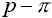 gegeben. gegeben.
b) Die Ermittlung von n ohne Berücksichtigung des Endlichkeitsfaktors
Aus
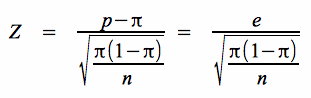
folgt durch Auflösung nach n:
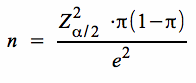
π · (1 - π) ist unbekannt und soll erst noch geschätzt werden. Manchmal ist es möglich, eine Abschätzung eines maximal zu erwartenden Anteils (etwa bezüglich eines Stimmenanteils einer Partei) vorzunehmen. Dann kann man mit dieser Schätzung arbeiten.
Wenn das nicht der Fall ist, ersetzt man π · (1 - π) durch sein insgesamt mögliches Maximum, das mit 0,52 gegeben ist und erhält:
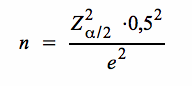
Unter Vorgabe des gewünschten Konfidenzniveaus lässt sich jetzt der optimale Stichprobenumfang für die Schätzung von π berechnen.
c) Die Ermittlung von n mit Berücksichtigung des Endlichkeitsfaktors
Auch bei der Schätzung von π empfiehlt es sich, den Endlichkeitsfaktor 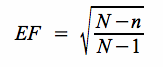 zu beachten, wenn zu erwarten ist, dass n/N > 0,05. zu beachten, wenn zu erwarten ist, dass n/N > 0,05.
Aus
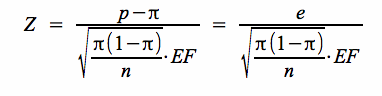
folgt durch Auflösung nach n:
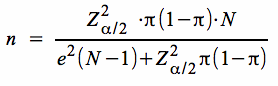
Da π · (1 - π) unbekannt ist, muss der Ausdruck entweder über den maximal zu erwartenden Anteil πmax oder durch das insgesamt mögliches Maximum von π · (1 - π) = 0,52 geschätzt werden.
|



