 |
Konzepte und Definitionen im Modul V-1 Allgemeine Aspekte des Schätzmodells (Punkt- und Intervallschätzungen)
Vorbemerkung
Der Hypothesentest hatte die Aufgabe auf Grund von Stichprobendaten über die Gültigkeit der Hypothesen H0 und H1 zu entscheiden. Die Konfidenzschätzung geht davon aus, dass es keine Kenntnisse über die Grundgesamtheit (GG) gibt und die notwendigen Parameter aus den Daten einer gezogenen Stichprobe geschätzt werden müssen.
Der Begriff des "Schätzens" birgt in sich die Gefahr, dass die Schätzung falsch ist, weil die Stichprobe die Grundgesamtheit nicht genau widerspiegelt. In diesem Fall liegt ein sog. Stichproben-Fehler vor. Dies führt dann zu "falschen" Schätzungen.
Im Folgenden betrachten wir die Konzepte, mit denen von einer Stichprobe auf die Parameter der Grundgesamtheit (μ, σ oder π) geschlossen werden kann. Ausgangspunkt sind dabei meist die entsprechenden Stichprobenstatistiken (X̄, ŝ und p). Dabei unterscheiden wir in Punkt- und Intervallschätzungen.
Bei einer Punktschätzung wird von den Stichprobenstatistiken unmittelbar auf den entsprechenden Parameter der Grundgesamtheit geschlossen. D. h. man arbeitet mit der Annahme, dass der Parameter der Grundgesamtheit der Stichprobenstatistik entspricht. Damit hat man zwar eine punktgenaue Aussage, trifft diese aber mit einem hohen Risiko.
Die Intervallschätzung räumt bereits von vorne herein einen gewissen Stichprobenfehler ein und sucht nach einem Konfidenzintervall (Vertrauensbereich), in dem der Parameter liegt. Dieser Bereich soll wenn möglich symmetrisch um die, aus der Stichprobe ermittelte Statistik konstruiert werden.
Zur Festlegung der Größe des Schätzbereichs muss zunächst das Konfidenz- oder Vertrauensniveaus 1 - α definiert werden. Für eine Schätzung gilt: Mit steigendem Vertrauensniveau wird die Aussage sicherer, aber auch unschärfer.
1. Die Punktschätzung
a) Die Ausgangslage
Die Punktschätzung ist ein Verfahren, das sich unmittelbar auf eine Stichprobenstatistik bezieht und deren Wert als Schätzung für den Parameter der Grundgesamtheit verwendet. Auf der Basis dieses Ansatzes wurde bereits beim Mittelwert-Test statt des unbekannten σ die Standardabweichung ŝ verwendet.
Die jeweils einer Schätzung konkret zugrunde gelegte Stichprobenstatistik T wird als
Schätzfunktion: T = f(Xi) , i = 1....n
der einzelnen Stichprobenergebnisse Xi bezeichnet, mit der man auf den entsprechenden Parameter Θ der Grundgesamtheit schließt:
T ⇒ Θ .
Dies impliziert, dass es verschiedene Möglichkeiten gibt, diese Schätzfunktion zu definieren.
Bezüglich der Schätzung von σ stehen uns z. B. zwei Standardabweichungen zur Verfügung: s und ŝ. Dass im Mittelwert-Test auf letztere zurück gegriffen wurde, deutet daraufhin, dass diese Größe der bessere Schätzer ist.
Auch eine Schätzung von μ könnte sich z. B. auf das arithmetische Mittel X̄, den Median MED oder den Modus MOD einer Stichprobe stützen. Bei einer Festlegung des Stichprobenumfangs auf n = 1 könnte sogar ein einzelner Stichproben-Wert Xi zu Grunde gelegt werden.
Die Frage ist also, welcher der o. a. Schätzer der tauglichste ist. Dazu gibt es Kriterien und Verfahren, um die Schätzfunktion zu optimieren und die Gefahr von Fehlschlüssen zu verringern.
b) Die Schätzkriterien
Das wichtigste Schätzkriterium ist die Erwartungstreue. Damit erwarten wir, dass der Schätzer unverzerrt (unbiased) ist, d.h. im Schnitt den wahren Parameter trifft. Allgemein gilt für die Erwartungstreue des Schätzers:
E(T) = Θ
Bei nicht symmetrischen Verteilungen sind z. B. der Median und der Modus keine erwartungstreue Schätzer für μ, wohl aber X̄ und Xi, weil sowohl E(X̄)= μ wie E(Xi) = μ.
Ein weiteres Kriterium ist die Konsistenz. Diese ist dann gegeben, wenn sich bei wachsendem Stichprobenumfang T und Θ annähern und bei n = N übereinstimmen. Für eine Schätzung von μ wäre also X̄ ein konsistenter Schätzer, nicht aber Xi, weil ein einzelner Wert Xi von n unabhängig ist.
Schließlich ist als weiteres wichtiges Kriterium die Effizienz einer Schätzfunktion zu nennen. Relativ effizient ist eine Schätzfunktion, wenn ihre Varianz kleiner ist als die einer anderen, also wenn gilt:
VAR(T1) < VAR(T2).
Ist eine relativ effiziente Schätzfunktion auch erwartungstreu, spricht man von absoluter Effizienz.
c) Die Schätzmethoden
Zur konkreten Ableitung der der Schätzfunktionen stehe zwei Verfahren (mit meist identischen Ergebnisse) zur Verfügung, die hier nur kurz angesprochen werden sollen:
Die maximum-likelihood-Methode (Methode der maximalen Mutmaßlichkeit) konstruiert die Schätzfunktion so, dass der Schätzer Θ̄ den gegebenen Stichproben-Werten X1 . . . Xn die größte Mutmaßlichkeit L zuweist:
L(Θ̄ | X1 . . . Xn) = max!
Die Methode der kleinsten Quadrate ermittelt den Schätzer Θ̄ so, dass
∑(Θ̄ - T) ² = min !
2. Die Intervallschätzung
a) Die Ausgangslage
-
Die Punkthypothese postuliert, dass der Parameter der Grundgesamt einen genau bestimmten Wert hat. Diese Aussage ist bereits falsch, wenn der Parameter nur knapp über oder unter dem ermittelten Wert (X̄, p oder ŝ) liegt. Dass sie also richtig ist, trifft in den seltensten Fällen zu. Dazu kommt in der Praxis, dass eine genaue Positionsbestimmung meist gar nicht notwendig ist. Wie bereits festgestellt, nimmt die Treffsicherheit der Aussage zu, je größer der Bereich ist. Im Extremfall liegt man immer richtig mit der Aussage, der Parameter liege im Intervall ±∞. Welche Treffsicherheiten sind also letztlich sinnvoll und wie lassen sich die Intervallgrenzen bestimmen?
Die Intervallschätzung stützt sich wie die Punktschätzung auf die entsprechende Stichprobenstatistik. Deshalb basieren die Ableitung der Intervallgrenzen wieder auf den
Stichprobenverteilungen der X̄, ŝ und p
.
Das Intervall wird durch eine Ober- und eine Untergrenze begrenzt, deren Werte über die Stichprobenstatistiken bestimmt werden.
Es liegt auf der Hand, bei der Ermittlung der Intervalle mit den gleichen Wahrscheinlichkeitskonzepten zu arbeiten wie beim Hypothesentest. Nur bezieht man diese jetzt nicht auf das Signifikanzniveau α, das ja die Randbereiche definiert, sonder auf das Konfidenzniveau 1 - α, weil nun die
inneren Bereiche der Wahrscheinlichkeitsverteilungen abgegrenzt werden sollen. Gängige Werte sind 90%, 95% und 99%, d. h. 1 - α = 0.90, 0.95 oder 0.99.
Ein häufig zu findender Trugschluss betrifft dabei den Begriff des Vertrauens- bzw. Konfidenzniveaus. Wurde ein 95%-Intervall gewählt, so wäre es falsch zu sagen, der Parameter der Grundgesamtheit liegt mit einer Wahrscheinlichkeit von 95% in dem ermittelten Intervall! Je nach gezogener Stichprobe liegt der Parameter entweder in dem Intervall oder er liegt nicht darin! Korrekt ist hingegen die Aussage, dass der Parameter in 95% aller Fälle in dem Intervall liegt (vgl. dazu Abb. V-3 im folgenden Modul). Man spricht deshalb von einer Konfidenz oder Mutmaßlichkeit von 95%, dafür dass der Parameter im ermittelten Intervall liegt.
Das Konzept des Konfidenzintervalls oder Vertrauensbereichs soll im Folgenden am Beispiel einer Konfidenzschätzung für den Mittelwert μ der Grundgesamtheit entwickelt werden. Ausgangspunkt ist dabei die Stichprobenverteilung des arithmetischen Mittels X̄.
b) Das Konzept des Konfidenzintervalls am Beispiel des Mittelwerts μ
-
Ein erste Überlegung zur Ermittlung der Intervallgrenzen könnte sich unmittelbar auf den Hypothesentest beziehen. So wäre zu fragen, ob nicht die Spannweite des Intervalls identisch sein sollte mit alternativen Hypothesen für den Parameter der Grundgesamtheit H0: μ = μ0 und H0: μ = μ1, die beide mit dem realisierten Stichprobenergebnis X̄ gerade noch kompatibel sind (vgl. Abb. V-1):
Abb. V-1 Konfidenzbereich für μ
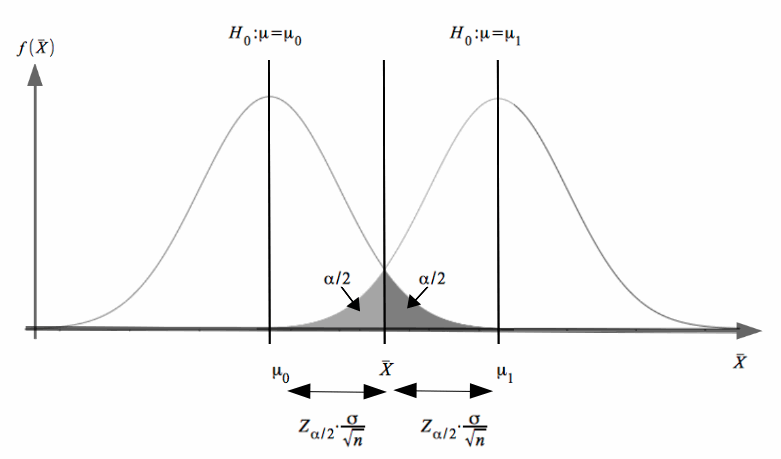
Im beidseitigen Test der Punkthypothese μ = μ0 liegt X̄ bei einem Signifikanzniveau von α0 genau auf der oberen Grenze des Annahmebereichs.
-
Gleichzeitig liegt X̄ genau auf der unteren Grenze des Annahmebereichs der Punkthypothese μ = μ1.
-
In Konsequenz dieser Abschätzung erhalten wir bei gegebenem Konfidenzniveau 1 - α einen Vertrauensbereich, der genau so groß ist wie der Annahmebereich einer Punkthypothese bei entsprechendem Signifikanzniveau α.
-
Vergrößert man α und verringert damit das Intervall, erhält man eine präzisere Aussage. Jedoch ist dann diese Aussage unsicherer.
c) Die Berechnung des Konfidenzintervalls für den Mittelwert μ
-
Bei der Punkthypothese beträgt der Abstand zwischen dem hypothetischen Wert μ0 zur oberen und bei μ1 zur unteren Grenze jeweils 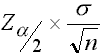 (vgl. Abb. V-1). Damit ergibt sich als Konfidenzintervall μ˜ eine Spanne (vgl. Abb. V-1). Damit ergibt sich als Konfidenzintervall μ˜ eine Spanne
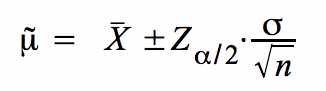
Eine ausführliche Ableitung der Formel wird im folgenden Modul präsentiert.
-
Zur Erinnerung: Der Annahmebereich für die Punkthypothese lautete:
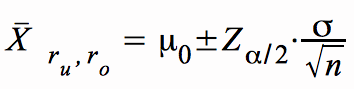
Beide Formel unterscheiden sich nur bezüglich der Positionen von μ und X̄. Somit zeigt sich auch in den Berechnungsformeln die Analogie zwischen Hypothesentest und Konfidenzschätzung.
d) Die Wahl des Stichprobenumfangs
-
Eine genauere Verortung des Parameters der Grundgesamtheit bei gleicher Präzision ist über eine Vergrößerung der Stichprobe zu erreichen. An der Abb. V-1 ist kann nachvollzogen werden, dass die Streuung der Verteilung mit dem Stichprobenumfang n variiert, d. h. je größer n, desto schmaler sind die Stichprobenverteilungen und desto kleiner das Intervall. In der Berechnungsformel für ˜μ macht sich dieser Sachverhalt dadurch bemerkbar, dass n als Wurzel im Nenner steht.
-
Die Spanne zwischen der Grenze des Konfidenzintervalls und der Stichprobenstatistik wird als Stichprobenfehler bezeichnet. Seine Abhängigkeit von n erlaubte es, ihn durch entsprechende Wahl von n zu begrenzen. Die Ermittlung des optimalen Stichprobenumfangs wird im letzten Modul diese Kapitels vorgestellt.
|



