Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

Bei einer Punktschätzung wird von den Sichprobenstatistiken unmittelbar auf den entsprechenden Paramter der Grundgesamtheit geschlossen. Damit hat man zwar eine punktgenaue Aussage, trifft diese aber mit einem hohen Risiko.

Die Intervallschätzung räumt bereits von vornherein einen gewissen Stichprobenfehler ein. Somit suchen wir nach einem Bereich (Konfidenzintervall, Vertrauensbereich), in dem der Parameter liegt. Für eine solche Schätzung benötigen wir zunächst die Größe des Vertrauensniveau, gängige Werte sind 90%, 95% und 99%. Das Intervall wird durch eine Ober- und eine Untergrenze begrenzt. Wird z.B. ein 95%-Intervall gewählt, überdeckt dieses Intervall in 95% aller Konfidenzschlüsse den wahren Parameter.

Ein häufig zu findender Trugschluss betrifft den Begriff des Vertrauens- bzw. Konfidenzniveaus. Wurde ein 95%-Intervall gewählt, liegt der Parameter nicht mit einer Wahrscheinlichkeit von 95% in dem Intervall! Je nach gezogener Stichprobe liegt der Parameter entweder in dem Intervall oder nicht! Korrekt ist jedoch die Behauptung, dass in 95% aller Fälle der Parameter in dem Intervall liegt.

Das allgemeine Konfidenzniveau soll im Folgenden am Beispiel einer Konfidenzschätzugn für den Mittelwert der Grundgesamtheit entwickelt werden. Ausgangspunkt ist wieder die Stichprobenverteilung der arithmetischen Mittel (vgl. obere Grafik). Alle Stichprobenmittelwerte, die in den schraffierten 95%-Bereich fallen, konstituieren Schätzintervalle der Breite des schraffierten Bereichs, in denen mit Sicherheit der wahre Parameter der Grundgesamtheit liegt (vgl. untere Grafik):

In der folgenden Darstellung sind drei mögliche Stichprobe eingezeichnet:

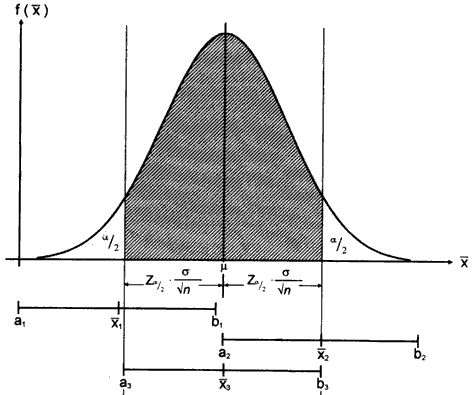
Wie man sieht, enthalten die Intervalle um 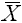mit der Breite +/- 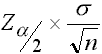der Stichprobe 2 und 3 den Wert Grundgesamtheit. Das Intervall der Stichprobe 1 enthält ihn nicht.

Je größer der Stichprobenumfang n, desto schmaler wird die Stichprobenverteilung und damit das Intervall. Vergrößert man (und verringert damit das Intervall) und hält n konstant, erhält man ebenfalls engere Intervalle. Jedoch ist dann die Aussage unsicherer.

Konfidenzintervalle für Mittelwerte

Wie "gut" oder "schlecht" Schätzungen sein können, zeigt dieses Skript. Es zieht aus einer Grundgesamtheit sechs Stichproben und zeigt an, ob der Paramter der GG von dem Intervall überdeckt ist. (Weitere Informationen auf der Seite.)

Ein weiteres Simulationsprogramm der Rice University erlaubt die Berechnung und graphische Darstellung von Konfidenzintervallen für den Mittelwert und den Anteilswert bei unterschiedlichen Stichprobengrößen.

letzte Änderung am 5.4.2019 um 4:24 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel04_Konfidenzintervalle/modul01_Das~~lallgemeine~~lSch~~aetzmodell/ebene01_Konzepte~~lund~~lDefinitionen/04__
01__01__01.php3