 |
Beispiele und Aufgaben im Modul Test des Anteilswertes
1. Beispiele
a) Beispiel für Hypothesentests auf der Basis n · π (1- π) ≤ 9
Beispiele für Hypothesentests bei kleine Stichproben wurden bereits im vorangegangenen
Modul (Punkt 1 c und d) sowohl für Punkt- wie für Bereichshypothesen vorgestellt. Die Berechnungen von Grenzen für Annahme- und Ablehnungsbereiche basierten auf einer Stichprobe mit n = 20 und einem π von 0,7 und wurden tabellarisch und graphisch veranschaulicht.
b) Beispiel für Hypothesentests auf der Basis n · π (1- π) > 9
Ein Internetprovider plant eine spezielle Werbekampagne in Regionen mit einer unterdurchschnittlichen Internetnutzung. Kriterium soll ein Anteil von höchstens 70% Haushalten mit Netzzugang sein. Zur Auswahl passender Regionen führt er jeweils Zufalls-Stichproben im Umfang von n = 100 Haushalten durch.
Prüfen Sie, ob die Voraussetzungen für die Normalverteilung vorliegt und bestimmen Sie die Parameter dieser Verteilung. Welche Hypothese würde ein eher risikofreudiger, welche ein eher vorsichtiger Anbieter formulieren. Ermitteln Sie die Annahme- bzw. Ablehnungsbereiche, die jeweils zum Start der Werbekampagne führen. Welche Schlussfolgerungen hinsichtlich einer Annahme oder Ablehnung der Hypothesen ergeben sich nach Ziehung der Stichprobe aus einem Anteilswert p = 0,68?
ad 1: Die Verteilung des Stichprobenparameters
Wir prüfen zuerst, ob die diskrete Binomial-Verteilung der Variablen hinreichend durch eine Normalverteilung approximiert werden kann. Die Approximationsbedingung lautet:
n · π(1-π) ≥ 9, konkret: 100 · 0.7(1-0.7)= 21 ≥ 9. Damit ist die Bedingung erfüllt.
Da die Anzahl der Haushalte in den ins Auge gefassten Regionen über 2000 liegt, kann der Endlichkeitsfaktor auf "1" gesetzt werden.
Wir ermitteln danach die Parameter der Normalverteilung: p hat einen Erwartungswert
E(p) = π = 0.7 und eine Varianz
VAR(p) = π(1-π)/n = 0.7(1- 0.7)/100 = 0.0021.
Da n ≤ 1000 ist die Steigkeitskorrektur zu berücksichtigen.
-
Ein Signifikanzniveau von 0,01 ergibt für einen einseitigen Test einen Z α-Wert von 2,33 (vgl. die Werte in dieser Übersicht).
ad 2: Die Formulierung der Hypothesen
Ein risikofreudiger Anbieter würde die Hypothese formulieren: H 0: π ≤ π 0 .
Diese führt zu einem rechtsseitigen Test mit einem Ablehnungsbereich P( Z ≥ Z r o) = α 0,
woraus sich folgender oberer Zurückweisungspunkt ergibt:
.gif)
Der Anbieter würde also die Kampagne starten, auch wenn der Stichprobenanteilswert über dem hypothetischen Wert π 0, aber noch unter dem Zurückweisungspunkt p o liegt.
Ein vorsichtiger Anbieter würde die Gegenhypothese formulieren: H 0: π ≥ π 0.
und die Kampagne starten, wenn diese Hypothese zu widerlegen ist. Dieser Ansatz führt zu einem linksseitigen Test mit einem Ablehnungsbereich
P( Z ≤ Z ru ) = α 0,
woraus sich folgender unterer Zurückweisungspunkt ergibt:
.gif)
D.h. das Stichprobenanteilswert p müsste schon deutlich unter π 0 liegen, bevor die Werbekampagne durchgeführt wird.
ad 3: Die Berechnung der Grenzen
Die Hypothese : H 0: π ≤ π 0
führt zu einem rechtsseitigen Test mit einem Ablehnungsbereich P( Z ≥ Z r o) = α 0,
und dem oberen Zurückweisungspunkt:
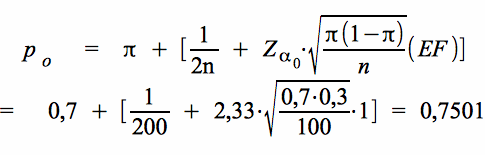
Die Gegenhypothese H 0: π ≥ π 0.
führt zu einem linksseitigen Test mit einem Ablehnungsbereich
P( Z ≤ Z ru ) = α 0 und dem
unteren Zurückweisungspunkt:
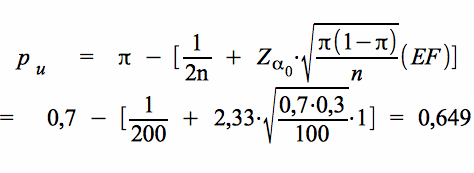
ad 4: Die Konsequenzen des Testergebnisses
Ein p = 0,068 in der Stichprobe führt dazu, dass beide Hypothesen anzunehmen sind. Ein risikofreudiger Anbieter würde in diesem Falle die Kampagne starten, ein risikoscheuer würde zögern. Er wird erst dann eine Kampagne durchführen, wenn der Anteilswert in der Stichprobe unter 0,65 liegt. Diese nicht eindeutigen Situation lässt sich u.U. dadurch auflösen, eine weitere Stichprobe mit einem größeren Umfang zu ziehen.
2. Aufgaben
Über "Abschicken" kommen Sie zur Bearbeitung des zweiten Schrittes.
b) Lösungsvariante 2
Hinweis: Bestimmen Sie je nach Aufgabenstellung den unteren und/oder oberen Grenzwert des Annahmebereichs der jeweiligen Hypothese. Setzen Sie dazu die passenden Werte in die Felder der Formeln ein. Nicht benötigte Felder lassen Sie unverändert.
Die Aufgabe 35 ist
hier in sechs Schritten zu lösen! Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
Eine ausführliche Darstellung der Lösung von Aufgabe (35) finden Sie im Link am Ende des Kapitels.
Aufgabe 36
Partei A will herausfinden, wie bei der Kommunalwahl in der Stadt B (50.000 WählerInnen) ihre Chancen zur Überwindung der 5%-Grenze stehen.
Von 15 zufällig ausgewählten WählerInnen einer Stichprobe würde keiner die Partei A wählen. Formulieren Sie die Nullhypothese, dass A die 5%-Hürde überwinden wird, und testen Sie diese mit einem Signifikanzniveau von 10%! Welchen Rat würden Sie der Partei geben?
Die Aufgabe 36a ist
hier in sechs Schritten zu lösen! Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
A fühlt sich durch das Ergebnis des ersten Tests ermutigt und möchte nun mit einer zweiten, größeren Umfrage noch etwas genauer abschätzen lassen, ob sie mindestens die 5%-Grenze erreicht. Das von A beauftragte Meinungsforschungsinstitut M führt eine Umfrage mit n = 2000 durch. 80 WählerInnen geben an, A wählen zu wollen. Testen Sie mit einem 5% Signifikanzniveau die obige Hypothese und bewerten Sie das Ergebnis.
Die Aufgabe 36b ist
hier in sechs Schritten zu lösen!
Welches Ergebnis resultiert aus der Veränderung des Signifikanzniveaus auf 0,01?
Die Aufgabe 36c ist
hier in zwei Schritten zu lösen!
Wenn die Partei sicher sein möchte, in den Stadtrat zu kommen, sollte sie die entsprechende Gegenhypothese überprüfen. Wie viel % der Wähler müssten sich dann in einer 2000er-Stichprobe mindestens für A aussprechen, damit sie diese Hypothese ablehnen kann? (Signifikanzniveau: d-1: 5% und d-2: 1%).
Die Aufgabe 36d ist
hier in vier Schritten zu lösen!
Diskutieren Sie anhand der Teilaufgaben b), c) und d) die Problematik der Festlegung der Testhypothese und des Signifikanzniveaus.
Die Aufgabe 36e wird hier diskutiert!
|



