Die Ausgangsdaten
Die Kompetenz einer Partei im Bereich „Allgemeine Sicherheit“ wurde in der Vergangenheit auf einer Skala von 0 – 10 durchschnittlich mit 6,7 Punkten bewertet. Nach einer kontroversen Parlamentsdebatte soll die Hypothese getestet werden, die Glaubwürdigkeit der Partei sei danach unverändert, wenn nicht sogar gestiegen. In einer Blitzumfrage mit n = 100 ergibt sich ein durchschnittlicher Punktewert von 6,35 bei einer Standardabweichung ŝ von 1,2 Punkten.
Die Testvorgaben
Mit Hilfe des Hypothesen-Tests soll nun überprüft werden, ob sich die durchschnittliche Glaubwürdigkeit wirklich erhöht oder nicht doch verringert hat. Die möglichen Hypothesen lauten:
H0: μ ≥ μ0 (die Glaubwürdigkeit ist jetzt gleich oder größer)
H0: μ < μ0 (die Glaubwürdigkeit ist jetzt geringer)
Die Partei entscheidet sich dafür, die optimistische Hypothese mit einem Signifikanzniveau α0 von 5 % zu testen.
Prüfung der Voraussetzungen
Auf den Endlichkeitsfaktor können wir bei dieser Aufgabe verzichten.
Ermittlung des (Zα0)-Werts
Zur Durchführung des Tests benötigen wir den Z-Wert (Zα0), der sich für das gewählte α0 = 0,05 ergibt. Aus der Tabelle erhalten wir: (Zα0) = -1,65.
Durchführung des Tests
Wir führen den Test nun beispielhaft in drei äquivalenten Varianten durch:
Vergleich der Z-Werte
Mit Hilfe der Z-Transformation berechnen wir den Z-Wert, der sich aus den Angaben ergibt:
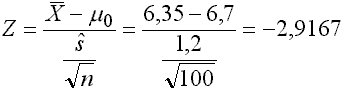
Der empirische Z-Wert liegt, wie die linke Seite der Abbildung IV-5 zeigt, im Ablehnungsbereich.
Vergleich der X̄-Werte
Rechnet man die Aufgabe mit der nach X̄ aufgelösten Z-Transformationsformel, erhält man:
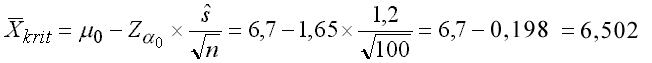
Hier liegt nun das empirische X̄ im Ablehnungsbereich (vgl. rechte Seite der Abb. IV-5).
Abb. IV-5 Annahme- und Ablehnungsbereiche für Z und für X̄
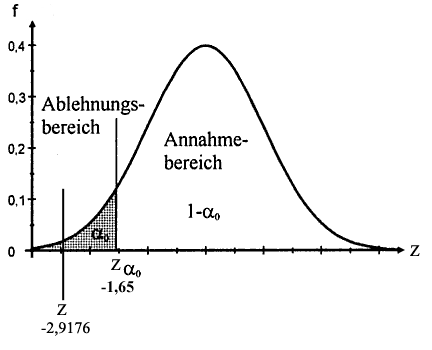
P( Z ≤ - 1,65) = 0,05 | 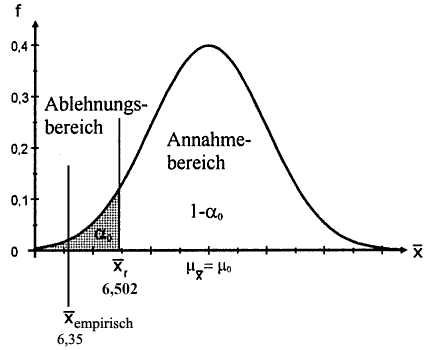
P( X̄ ≤ 6,502) = 0,05 |
Vergleich der α-Werte
Alternativ zu den beiden Rechnungen unter 1. und 2. können wir für den unter 1. errechneten empirischen Z-Wert von -2,9167 in der Tabelle das ihm entsprechende empirische α ermitteln und mit α0 vergleichen. Dem Z-Wert von -2,9167 entspricht ein α von 0,00175. Dieser Wert ist wesentlich kleiner als 0,05, was ebenfalls zur Ablehnung der Hypothese führt (vgl. dazu Abb. IV-5 linke Graphik).
Ergebnis des Tests
Nach allen Rechnungsvarianten muss also die H0 zugunsten der H1 verworfen werden, Somit kann behauptet werden, dass sich die Glaubwürdigkeit mit einer Signifikanz von 5% verringert hat.
Modifikation der Testvorgaben
Hätte die Partei nicht die optimistische Hypothese sondern die Gegenhypothese getestet, wäre es bei obigen Stichprobenwerten natürlich zu einer eindeutigen Zustimmung zur pessimistischen Varianten gekommen.



