 |
Regressionsanlytische Tests mit SPSS - Beispiele und Aufgaben im Modul IV-6 Test der Regressions- und des Korrelationskoeffizienten
Teil A: Beispiele und Aufgaben zur einfachen Regressions- und Korrelationsanalyse
1. Test der Regressionsfunktion mit SPSS
In ViLeS 1 war am Beispiel der Datei Partizipation.sav eine einfache Regressions- und Korrelationsanalyse der Beziehung zwischen der tatsächlichen Beteiligung an betrieblichen Entscheidungsprozessen (Variable Partizipationsprofil) und der gewünschten Beteiligung (Variable Partizipationspotential) mit SPSS durchgeführt worden (vgl.: Regressionsanalyse mit SPSS ).
In ViLeS 1 konnten die induktiven Aspekte der Analyseergebnisse noch nicht interpretiert werden. Dies soll nun erfolgen. Wir betrachten dazu die Testergebnisse für A und B, die in Tab. IV-16 nochmals dargestellt werden.
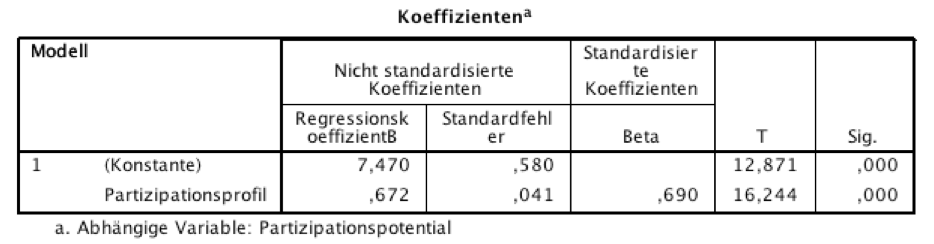
Tab. IV-16 Ergebnisse zur Regression zwischen Partprof und Partpot
a) Der Test von H0: A = A0
Im Folgenden beziehen wir uns auf die Werte in der ersten Zeile in der obigen Tabelle, die die Regressionskonstante a = 7,47, den Standardfehler der Regressionskonstanten ŝa = 0,58, den T-Wert T = 12,871 und dessen Signifikanz von 0,000 beinhalten. Die Testprozedur umfasst folgende Aspekte:
Die Formulierung der Null-Hypothese und die Festlegung des Signifikanzniveaus:
Die von SPSS durchgeführten Hypothesentests formulieren als Null-Hypothese generell, dass die Regressionsparameter in der Grundgesamtheit die Werte "Null" aufweisen. Hier lautet die Hypothese zu A also konkret:
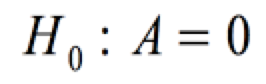
Diese Hypothese soll auf der Basis einer t-Verteilung mit einem Signifikanzniveau von α = 0,05 getestet werden.
Die Berechnung von T (vgl. Tab. IV-16)
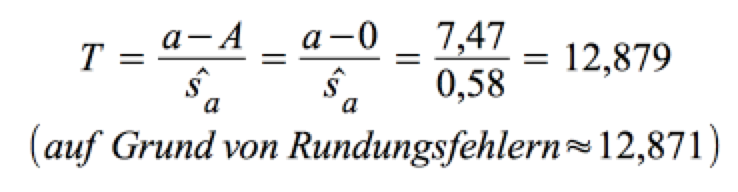
Die Interpretation von Sig. = 0,000
Dieses Testergebnis spiegelt den Testansatz von SPSS wieder, bei dem die Wahrscheinlichkeit Sig. ausgewiesen wird mit:
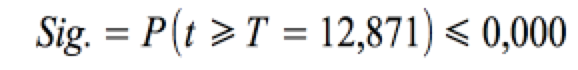
Die Null-Hypothese wird wird bei den gegebenen Freiheitsgraden von FG = n-2 = 290 in einem zweiseitigen Test und einem Signifikanzniveau α = 0,05 verworfen, weil Sig. = 0,000 ≤ 0,025 .
b) Der Test von H0: B = B0
Im Test des Regressionskoeffizienten beziehen wir uns auf die Werte in der zweiten Zeile in der Tabelle IV-16: auf den Regressionskoeffizienten b = 0,672, den Standardfehler des Regressionskoeffizienten ŝb = 0,041, dessen T-Wert T = 16,244 und dessen Signifikanz von 0,000. Die Testprozedur besteht wieder aus folgenden Komponenten:
Die Formulierung der Null-Hypothese und die Festlegung des Signifikanzniveaus:
Die Hypothese:
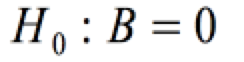
soll wieder mit einem Signifikanzniveau von α = 0,05 getestet werden.
Die Berechnung von T (vgl. Tab. IV-16)
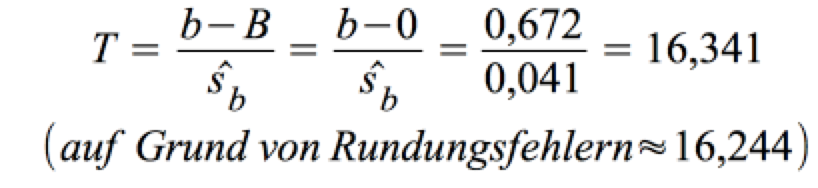
Die Interpretation von Sig. = 0,000
Im Testansatz von SPSS wird die Null-Hypothese bei einem zweiseitigen Test und einem Signifikanzniveau α = 0,05 verworfen, wenn Sig. ≤ 0,025:
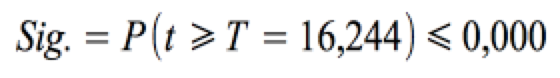
Die Null-Hypothese wird wird bei den gegebenen Freiheitsgraden von FG = n-2 = 290 in einem zweiseitigen Test und einem Signifikanzniveau α = 0,05 verworfen, weil Sig. = 0,000 ≤ 0,025 .
2. Test des Determinationskoeffizienten mit SPSS
a) Die Korrelationsergebnisse
|
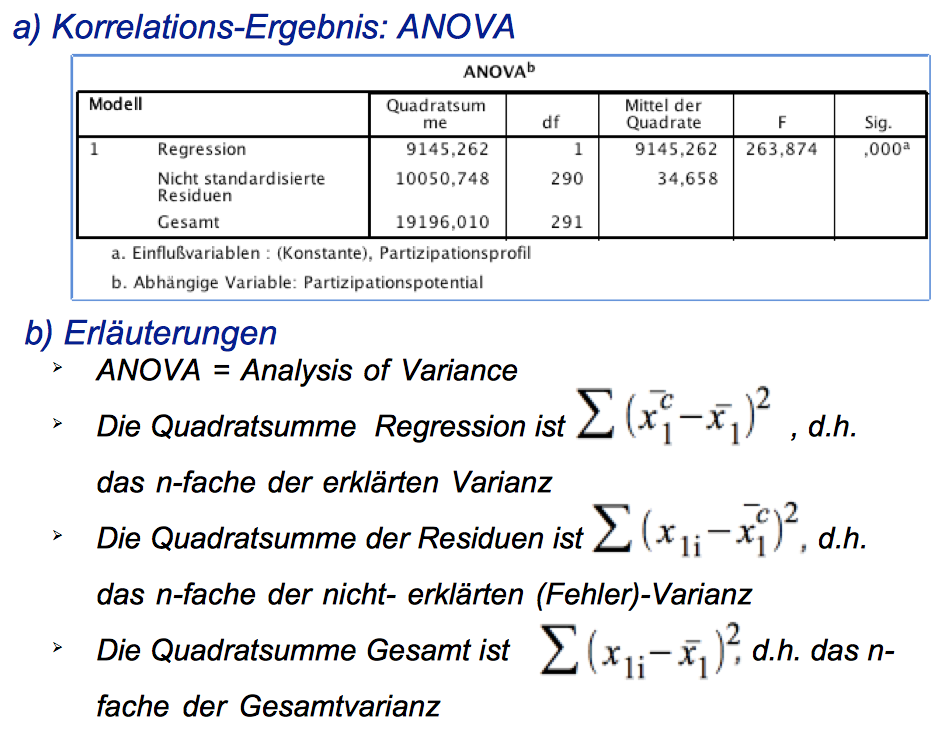
Screenshot IV-1: Die ANOVA-Ergebnisse der Korrelationsanalyse
|
| Screenshot IV-2: Die Maßzahlen der Korrelationsanalyse

|
In den beiden Tabellen besteht folgende Beziehungen zwischen dem Mittel der nicht-standardisierten Residuen und dem Standardfehler des Schätzers:
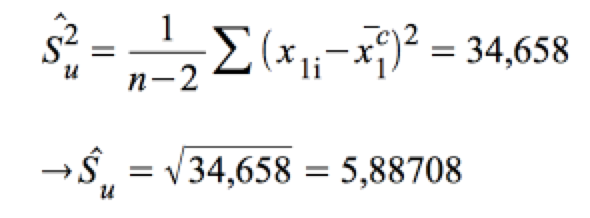
b) Der Test von H0: ρ2 = ρ20
Im Folgenden beziehen wir uns auf die Werte in den obigen Tabelle, insbesondere auf die verschiedenen Quadratsummen (SAQ-Werte), die beiden R2-Werte sowie den Standardfehler des Schätzers ŝu = 5,89, den F-Wert F = 263,874 und dessen Signifikanz von 0,000.
Die Testprozedur umfasst wieder folgende Aspekte:
Die Formulierung der Null-Hypothese und die Festlegung des Signifikanzniveaus:
Der von SPSS durchgeführte Hypothesentest formulieren als Null-Hypothese, dass die Korrelationsparameter in der Grundgesamtheit die Werte "Null" aufweisen, konkret also:
H0: ρ2 = ρ20 .
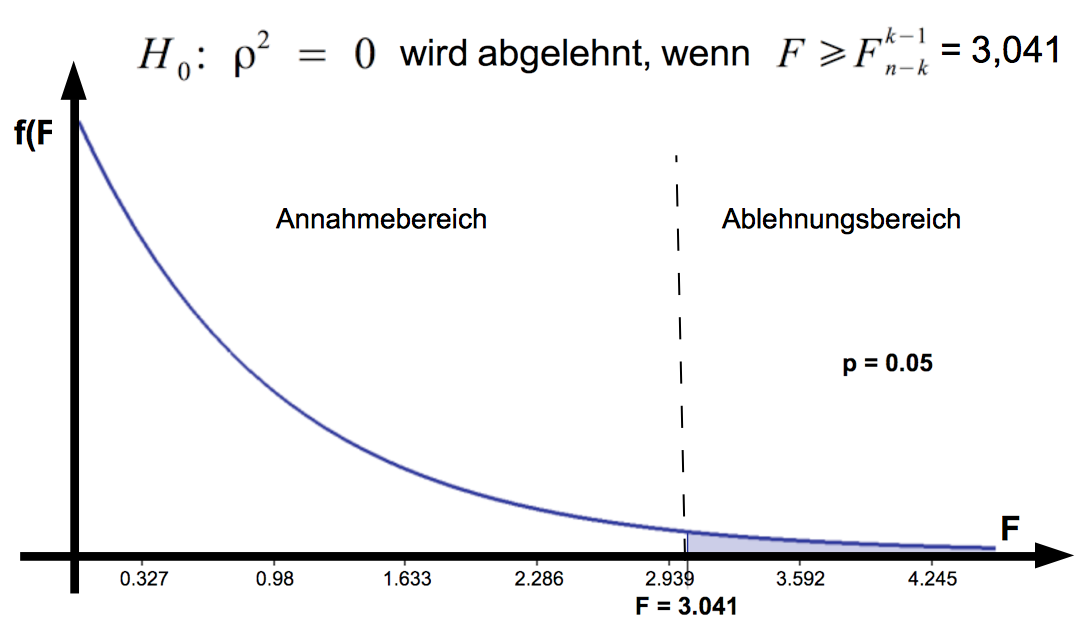
Die Ermittlung der Annahme- und Ablehnungsbereiche
Bei den gegebenen Freiheitsgraden von FGReg (dfReg = k - 1 = 2 -1) und FGRes (dfRes = n - k = 292 - 2) erhalten wir für die Testgröße F
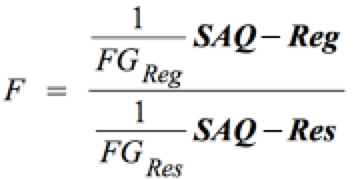
die folgenden Annahme- und Ablehnungsbereiche:
Abb. IV-28: Annahme- und Ablehnungsbereiche für die Nullhypothese
Die Berechnung von F
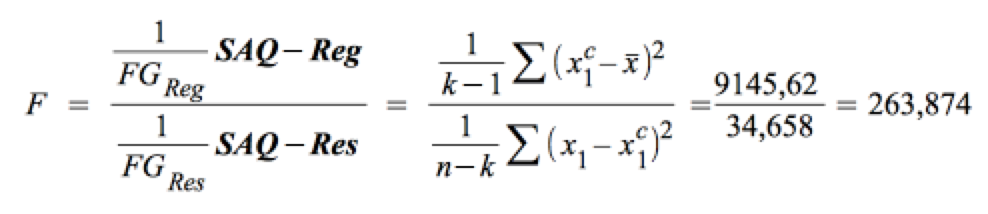
Damit liegt F überdeutlich im Ablehnungsbereich der Hypothese.
Die Interpretation von Sig = 0,000
Dieses Testergebnis spiegelt den Testansatz von SPSS wieder, bei dem die Wahrscheinlichkeit Sig. ausgewiesen wird mit:
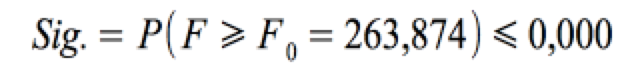
Die Null-Hypothese wird wird bei einem einseitigen Test und einem Signifikanzniveau α = 0,05 verworfen, wenn Sig. ≤ 0,05.
Ein Test auf der Basis der t-Verteilung
Bei FGReg = 1 und FGRes = 290 kann über √ F = t der Test auch über die t- (bez. Normal-)Verteilung durchgeführt werden.
Dazu ergeben sich die Annahme- und Ablehnungsbereiche, wie in Abb. IV-29 dargestellt.
Die Hypothese wird abgelehnt, wenn:
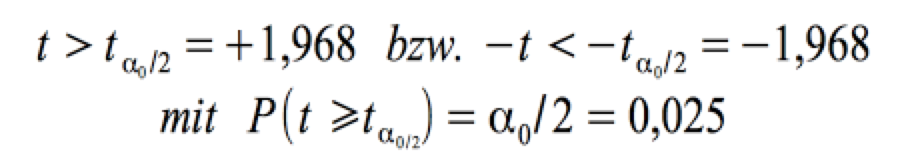
Aufgrund von t = √ F = √ 263,874 = 16,244 > 1,968 , wird auch nach dieser Testvariante die Null-Hypothese abgelehnt.
3. Aufgaben zum Test der Ergebnisse des Regressions- und Korrelationsmodells
a) Aufgaben zum Test der Regressionsfunktion
Testen Sie die folgenden Hypothesen zu den Ergebnissen der vorangehend diskutierten Regressionsanalyse.
Bei n= 292, können Sie den Stichprobenverteilungen der Parameter eine Normalverteilung zugrunde legen!
b) Aufgaben zum Test der Korrelation
Testen Sie die Hypothese ρ20 = 0,5 mit der im Abschnitt 3. des vorangegangenen Modul dargestellten Fisher's Z-Transformation.
|



