 |
Konzepte und Definitionen im Modul IV-6 Test der Regressions- und des Korrelationskoeffizienten
Teil B: Die Tests der partiellen/multiplen Regressions-und Korrelationskoeffizienten
Vorbemerkungen
In diesem Abschnitt werden Verfahren diskutiert, mit denen von den empirischen Regressions- und Korrelationsergebnissen einer Stichprobe auf die entsprechenden Zusammenhänge in der Grundgesamtheit geschlossen werden kann.
Diese Ergebnisse basieren auf den partiellen bzw. multiplen Regressions- und Korrelationsmodellen, die auf der Plattform-Komponenten
"ViLeS 1"
im Modul
Multiple Regressions- und Korrelationsmodelle vorgestellt wurden.
Aus ViLeS 1 ist bekannt, dass die multiplen Regressionskoeffizienten den partiellen/semipartiellen Regressionskoeffizienten entsprechen.
1. Der Test der multiplen Regressionskoeffizienten
Mit dem Hypothesentest wird die Signifikanz der einzelnen partiellen Regressionskoeffizienten geprüft, d.h. geklärt, ob die festgestellten Wirkungen der jeweiligen unabhängigen Variablen auch für die Grundgesamtheit anzunehmen sind oder doch nur zufällig vorgefunden wurden.
a) Die Verteilung der partiellen Regressionskoeffizienten
Wir betrachten dazu die Verteilung der partiellen Regressionsparameter b*j bei unendlich vielen Stichproben:
Abb. IV-27: Die Stichprobenverteilung der b*j
Der Erwartungswert des Koeffizienten b*j entspricht dem Parameter der Grundgesamtheit B*j :
Seine Standardabweichung ist gegeben mit:
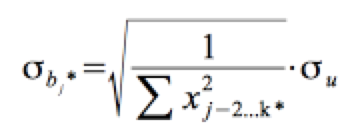
Die Standardabweichung der Fehler in der Grundgesamtheit σu wird geschätzt über den Standardfehler des Schätzers sˆu . Daraus resultiert der Standardfehler der Koeffizienten:
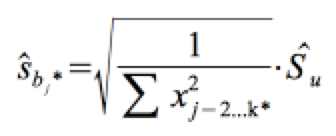
b) Das Testverfahren
Getestet wird nun die Hypothese H0, dass die partiellen Regressionskoeffizienten
der Grundgesamtheit A* und B*2....B*k jeweils Null sind:
Der Test basiert auf der t-verteilten Teststatistik t0:
Bei positiven Werten von b*j ergeben sich für die Hypothese die in Teil A dargestellten Annahme- und Ablehnungsbereiche auf der Basis der t-Verteilung:
Abb. IV-24: Die Grenzen des Annahmebereichs auf der Basis der t-Verteilung
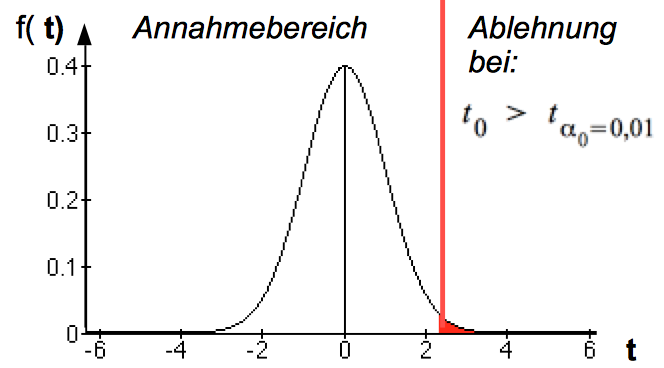
tα0 ergibt sich bei φ = n - k Freiheitsgraden und einem Signifikanzniveau von α0 aus der Tabelle oder einem Rechner.
Alternativ kann die Nullhypothese zurückgewiesen werden, wenn die für t0 berechnete Signifikanz von α < 0,01 bzw. < 0,05 ist.
Bei negativen Werten von b*j ergibt sich der Ablehnungsbereich für die Hypothese mit t < -tα0 .
2. Die Tests der multiplen Determinationskoeffizienten
a) Der Test des Gesamtmodells
Die Hypothese lautet, dass der Determinationskoeffizient der Grundgesamtheit Null ist:
Diese Hypothese wird mittels der F-Verteilung getestet und abgelehnt, wenn 
Abb. IV-28: Annahme- und Ablehnungsbereiche für F
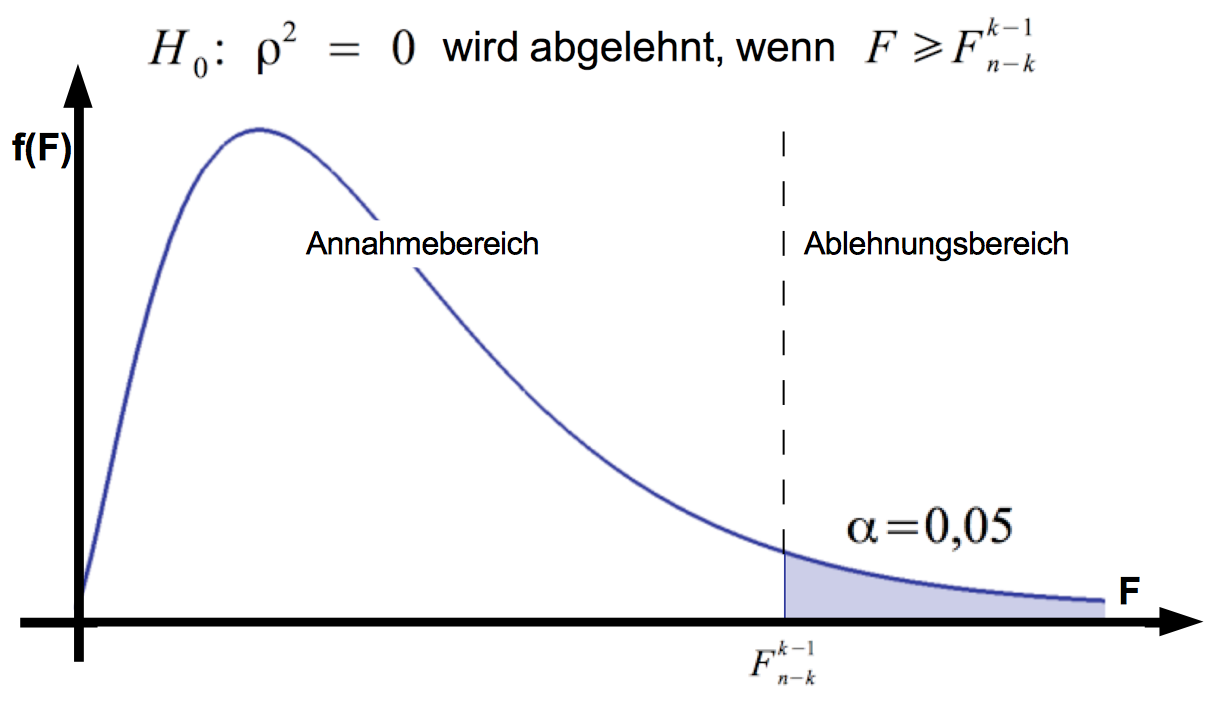
F0 ist als Verhältnis der, mit den jeweiligen Freiheitsgraden gewichteten, erklärten Gesamtsumme der Abstandsquadrate zur nicht-erklärten Gesamtsumme der Abstandsquadrate definiert:
 ergibt sich bei k-1 Zählerfreiheitsgraden und n-k Nennerfreiheitsgraden bei gewähltem Signifikanzniveau von Α aus der Tabelle oder über den Rechner.
Alternativ kann die Nullhypothese zurückgewiesen werden, wenn der berechnete Wert F0 < 0,01 bzw. < 0,05 ist.
tα0 ergibt sich bei φ = n - 2 Freiheitsgraden und einem Signifikanzniveau von α0 aus der Tabelle oder einem Rechner.
Alternativ kann die Nullhypothese zurückgewiesen werden, wenn die für t0 berechnete Signifikanz von α < 0,01 bzw. < 0,05 ist.
Bei negativen Werten von b ergibt sich der Ablehnungsbereich für die Hypothese mit t < -tα0 .
b) Der schrittweise Test der Modellkomponenten
Der schrittweise Test beinhaltet den Test der zuletzt aufgenommenen Variablen xk*
Die Hypothese
wird angenommen, wenn:
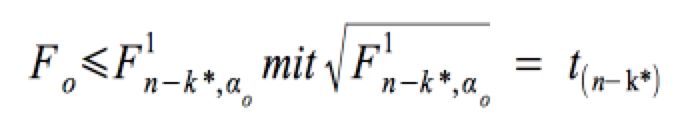
entspricht bei k* = 2 und deshalb k* - 1 = 1 Zählerfreiheitsgraden und n-k* Nennerfreiheitsgraden einer t-Verteilung mit n-k* Freiheitsgraden.
F0(k*) ist hier als Verhältnis der durch die jeweils zuletzt aufgenommenen unabhängigen Partial-Variable erklärten Summe der Abstandsquadrate zur nicht-erklärten Gesamtsumme der Abstandsquadrate definiert:
t(n - k*) erhalten wir bei n-k* Freiheitsgraden bei gewähltem Signifikanzniveau von Α aus der Tabelle oder über den Rechner.
Alternativ kann die Nullhypothese zurückgewiesen werden, wenn der berechnete Wert t(n - k) < 0,01 bzw. < 0,05 ist.
c) Der fallweise Test der Modellkomponenten
Der fallweise Test prüft die Signifikanz aller am Ende aufgenommen Variablen xj
Die Hypothese
wird angenommen, wenn:
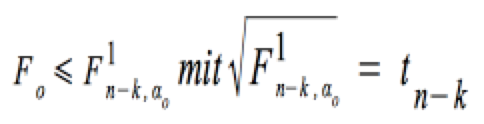
F0(k*) ist nun als Verhältnis der durch die einzelnen insgesamt aufgenommenen Variablen erklärten Gesamtsumme der Abstandsquadrate zur nicht-erklärten Gesamtsumme der Abstandsquadrate definiert:
t(n - k) erhalten wir bei n-k Freiheitsgraden bei gewähltem Signifikanzniveau von Α aus der Tabelle oder über den Rechner.
Alternativ kann die Nullhypothese zurückgewiesen werden, wenn der berechnete Wert t(n - k) < 0,01 bzw. < 0,05 ist.
3. Störfaktoren in der multiplen Regressions- und Korrelationsanalyse
Eine Beeinträchtigung der Inferenzschlüsse im Rahmen der Regressions- und Korrelationsanalyse kann durch zwei Phänomene auftreten:
Das Vorliegen derartiger Störungen kann durch die folgenden Prüfverfahren festgestellt werden.
a) Die Prüfung der Multikollinearität
b) Der Fall der Autokorrelation
Autokorrelation bezeichnet die Korrelation der Fehlervariable mit sich selbst in der Form
 .
Autokorrelation lässt sich mit den Durbin-Watson-Test feststellen.
Dabei sind für die Teststatistik "d" in Abhängigkeit von der Anzahl der Variablen (k) und der Fallzahl (n) folgende Annahme und Ablehnungsbereiche gegeben:
Abb. IV-30: Annahme- und Ablehnungsbereiche für d (bei n=100 und k=5)
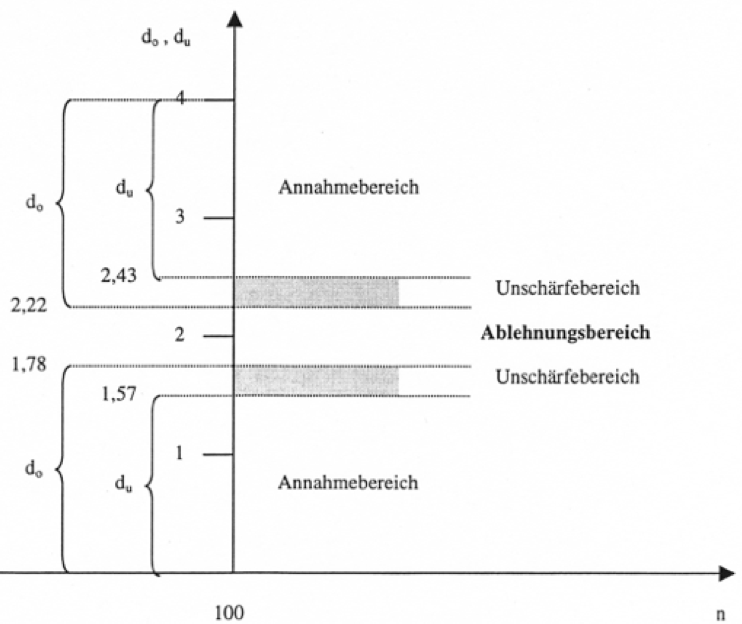
Autokorrelation kann z.B. in einer Zeitreihe gegeben sein, wenn Abweichungen von der Funktion zum Zeitpunkt t die Abweichungen zum Zeitpunkt t + 1 beeinflussen. Verfahren zur Ausschaltung der Autokorrelation (z.B. durch die Betrachtung der Differenzen zweier zeitlich aufeinanderfolgenden Werte) finden sich in der Literatur zur Zeitreihenanalyse .
Teil C (Exkurs): Die Tests der η2-Koeffizienten in der ein- und mehrfaktoriellen Varianzanalyse
Als Ergänzung zur
einfaktoriellen Varianzanalyse
und
mehrfaktoriellen Varianzanalyse in Viles 1 werden hier die Testansätze für die Komponenten des varianzanalytischen Modells vorgestellt:
Übersicht IV-1: Testansatz und -Voraussetzungen in der einfaktoriellen Varianzanalyse
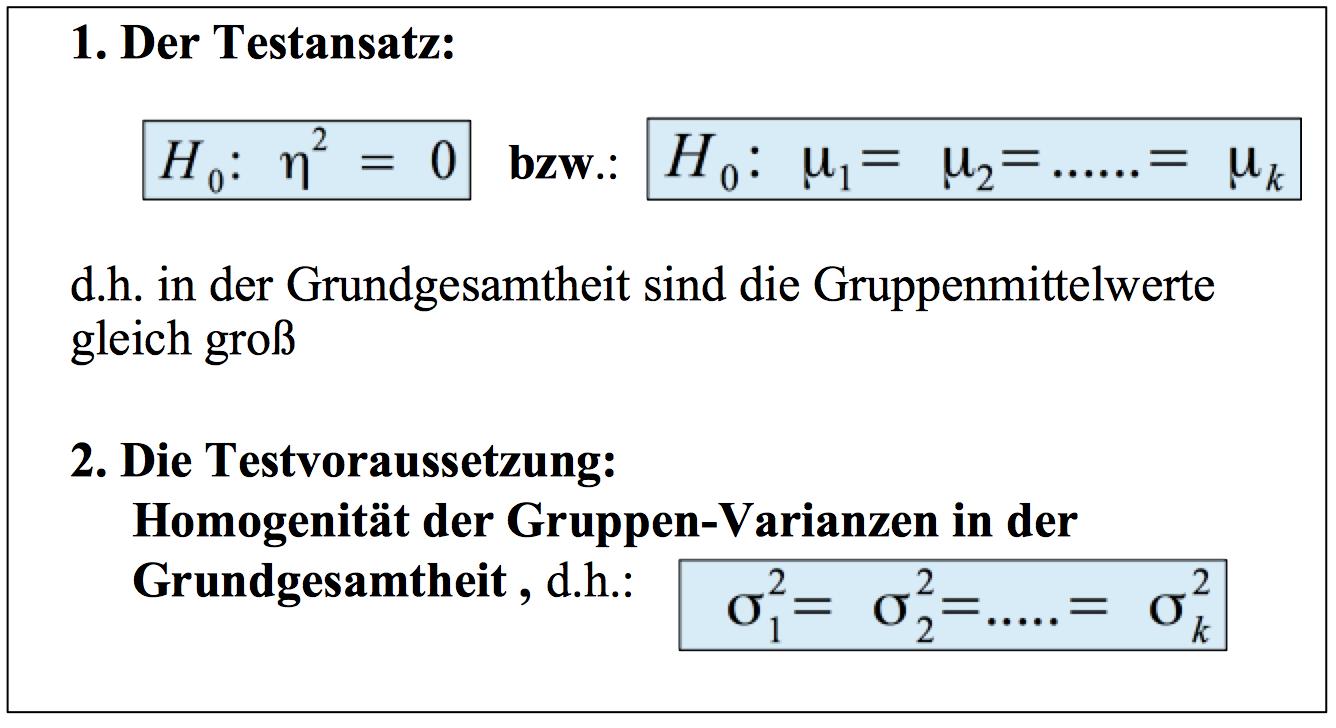
Übersicht IV-2: Die Durchführung des Tests in der einfaktoriellen Varianzanalyse
Übersicht IV-3: Test der Komponenten der mehrfaktoriellen Varianzanalyse
Hinweise:
Der Arbeitschritt "Beispiele und Aufgaben" zum Test des multiplen Regressions- und Korrelationsmodells findet sich
hier
Teil B dieses Moduls "Beispiele und Aufgaben zum Test des einfachen Regressions- und Korrelationsmodelle" findet sich unter dem Link "Nächster Text in diesem Arbeitsschritt" in der Fußleiste.
|
den multiplen Determinationskoeffizienten zwischen einer unabhängigen Variablen Xj und den übrigen unabhängigen Variablen und die "Toleranz" 
die Unabhängigkeit der Variablen Xj von den übrigen unabhängigen Variablen, dann gilt für den Standardfehler des zugehörigen partiellen Regressionskoeffizienten b*j :
), geht die
Toleranz 
gegen unendlich.
