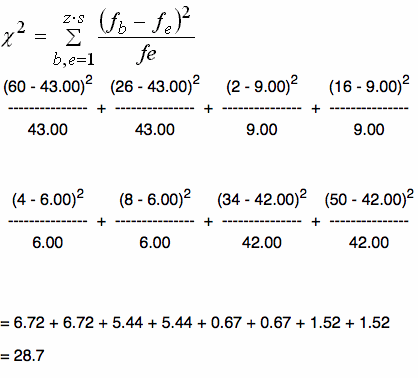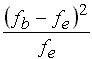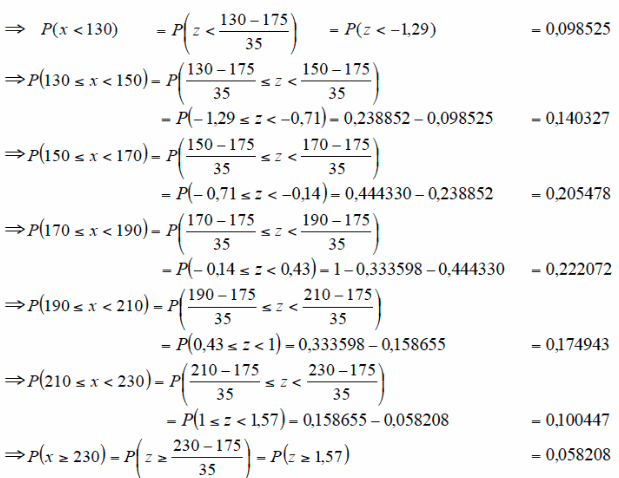| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Beispiele und Aufgaben im Modul IV-5 Chi-Quadrat-Tests
1. Beispiele und Aufgaben zum Chi-Quadrat-Unabhängigkeitstest
a) Beispiel zum Unabhängigkeitstest
Die Ausgangsdaten
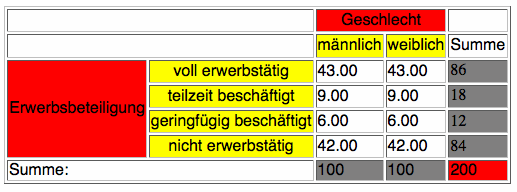
Im Modul Konzepte und Definitionen hatten wir die Wirkung des Geschlechts auf die Erwerbstätigkeit thematisiert (vgl. Tab. IV-3).
Tab. IV-3: Kontingenztabelle

Zu klären ist, ob diese Daten auf einen gesicherten Zusammenhang zwischen Geschlecht und Erwerbstätigkeit in der Grundgesamtheit schliessen lassen.
Ermittlung der bei Unabhängigkeit erwarteten Häufigkeiten fe
Eine Gegenüberstellung des Erwerbsverhalten der Geschlechter, wie es bei Unabhängigkeit der Merkmale zu erwarten wäre, liefert die Indifferenztabelle (zur Berechnung der fe vgl. das vorherige Modul).
Tab. IV-4: Indifferenztabelle
Berechnung des χ²-Wertes
Aus dem Vergleich der empirischen Werte fb der Kontingenztabelle mit den Werten der Indifferenztabelle fe ergibt sich folgende Berechnung des χ²-Wertes:
Tab. IV-5: Formel und Berechnung des χ²-Wertes
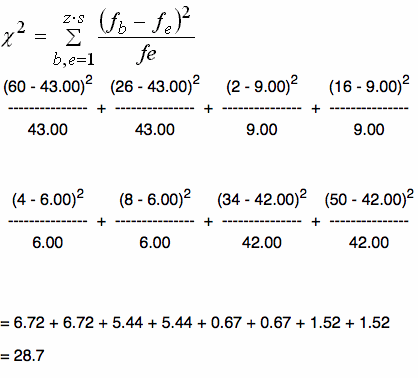
Prüfung der Voraussetzungen
Da fe ≥ 5, trifft die Annahme zu, dass der berechnete Wert χ²-verteilt ist. Damit sind die Voraussetzungen für den Test gegeben.
Bestimmung der Anzahl der Freiheitsgrade
Die Anzahl der Freiheitsgrade beträgt φ = (z - 1)(s - 1) = 3.
Testvorgaben
Wir testen die Nullhypothese H0: χ² = 0 mit einem 10%-igen Signifikanzniveau, d.h.mit α0 = 0,1.
Ermittlung des χ²0,1-Werts
Aus der Tabelle 2 der Tabellenübersicht
erhalten wir für χ²0,1 den Wert von 6,251.
Ergebnis des Tests
Der empirische Wert von 26,68 liegt deutlich über dem Grenzwert χ²α0 von 6,251.
Weil also χ² > χ²α0, kann die Hypothese der Unabhängigkeit des Erwerbsniveaus vom Geschlecht eindeutig zurückgewiesen werden.
Graphische Darstellung des Test-Ergebnisses>
Das Testergebnis wird durch die Abb.IV-19 (aus dem vorherigen Modul) bestätigt:
Abb. IV-19: Annahme- und Ablehnungsbereich
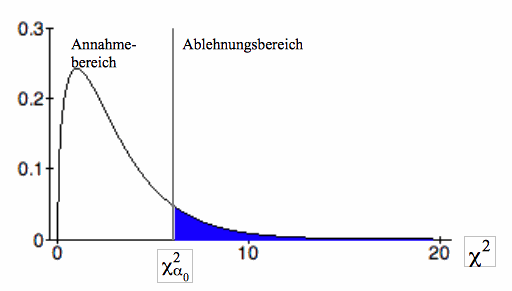
Erhöhung des Signifikanzniveaus
Wenn man das Signifikanzniveau auf 5 % erhöht, verschiebt sich die Grenze des Annahmebereichs nach rechts auf χ²0,05 = 7,815. Aber auch hier gilt: χ² > χ²α0. So dass auch bei höherer Signifikanz auf einen Zusammenhang in der Grundgesamtheit zu schliessen ist. Diese Aussage bleibt selbst bei einem Signifikanzniveau von 1 % bei χ²0,01 = 11,345 gültig.
 Mit diesem Skript können Sie die obigen Berechnungen für den Unabhängigkeitstest nachvollziehen oder die nachfolgenden Aufgaben berechnen. Aus der Tabelle 2 der
Tabellenübersicht
lassen sich die χ²α0-Werte ermitteln.
Mit diesem Skript können Sie die obigen Berechnungen für den Unabhängigkeitstest nachvollziehen oder die nachfolgenden Aufgaben berechnen. Aus der Tabelle 2 der
Tabellenübersicht
lassen sich die χ²α0-Werte ermitteln.
 Mit dem folgenden externen Tool können Sie die Grenze des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
Mit dem folgenden externen Tool können Sie die Grenze des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
b) Aufgaben zum Unabhängigkeitstest
Aufgabe 39)
Anlässlich der Fußballeuropameisterschaft möchte die Illustrierte "Neue Zeit" prüfen, ob Fußball immer noch ein reiner "Männersport" ist. Die Leserinnen und Leser sind aufgefordert in der Redaktion anzurufen und anzugeben, ob ihr Interesse "sehr groß/groß", "mittelmäßig" oder "klein/ nicht vorhanden" ist.
Nach drei Stunden hat die Praktikantin Frau Meyer 107 Anrufen entgegengenommen und erstellt folgende Tabelle:
Tab. IV-6: Interesse am Fußball nach Geschlecht
| Interesse | Frauen | Männer |
| sehr groß/groß | 18 | 25 |
| mittelmäßig | 20 | 19 |
| klein/ nicht vorhanden | 15 | 20 |
Ist das Interesse an Fußball abhängig vom Geschlecht? Testen Sie die relevante Hypothese mit einem 10%-igem Signifikanzniveau.
Bevor Sie beginnen, die Aufgabe zu lösen, nehmen Sie bitte die Resultate der Befragung in Augenschein und überlegen: Lassen die Daten eher eine Abhängigkeit des Interesses vom Geschlecht erkennen oder nicht?
 Nun können Sie obige Aufgabe
hier in 8 Schritten lösen und prüfen, ob Ihre Vermutung bezüglich des Zusammenhangs einer statistischen Prüfung Stand hält! Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Nun können Sie obige Aufgabe
hier in 8 Schritten lösen und prüfen, ob Ihre Vermutung bezüglich des Zusammenhangs einer statistischen Prüfung Stand hält! Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Aufgabe 40)
Eine Untersuchung des Zusammenhangs zwischen der Betriebsgröße (klassiert in 6 Klassen) und dem in den Betrieben erzielten Einkommen (klassiert in 9 Klassen) hat einen χ²-Wert von 61,57 erbracht. Testen Sie die Hypothese, dass es keinen Zusammenhang zwischen den beiden Variablen gibt mit einem 1 %-igen Signifikanzniveau. Die Voraussetzung für den Unabhängigkeitstest fe ≥ 5 sei erfüllt.
 Nun können Sie diese Aufgabe
hier in drei Schritten bearbeiten.
Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Nun können Sie diese Aufgabe
hier in drei Schritten bearbeiten.
Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Aufgabe 41)
Folgende Verbandsvertreter sind in den Deutschen Bundestag, 10. Wahlperiode, gewählt worden:
Tab. IV-7: Verbandsvertreter im Bundestag nach Verband und Parteizugehörigkeit
| Partei |
Arbeitnehmer- organisation |
Industrie- und Arbeitgeber- organisation |
Mittelständische Verbände |
| CDU/CSU |
19 |
15 |
44 |
| SPD |
43 |
0 |
1 |
Quelle:Bundeszentrale für politische Bildung: Informationen zur politischen Bildung, 4/87, S.16, Auszug
- Berechnen Sie als Maß für den Zusammenhang von Verbandsvertretung und Fraktionszugehörigkeit Chi- Quadrat.
- Kann aufgrund dieses Ergebnisses mit einem Signifikanzniveau von 1% behauptet werden, die Variablen seien voneinander unabhängig?
Diese Aufgabekönnen Sie
hier in sieben Schritten bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
2. Beispiele und Aufgaben zum Chi-Quadrat-Anpassungstest
a) Beispiele zum Anpassungstest
Beispiel 1:
Die Ausgangsdaten
Ein 90-faches Würfeln hat zu folgenden dargestellten absoluten Häufigkeiten geführt:
Tab. IV-8: Häufigkeit der Augenzahl beim Würfelwurf
|
Augenzahl
|
empirische Häufigkeit
|
|
1
|
19
|
|
2
|
13
|
|
3
|
14
|
|
4
|
12
|
|
5
|
17
|
|
6
|
15
|
|
Summe
|
90
|
Prüfen Sie (bei einem Signifikanzniveau von 5%), ob dieser Würfel als ideal angesehen werden kann (d.h., dass das Ergebnis gleichverteilt ist).
Ermittlung der bei Unabhängigkeit erwarteten Häufigkeiten fe
Die theoretische Verteilung ist also die Gleichverteilung. Jede Augenzahl muss die gleiche Wahrscheinlichkeit des Auftretens haben. Damit ist fe = n ·pi = 90· 1/6 = 15.
Berechnung des χ²-Wertes
Tab. IV-9: Vergleich der empirischen mit den theoretischen Häufigkeiten
|
Augenzahl
|
empirische Häufigkeit
fb
|
erwartete Häufigkeit
fe
|
fb - fe
|
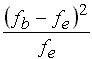
|
|
1
|
19
|
15
|
4
|
1,07
|
|
2
|
13
|
15
|
-2
|
0,27
|
|
3
|
14
|
15
|
-1
|
0,07
|
|
4
|
12
|
15
|
-3
|
0,6
|
|
5
|
17
|
15
|
2
|
0,27
|
|
6
|
15
|
15
|
0
|
0
|
|
Summe
|
90
|
90
|
|
2,2
|
Der berechnete χ²-Wert beträgt 2,2.
Prüfung der Voraussetzungen
Da fe ≥ 5, trifft die Annahme zu, dass der berechnete Wert χ²-verteilt ist. Damit sind die Voraussetzungen für den Test gegeben.
Bestimmung der Anzahl der Freiheitsgrade
Die Anzahl der Freiheitsgrade beträgt φ = k - 1 = 5.
Testvorgaben
Wir testen die Nullhypothese H0: χ² = 0 mit einem 5%-igen Signifikanzniveau, d.h.mit α0 = 0,05.
Ermittlung des χ²0,05-Werts
Aus der Tabelle 2
Tabellenübersicht
erhalten wir für χ²0,05 den Wert von 11,07.
Ergebnis des Tests
Der empirische Wert von 2,2 liegt deutlich unter dem Grenzwert χ²α0 von 11,07.
Weil also χ² < χ²α0, kann die Hypothese der Gleichverteilung angenommen werden.
Graphische Darstellung des Tests
 Ein Rechner
zur Erzeugung einer Graphik zu diesem Test findet sich wiederunter diesem externen Link
Ein Rechner
zur Erzeugung einer Graphik zu diesem Test findet sich wiederunter diesem externen Link
Beispiel 2:
Die Ausgangsdaten
Eine Erhebung unter 200 Studenten hat folgende Verteilung der Mietausgaben ergeben:
Tabelle IV-10: Verteilung der Mietausgaben oldenburger Studenten in EUR (fiktive Daten)
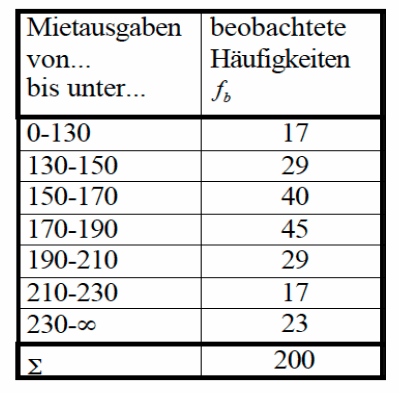
Überprüfen Sie mit einem Signifikanzniveau von 0,05 die Hypothese, dass die Mietausgaben in der Grundgesamtheit normalverteilt sind.
Ermittlung der Parameter der Normalverteilung
Die empirische Verteilung weist einen Mittelwert von 175 EUR und eine Standardabweichung von 35 EUR auf.
-
Bestimmung der Wahrscheinlichkeiten für P(X ≥ Xi) - P(X > Xi + ci)
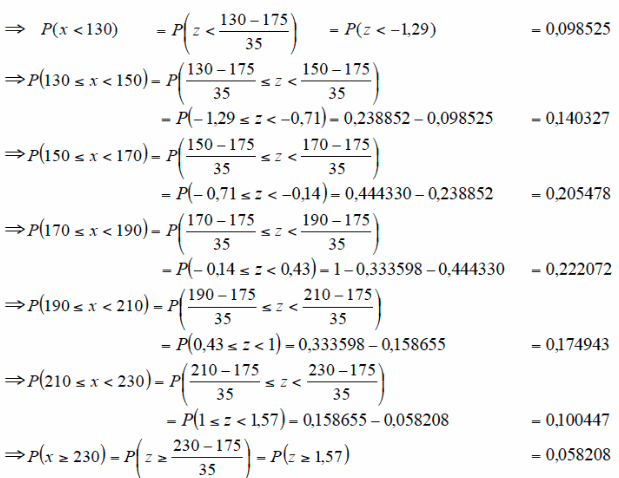
-
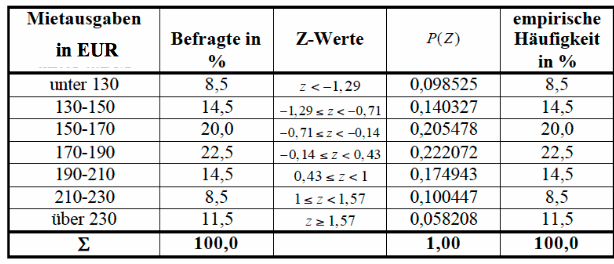
Gegenüberstellung der empirischen und normalverteilten Mietausgaben
Tabelle IV-11: empirische und normalverteilte Mietausgaben in %
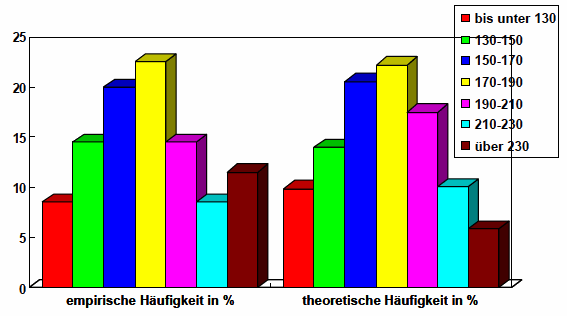
Graphischer Vergleich der Verteilungen
Abb. IV-20: empirische und normalverteilte Mietausgaben
-
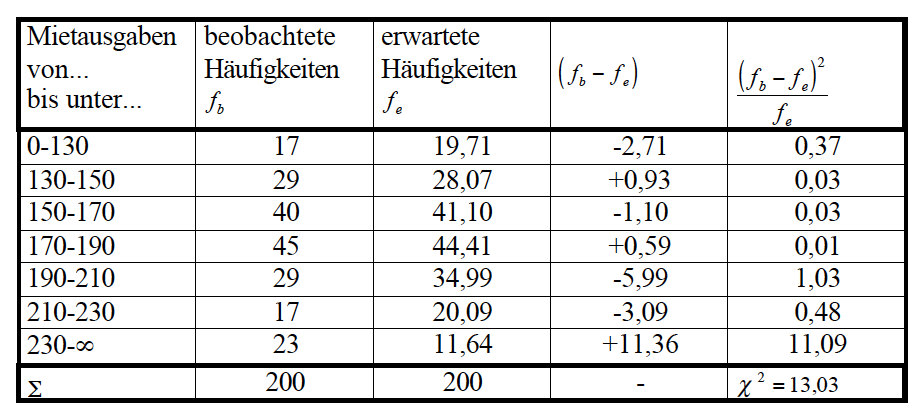
Gegenüberstellung der fb und fe und Berechnung von χ²
Tabelle IV-12: empirische und normalverteilte Häufigkeiten und Berechnung von χ²
Prüfung der Voraussetzungen
Da fe ≥ 5, trifft die Annahme zu, dass der berechnete Wert χ²-verteilt ist. Damit sind die Voraussetzungen für den Test gegeben.
Bestimmung der Anzahl der Freiheitsgrade
Die Anzahl der Freiheitsgrade beträgt φ = k - 1 = 6.
Testvorgaben
Wir testen die Nullhypothese H0: χ² = 0 mit einem 5%-igen Signifikanzniveau, d.h.mit α0 = 0,05.
Ermittlung des χ²0,05-Werts
Aus der
Tabellenübersicht
erhalten wir für χ²0,05 den Wert von 12,592.
Ergebnis des Tests
Der empirische Wert von 13,02 liegt über dem Grenzwert χ²α0 von 12,59.
Weil also χ² > χ²α0, muss die Hypothese der Gleichverteilung abgelehnt werden.
Modifikation der Testvorgaben
Bei α0 = 0,01 und φ = 6 ergibt sich für χ²0,01 ein Wert von 16,812.
Die Hypothese kann also bei einem Signifikanzniveau von 0,01 angenommen werden.
Die Festlegung des Signifikanzniveaus sollte nicht davon abhängen, ob eine Annahme oder eine Ablehnung der Hypothese erwünscht ist. Da mit einer Erhöhung des Signifikanzniveaus von 0,05 auf 0,01 der Annahmebereich ausgeweitet wird, reduziert sich zwar der α-Fehler, d.h. das Risiko eine richtige Hypothese abzulehnen, gleichzeitig steigt aber der β-Fehler, d.h.das Risiko eine falsche Hypothese anzunehmen. Aus dem Untersuchungskontext heraus wäre also abzuschätzen, welcher Fehler am problematischsten ist. Dieser sollte dann durch ein entsprechendes α0 minimiert werden.
 Mit diesem Skript können Sie Berechnungen für den Anpassungstest (auf Gleichverteilung) ausführen und z.B. die obigen Aufgaben nachrechnen bzw. die folgenden bearbeiten. Aus der Tabelle 2 der Tabellenübersicht
lassen sich die χ²α0-Werte ermitteln.
Mit diesem Skript können Sie Berechnungen für den Anpassungstest (auf Gleichverteilung) ausführen und z.B. die obigen Aufgaben nachrechnen bzw. die folgenden bearbeiten. Aus der Tabelle 2 der Tabellenübersicht
lassen sich die χ²α0-Werte ermitteln.
 Mit dem folgenden externen Tool können Sie die Grenze des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
Mit dem folgenden externen Tool können Sie die Grenze des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
b) Aufgaben zum Anpassungstest
Aufgabe 42)
Der Wintersportort "Zell am See" in Österreich wirbt in seinem Prospekt, dass in den Wintermonaten November, Dezember, Januar und Februar die Schneehöhe immer gleich ist. Herr Meyer besucht den Ort schon seit vielen Jahren und hat sehr unterschiedliche Schneehöhen vorgefunden. In einigen Jahren reichte der Schnee in den Wintermonaten nicht zum Ski fahren. Auf Grund seiner Liebe zu diesem Ort hat er sich in diesem Jahr ein kleines Haus in "Zell am See" gekauft und jeden Tag die Schneehöhe gemessen und für jeden Monat eine Durchschnittshöhe ermittelt. So liegen ihm nun folgende Daten vor:
Tab. IV-13: Schneehöhen (fiktives Beispiel)
| Monat | November | Dezember | Januar | Februar |
| Schneehöhe in cm | 66 | 59 | 71 | 68 |
Kann Herr Meyer mit diesen Daten die Angabe aus dem Prospekt widerlegen und behaupten, dass die Schneehöhe nicht gleichverteilt ist? (Signifikanzniveau 10%)
 Diese Aufgabe können Sie
hier in 8 Schritten bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Diese Aufgabe können Sie
hier in 8 Schritten bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Aufgabe 43)
Der Soziologe Max Weber stellt in dem Aufsatz "Zur Psychophysik der industriellen Arbeit" folgende Verteilung der Arbeitsunfälle männlicher Arbeiter in Kopenhagen 1898-1907 vor:
Tab. IV-14: Arbeitsunfälle nach Wochentagen
| Wochentag | Montag | Dienstag | Mittwoch | Donnerstag | Freitag | Samstag |
| Anz. der Unfälle | 50 | 46 | 34 | 34 | 33 | 43 |
Die hohe Frequenzen am Samstag und Montag hält Weber für eine Folge des Alkohols (Freitag ist Lohntag) bzw. für eine Folge größerer gesundheitlicher Strapazen am Wochenende.
a) Im Gegensatz zu Weber glauben Sie, dass die Unfälle gleichmäßig über die Wochentage verteilt sind und die Abweichungen von den erwarteten Häufigkeiten nur Zufallsschwankungen sind. Testen Sie Ihre Hypothese auf einem Signifikanzniveau von 1%. Wer hat recht? Max Weber oder Sie?
 Diese Aufgabe können Sie
hier in 8 Schritten bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Diese Aufgabe können Sie
hier in 8 Schritten bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
b) Angenommen, die Stichprobe wäre 10-mal so groß gewesen wie oben und die Verteilung sähe wie folgt aus:
Tab. IV-15: Arbeitsunfälle nach Wochentagen (fiktive Vergrößerung der Stichprobe)
| Wochentag | Montag | Dienstag | Mittwoch | Donnerstag | Freitag | Samstag |
| Anz. der Unfälle | 500 | 460 | 340 | 340 | 330 | 430 |
Testen Sie wie unter a).
c) Vergleichen Sie die unter a) und b) gefundenen Ergebnisse miteinander und kommentieren Sie diese.
 Diese Aufgabe können Sie
hier in 4 Schritten bearbeiten.
Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
Diese Aufgabe können Sie
hier in 4 Schritten bearbeiten.
Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in diesen Erläuterungen
zu berücksichtigen.
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel03_Hypothesentests/modul03_Chi-Quadrat-Tests/ebene02_Beispiele~~lund~~lAufgaben/03__03__02__01.php3