Beim Test wird vorausgesetzt, dass die Einkommen normalverteilt sind.
Die modifizierte Varianz der Stichprobe
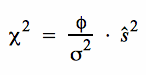
ist bei n ≤ 30 χ²-verteilt mit φ = n - 1 Freiheitsgraden.
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 2 > Kap. IV Hypothesentests > IV-4 Test der Standardabweichung und der Varianz > Beispiele und Aufgaben |
Beispiel 1:
In diesem Beispiel kommen wir auf die Frage zurück, ob die Geschäftsleitung einer Drogeriemarktkette in einem Stadtteil eine Filiale eröffnen soll. Die Neugründung sollte nun nicht nur davon abhängen, dass das für Konsumausgaben verfügbare Durchschnittseinkommen im Stadtteil 1500 EUR beträgt, sondern auch noch davon, dass die Einkommensstreuung nicht zu hoch ist.
Getestet wird darauf hin mit einem Signifikanzniveau von 5 % die Hypothese, dass die Streuung des Durchschnittseinkommens 200 EUR nicht übersteigt.
Der Jung-Betriebswirt der zuständigen Abteilung führt dazu eine weitere Umfrage unter n = 16 Personen durch. Es ergibt sich dabei eine Standardabweichung ŝ von 250 EUR.
a) Prüfung der Voraussetzungen:
Beim Test wird vorausgesetzt, dass die Einkommen normalverteilt sind.
Die modifizierte Varianz der Stichprobe
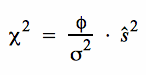
ist bei n ≤ 30 χ²-verteilt mit φ = n - 1 Freiheitsgraden.
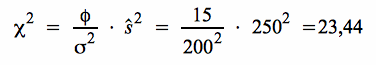
Im rechtsseitigen Test ergibt sich als Grenzwert für einen Test auf der Ebene von χ² bei einem Signifikanzniveau von 0,05 und 15 Freiheitsgraden aus der Tabelle 2 der Tabellenübersicht ein χ²-Wert von: χ²α0 = 24,996 .
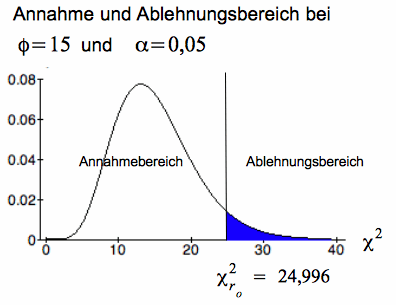
Die Grenze des Annahme- und des Ablehnungsbereichs ergibt sich graphisch in Abb. IV-18:
Abb. IV-18 Rechtsseitiger Hypothesentest
![]() Ein Rechner zur Erzeugung dieser Graphik findet sich unter diesem externen Link. Mit diesem Tool können Sie die linken und rechten Grenzen des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
Ein Rechner zur Erzeugung dieser Graphik findet sich unter diesem externen Link. Mit diesem Tool können Sie die linken und rechten Grenzen des Annahmebereichs für beliebige Chi-Quadratverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
Die Grenze des Ablehnungsbereiches ist gegeben mit:
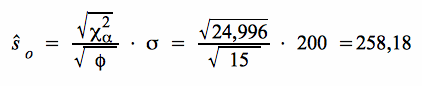 EUR.
EUR.
Das Testergebnis kann auf zwei Ebenen abgeleitet werden:
Auf der Ebene der χ²-Werte ist der Wert der modifizierten Varianz nach c) mit dem χ²α0-Wert aus d) zu vergleichen. Wie Abb. IV-18 unter e) zeigt, liegt der empirische Wert mit 23,44 unter dem Grenzwert von 24,99 und damit im Annahmebereich der Hypothese.
Entsprechend liegt die Streuung der Stichprobe mit ŝ = 250 EUR unter dem Grenzwert ŝo = 258,18 nach f) und damit ebenfalls im Annahmebereich der Hypothese.
Danach könnte die Kette die Filiale errichten.
Alternativ könnte noch die Gegenhypothese H0: σ² ≥ 200² EUR getestet werden. Erst wenn diese abgelehnt werden kann, darf die Kette sicher sein, dass σ nicht doch größer als 200 EUR ist.
Im linksseitigen Test ergibt sich als Grenzwert für einen Test auf der Ebene von χ² bei einem Signifikanzniveau von 0,05 und 15 Freiheitsgraden aus der Tabelle 2 der Tabellenübersicht ein χ²-Wert von: χ²0,95 = 7,261 .
![]() Ein Rechner zur Erzeugung der entsprechenden Graphik mit einer rechten Randwahrscheinlichkeit von 1-α = 0.95 findet sich wieder unter diesem externen Link.
Ein Rechner zur Erzeugung der entsprechenden Graphik mit einer rechten Randwahrscheinlichkeit von 1-α = 0.95 findet sich wieder unter diesem externen Link.
Auf der Eben der χ²-Werte ist der Wert der modifizierten Varianz nach c) mit dem χ²α0-Wert aus h) zu vergleichen. Dabei liegt der empirische Wert mit 23,44 über dem Grenzwert von 7,261 und damit im Annahmebereich auch der Gegen-Hypothese. Da diese Hypothese also ebenfalls nicht zurückgewiesen werden kann, resultieren aus den Tests widersprüchliche Ergebnisse. Danach sollte die Kette die Filiale besser nicht errichten.
Dem Chef-Statistiker der Marketingabteilung sind die Ergebnisse nicht nur zu widersprüchlich sondern angesichts der geringen Stichprobengröße auch zu unsicher. Er veranlasst deshalb den Jung-Betriebswirt, eine größere Stichprobe zu erheben und daran die obigen Hypothesen zu überprüfen. Diese Variante soll anhand des Beispiels 2 demonstriert werden.
Beispiel 2: Es wird nun eine Stichprobe mit n = 550 gezogen. Dabei ergibt sich eine Standardabweichung ŝ = 220 EUR. Wir führen einen Test mit einem Signifikanzniveau von 5% durch und prüfen dabei, ob die Standardabweichung der Stichprobe im Annahme- oder Ablehnungsbereich der Hypothese H0: σ ≤ 200 EUR liegt.
a) Prüfung der Voraussetzungen: Beim Test wird wieder vorausgesetzt, dass die Einkommen normalverteilt sind.
Die modifizierte Varianz der Stichprobe
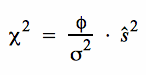
ist jetzt χ²-verteilt mit φ = n - 1 = 549 Freiheitsgraden.
Da die Tabellen für die χ²-Verteilung für n > 30 i.A. nicht vorliegen, wird diese Testvariante hier nur zu Demonstrationszwecken präsentiert.
Die Hypothese H0 lautet im rechtsseitigen Test H0: σ² ≤ 200² EUR.
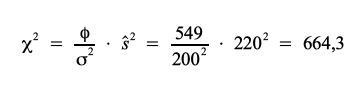
Im rechtsseitigen Test ergibt sich als Grenzwert für einen Test auf der Ebene von χ² bei einem Signifikanzniveau von 0,05 und 549 Freiheitsgraden aus dem obigen externen Tool ein Wert von: χ²α0 = 234 .
Auf der Ebene der χ²-Werte ist der Wert der modifizierten Varianz mit dem χ²α0-Wert zu vergleichen. Dabei liegt der empirische Wert mit 664,3 über dem rechten Grenzwert von 234 und damit im Ablehnungsbereich der Hypothese (vgl. dazu die Graphik aus diesem Tool).
Bei n > 30 ist eine Approximation der χ²-Verteilung durch die Standardnormalverteilung möglich.
Für n > 30 ist 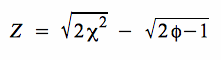 standardnormalverteilt.
standardnormalverteilt.
Dabei kann der Test, wie am Mittelwert-Test gezeigt, sowohl auf der Ebene der Z-Werte wie auf der Ebene der ŝ - Werte durchgeführt werden
Die Hypothese lautet im rechtsseitigen Test H0: Z ≤ Zα0.
(zur Ermittlung von χ² vgl. 1.2 b)
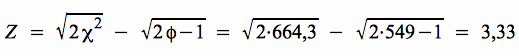
Im rechtsseitigen Test ergibt sich als Grenzwert für einen Test bei einem Signifikanzniveau von 0,05 aus der Tabellenübersicht ein Z-Wert von: Zα0 = 1,65 .
Auf der Ebene der Z-Werte ist der Z-Wert aus der Stichprobe mit dem Zα0-Wert aus der Tabelle zu vergleichen. Danach liegt der empirische Wert mit 3,33 über dem Grenzwert von 1,65 und damit schon wie unter b) im Ablehnungsbereich der Hypothese.
Die lautet nun im rechtsseitigen Test H0: σ ≤ 200 EUR.
Ermittlung des Ablehnungsbereichs
Die Grenze des Ablehnungsbereiches ist gegeben mit:
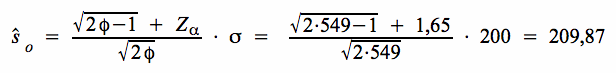 EUR.
EUR.
Entsprechend den bisherigen Ergebnissen unter b) und c-1) liegt auch hier die Streuung der Stichprobe mit ŝ = 220 EUR über dem Grenzwert ŝo = 209,87 und damit ebenfalls im Ablehnungsbereich der Hypothese.
Nach den, in 3 äquivalenten Varianten durchgerechneten Tests sollte die Kette die Filiale nicht errichten. Da diese Ergebnisse bereits über dem oberen Grenzwert liegen, erübrigt sich eine Prüfung der Gegenhypothese H0: σ² ≥ 200² EUR. Diese wäre auf jeden Fall dann anzunehmen.
Hinweis: Bestimmen Sie je nach Aufgabenstellung den unteren und/oder oberen Grenzwert des Annahmebereichs der jeweiligen Hypothese. Setzen Sie dazu die passenden Werte in die Felder der Formeln ein. Nicht benötigte Felder lassen Sie unverändert.