Die Ausgangsdaten
Die Kompetenz einer Partei im Bereich „Allgemeine Sicherheit“ wurde in der Vergangenheit auf einer Skala von 0 – 10 durchschnittlich mit 6,7 Punkten bewertet. Nach einer kontroversen Parlamentsdebatte soll die Hypothese getestet werden, die Glaubwürdigkeit der Partei sei danach unverändert, wenn nicht sogar gestiegen. In einer Blitzumfrage mit n = 100 ergibt sich ein durchschnittlicher Punktewert von 6,35 bei einer Standardabweichung ŝ von 1,2 Punkten.
Die Testvorgaben
Mit Hilfe des Hypothesen-Tests soll nun überprüft werden, ob sich die durchschnittliche Glaubwürdigkeit wirklich erhöht oder nicht doch verringert hat. Die möglichen Hypothesen lauten:
H0: μ ≥ μ0 (die Glaubwürdigkeit ist jetzt gleich oder größer)
H0: μ < μ0 (die Glaubwürdigkeit ist jetzt geringer)
Die Partei entscheidet sich dafür, die optimistische Hypothese mit einem Signifikanzniveau α0 von 5 % zu testen.
Prüfung der Voraussetzungen
Auf den Endlichkeitsfaktor können wir bei dieser Aufgabe verzichten.
Ermittlung des (Zα0)-Werts
Zur Durchführung des Tests benötigen wir den Z-Wert (Zα0), der sich für das gewählte α0 = 0,05 ergibt. Aus der Tabelle erhalten wir: (Zα0) = -1,65.
Durchführung des Tests
Wir führen den Test nun beispielhaft in drei äquivalenten Varianten durch:
Vergleich der Z-Werte
Mit Hilfe der Z-Transformation berechnen wir den Z-Wert, der sich aus den Angaben ergibt:
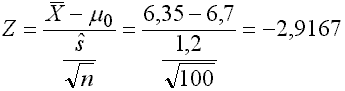
Der empirische Z-Wert liegt, wie die linke Seite der Abbildung IV-5 zeigt, im Ablehnungsbereich.
Vergleich der X̄-Werte
Rechnet man die Aufgabe mit der nach X̄ aufgelösten Z-Transformationsformel, erhält man:
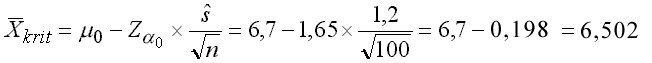
Hier liegt nun das empirische X̄ im Ablehnungsbereich (vgl. rechte Seite der Abb. IV-5).
Abb. IV-5 Annahme- und Ablehnungsbereiche für Z und für X̄
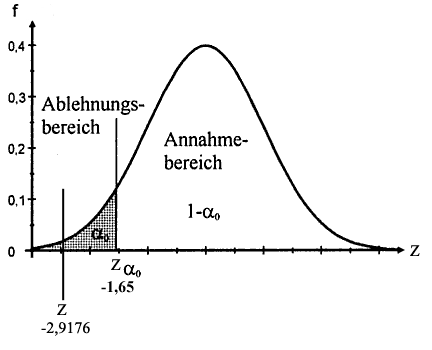
P( Z ≤ - 1,65) = 0,05 |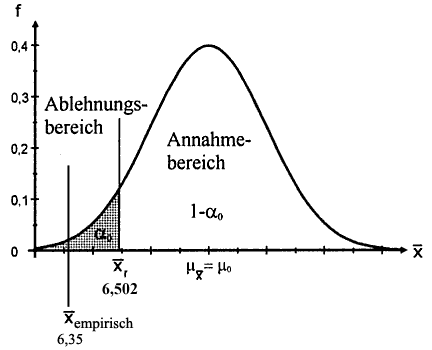 
P( X̄ ≤ 6,502) = 0,05 |
Vergleich der α-Werte
Alternativ zu den beiden Rechnungen unter 1. und 2. können wir für den unter 1. errechneten empirischen Z-Wert von -2,9167 in der Tabelle das ihm entsprechende empirische α ermitteln und mit α0 vergleichen. Dem Z-Wert von -2,9167 entspricht ein α von 0,00175. Dieser Wert ist wesentlich kleiner als 0,05, was ebenfalls zur Ablehnung der Hypothese führt (vgl. dazu Abb. IV-5 linke Graphik).
Ergebnis des Tests
Nach allen Rechnungsvarianten muss also die H0 zugunsten der H1 verworfen werden, Somit kann behauptet werden, dass sich die Glaubwürdigkeit mit einer Signifikanz von 5% verringert hat.
Modifikation der Testvorgaben
Hätte die Partei nicht die optimistische Hypothese sondern die Gegenhypothese getestet, wäre es bei obigen Stichprobenwerten natürlich zu einer eindeutigen Zustimmung zur pessimistischen Varianten gekommen.
Graphische und rechnerische Demonstration von Annahme-/Ablehnungsbereichen
Mit dem folgenden externen Tool können Sie die Grenzen des Annahmebereichs für beliebige Normalverteilungen mit selbst gewähltem Signifikanzniveau berechnen und graphisch darstellen lassen.
