In Symbolen schreibt man:
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 2 > Kap. IV Hypothesentests > IV-1 Allgemeine Aspekte des Testmodells > Konzepte und Definitionen |
Wie ausgeführt, stellt eine Stichprobenverteilung die Grundlage eines Hypothesentests dar.
Allerdings beruht die Verteilung nicht auf den tatsächlichen Parametern der Grundgesamtheit sondern auf angenommenen. Der Test basiert also auf einer hypothetischen Stichprobenverteilung.
Liegt nun die Stichprobenstatistik (z. B. deren Mittelwert) im Zentrum dieser hypothetischen Stichprobenverteilung, gibt es keine Veranlassung, die Hypothese in Zweifel zu ziehen. Fällt die Statistik jedoch in deren Randbereiche, ist es sinnvoller anzunehmen, die Hypothese sei falsch, als zu unterstellen, die Hypothese sei richtig und die Stichprobe leider ein Ausreisser.
Insgesamt sind bei der Durchführung eines Tests folgende Schritte zu unternehmen:
Festlegung des Wertebereichs der Stichprobenstatistik, der zur Annahme bzw. Ablehnung der Hypothese führt,
Spezifizierung der Signifikanz des Testergebnisses
Abklärung der Testrisiken,
Berechnung der Grenzen des Annahmebereichs,
Bestimmung des Stichprobenumfangs,
Erhebung der Stichprobe und Entscheidung über Annahme oder Ablehnung der Hypothese.
Beim Hypothesentest werden zwei Arten von Hypothesen unterschieden: Die Punkt- und die Bereichshypothese.
Wird eine Hypothese (H) als Punkthypothese formuliert, überprüft
der Test die Glaubwürdigkeit genau eines Wertes, nämlich
des festgelegten. Die Hypothese "Das durchschnittliche
Bruttoeinkommen in dem Ort A beträgt 3800 EUR pro Haushalt"
kann nur dann angenommen werden, wenn der gefundene Mittelwert aus der
Stichprobe sich nicht signifikant von 3800 unterscheidet.
In Symbolen schreibt man:
![]() .
.
Stellen wir uns vor, dass die Untersuchung von einer Drogeriekette durchgeführt wird, die prüfen möchte, ob die potentiellen Kunden für eine Geschäftsansiedlung ausreichend betucht sind. In diesem Falle wäre die Geschäftsleitung sicherlich auch zu einem Bau bereit, wenn das mittlere Bruttoeinkommen über den geforderten 3800 EUR liegt. Dieses Beispiel zeigt, dass Punkthypothesen gerade in den Wirtschafts- und Sozialwissenschaften oft nicht so geeignet sind wie Bereichshypothesen.
Eine Bereichshypothese umfasst deshalb
nicht nur einen bestimmten Wert, sondern einen Bereich einschließlich
eines Wertes bis ± ∞ , deshalb müssen wir zwei Arten von Bereichshypothesen unterscheiden:
H0: μ ≥ μ0 und H0: μ ≤ μ0 .
Oft bietet es sich bei Bereichshypothesen an, nicht die vordergründig erwünschte Hypothese auf Annahme (hier am Beispiele der Drogeriekette: H0: μ ≥ 3800 EUR), sondern die unerwünschte Hypothese (hier: H0: μ ≤ 3800 EUR) auf Ablehnung zu testen. I.A. wird die letztlich getestete Hypothese als H0 und die Alternativhypothese als H1 bezeichnet.
Eine Hypothese H0 kann nach einem Test entweder
angenommen oder abgelehnt werden. Die Frage, wann eine Hypothese
abgelehnt und wann angenommen wird, hängt davon ab, wie weit der
hypothetische Wert der Grundgesamtheit und der ermittelte Wert der
Stichprobe auseinanderklaffen dürfen, ohne dass von einem
signifikanten Unterschied gesprochen werden muss.
Fällt nun der Wert aus der Stichprobe in den
Ablehnungsbereich, wird die H0 abgelehnt. Wo der
Ablehnungs- bzw. der Annahmebereich liegt, entscheidet die Formulierung der Hypothese.
Wird ein beidseitiger Test durchgeführt mit der Punkt-Hypothese: H0: μ = μ0
führen zu kleine und zu große Werte
zum Ablehnen der H0.
Die folgende Graphik zeigt den
Annahme- und Ablehnungsbereich:
Abb. IV-1 beidseitiger Test H0: μ = μ0 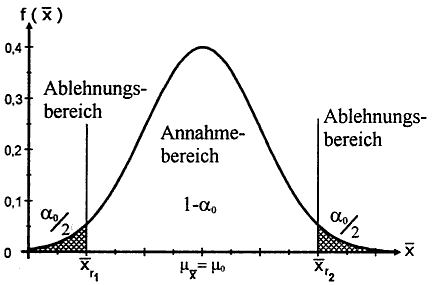
P( X̄ ru ≤ X̄ ≤ X̄ ro) = 1 - α0
Im Fall der Bereichs-Hypothese:
H0: μ ≤ μ0
liegt ein rechtsseitiger Test vor, bei dem die Hypothese nur abgelehnt werden kann, wenn der Mittelwert der Stichprobe am rechten Rand der Stichprobenverteilung liegt.
Im Fall der Bereichs-Hypothese:
H0: μ ≥ μ0
ist ein linksseitiger Test gegeben, bei dem ein Stichprobenmittelwert am linken Rand der Stichprobenverteilung zur Ablehnung der Hypothese führt.
D.h. bei einem rechtsseitigen Test führen zu große Werte zum
Ablehnen der H0, bei einem linksseitigen Test zu kleine
Werte zum Ablehnen.
Die folgenden Graphiken zeigen die
Annahme- und Ablehnungsbereiche für die beiden
Testansätze:
|
Abb. IV-2 linksseitiger Test
H0: μ ≥ μ0 |
rechtsseitiger Test H0: μ ≤ μ0 | ||
In allen drei Fällen ist die Wahrscheinlichkeit α0, die Hypothese abzulehnen, (d.h. die Größe der schraffierten Randfläche/n) gleich groß. Im Falle des beidseitigen Tests wird sie nur auf einen rechten und einen linken Randbereich aufgeteilt.
Bevor ein Test
durchgeführt wird, muss ein entsprechendes Signifikanzniveau
gewählt werden, das mit α0
gekennzeichnet wird. Es bestimmt die Größe des Bereichs, in dem die H0
abgelehnt wird, d.h die Größe der schraffierten Fläche in den Abb. IV-1 u. IV-2.
Bei einseitigen Tests liegt der Ablehnungsbereich mit der Größe α0 entweder auf der linken oder der rechten Seite der Verteilung. Bei einem beidseitigen Test teilt sich die Größe α0 in zwei gleich große Bereiche α0/2 auf.
Das konkrete Signifikanzniveau α0
muss vor jedem Test individuell gewählt werden. In den
Wirtschafts- und Sozialwissenschaften liegen typische Werte bei 0,1; 0,05 oder 0,01, d.h. bei 10%,
5% oder 1%. Diese Größe bestimmt sowohl wie groß der
Ablehnungsbereich als auch wie groß der Annahmebereich der
Hypothese (1 - α0) ist.
Das Wählen des Signifikanzniveaus ist immer eine
"Gradwanderung". Je größer der Wert, desto
größer der Ablehnungsbereich, desto größer die
Chance, die H0 zugunsten der H1 zu verwerfen.
Jedoch sinkt damit gleichzeitig die sog. Signifikanz des Ergebnis.
Unter der Voraussetzung, dass die eigentlich unerwünschte
Hypothese auf Ablehnung getestet werden sollte (und nur unter dieser
Voraussetzung macht der Begriff einer hohen Signifikanz einen
positiven Sinn), erschwert ein kleiner α0-Wert
die Ablehnung der unerwünschten Hypothese. Fällt das
Stichprobenergebnis dennoch in den Ablehnungsbereich, kann man mit
einer hohen Signifikanz von der Richtigkeit der erwünschten
Hypothese ausgehen.
Wären die Folgen einer unerwünschten
Hypothese sehr gravierend, empfiehlt es sich mit noch kleinerem
Signifikanzniveau als 1% zu testen. In explorativen Untersuchungen
kann aber auch gerade am Anfang des Forschungsprozesses auch ein
Niveau von 10% gewählt werden.
Fällt das Stichprobenergebnis in den Ablehnungsbereich, heißt das noch nicht notwendigerweise, dass die abgelehnte Hypothese falsch ist. Da mit der Wahrscheinlichkeit von α0 ein Stichprobenwert auch bei richtiger Hypothese in den Ablehnungsbereich fällt, begehen wir in diesem Fall den Fehler, die richtige Hypothese abzulehnen. Dieser Fehler wird deshalb α-Fehler genannt.
Fällt das Stichprobenergebnis andererseits in den
Annahmebereich, muss das noch nicht bedeuten, dass der hypothetische
Wert der Grundgesamtheit der "Realität" entspricht. Es
kann durchaus passieren, dass man sich dann für eine "falsche"
Hypothese entscheidet. Diese Tatsache bezeichnet man als β-Fehler.
Zu bedenken ist, dass der β-Fehler umso kleiner wird, je mehr sich der tatsächliche und der hypothetische Wert unterscheiden. Zudem kann er durch eine Erhöhung des Stichprobenumfangs verkleinert werden. In der Praxis hängt die Notwendigkeit seiner Reduktion davon ab, welche Kosten mit einem α- bzw. β-Fehler verbunden sind.
Wir unterscheiden somit zwei Fehlerarten: α- und β- Fehler. Dieser Sachverhalt ist nochmals in der folgenden Tabelle dargestellt:
Tab. IV-1 Fehlertabelle beim Hypothesentest
|
ja |
nein |
||
|
Stichprobe fällt in den Annahmebereich |
ja |
||
Der β-Fehler kann nur bestimmt werden, wenn der tatsächliche Wert des zu testenden Parameters bekannt ist. Für alternative "Realitäten" lässt er sich abschätzen.
In der folgenden Abb. IV-3 ist die Stichprobenverteilung der X̄ auf der Basis der Hypothese H0: μ = μ0 dargestellt. Bei gegebenem Signifikanzniveau wird diese Hypothese angenommen, wenn X̄ u ≤ X̄ ≤ X̄ o .
Wenn nun aber nicht H0: μ = μ0 die richtige Hypothese ist sondern H1: μ = μ1, gibt β die Wahrscheinlichkeit an, dass der Stichproben-Mittelwert in den Bereich X̄ u ≤ X̄ ≤ X̄o fällt.
Somit ist β = P ( X̄ u ≤ X̄ ≤ X̄o | μ1).
(zu den genaueren Modalitäten vgl. die Lehrbuchliteratur, z.B. Litz 2003, S. 354 ff).
Abb. IV-3 Abschätzung des β-Fehlers
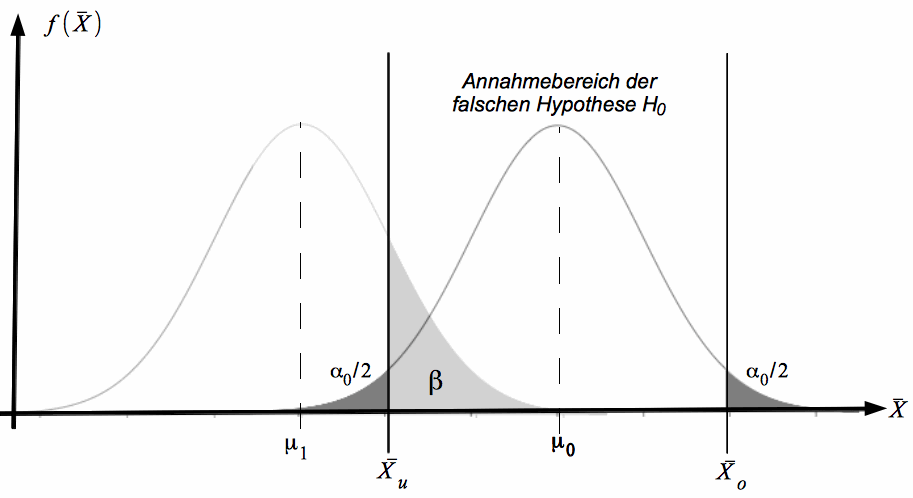
α- und β-Fehler korrespondieren somit: Je kleiner der α- desto größer ist der β-Fehler. Dies ist die Folge einer mit der Minimierung des α-Fehlers einher gehenden Vergrößerung des Annahmebereichs. Damit nimmt natürlich die Wahrscheinlichkeit zu, eine falsche Hypothese anzunehmen.
Sind die Hypothesen aufgestellt und das Signifikanzniveau gewählt, muss noch bestimmt werden, wo die Grenzwerte des Annahme- bzw. Ablehnungsbereiches (auch kritische Werte oder Rückweisungspunkte) exakt liegt. Die Lokalisierung der kritischen Grenze kann auf drei, bezüglich des Testergebnisses identische Arten erfolgen.
Am einfachsten vergleicht man den/die - aus der Tabelle bei
gegebenem α0 nachgeschlagenen
- kritischen Wert(e) Z α bzw. Z α/2 (d.h. den entsprechenden Werte in
dieser Übersicht)
mit
dem Wert der Z-Transformation (wenn σ nicht bekannt ist, was die Regel ist, wird es durch ŝ
geschätzt, vgl. die nächsten Module):
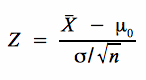
Für eine Hypothese H0: μ ≤ μ0 zeigt die nachfolgende Graphik bei einem Signifikanzniveau von α = 0,05 den Annahme- und Ablehnungsbereich der Hypothese:
Abb. IV-4 rechtsseitiger Test bei α = 0,05
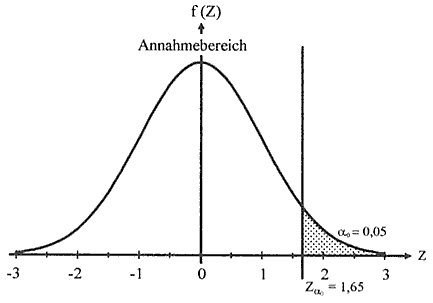
P( Z ≥ Z α) = α0
Der Ablehnungsbereich (hier für einen rechtsseitigen Test) ist dabei schraffiert. Wenn der aus der Z-Transformation bestimmte Z-Wert in diesen Bereich fällt, d.h. wenn Z > Z α wird die Hypothese abgelehnt.
Im zweiten (analogen) Fall kann die Z-Formel nach dem kritischen X̄-Wert
aufgelöst werden, so dass man folgende Bereichsgrenzen erhält:
für den
beidseitigen Test:
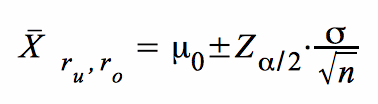
für
den rechtsseitigen Test:
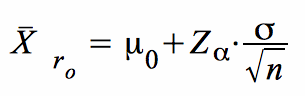 und
und
für
den linksseitigen Test:
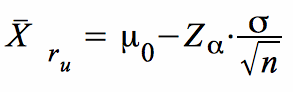
Die kritischen Werte sind graphisch in den Abbildung IV-1 - IV-3 dargestellt.
Dieser zweite Weg hat gegenüber dem ersten den Vorteil, dass er erkennbar macht, wie groß die Abweichung zwischen dem gefundenen Stichprobenwert X̄ und dem, noch die Hypothese stützenden X̄r-Wert ist.
Im dritten (ebenfalls analogen) Fall wird der, dem Z-Wert aus der Transformationsformel 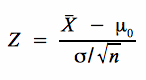 zuzuordnende α-Wert mit dem gewählten Signifikanzniveau α0 verglichen. Ein Wert von α, der im beidseitigen Test kleiner als α0/2, im links- und rechtsseitigen Test kleiner als α0 ist, führt dann ebenfalls zur Ablehnung der Hypothese. Diese Vorgehensweise findet sich z.B. bei Hypothesentests im Rahmen von SPSS.
zuzuordnende α-Wert mit dem gewählten Signifikanzniveau α0 verglichen. Ein Wert von α, der im beidseitigen Test kleiner als α0/2, im links- und rechtsseitigen Test kleiner als α0 ist, führt dann ebenfalls zur Ablehnung der Hypothese. Diese Vorgehensweise findet sich z.B. bei Hypothesentests im Rahmen von SPSS.
Aus den Formeln in 5.b ergibt sich die Erkenntnis, dass die Breite des Annahmebereichs wesentlich vom Stichprobenumfang n mit bestimmt wird. Damit hat es die testende Institution selbst in der Hand, durch Vergrößerung des Stichprobenumfangs die Gefahr zu vermindern, eine falsche Hypothese anzunehmen, d. h. einen β-Fehler zu begehen.
Gerät dabei der Stichprobenumfang über die 10%-Grenze, ist bei den Berechnungen der Endlichkeitsfaktor zu berücksichtigen.
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel03_Hypothesentests/modul01_Allgemeine~~lAspekte~~ldes~~lTestmodells/ebene01_Konzepte~~lund~~lDefinitionen/03
__01__01__01.php3