Geht man von einer Summenvariable
![]() aus,
wobei Xi normalverteilt ist,
dann sind die
aus,
wobei Xi normalverteilt ist,
dann sind die
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 2 > Kap. III Stichprobenverteilungen > III-1 Stichprobenverteilungen des arithmetischen Mittels > Konzepte und Definitionen |
Aus einer normalverteilten
Grundgesamtheit ergibt
sich die Verteilung der Mittelwerte von
Stichproben theoretisch aus der Reproduktionseigenschaft
der Normalverteilung.
Danach sind Linearkombinationen einer oder
mehrerer unabhängiger, normalverteilter Zufallsvariablen wieder
normalverteilt.
Betrachtet man die einzelnen Elemente der Stichprobe
jeweils als unabhängige normalverteilte Zufallsvariable, so gilt
die Reproduktionseigenschaft sowohl bezüglich ihrer Summe wie
ihres arithmetischen Mittels:
Geht man von einer Summenvariable
![]() aus,
wobei Xi normalverteilt ist,
dann sind die
aus,
wobei Xi normalverteilt ist,
dann sind die
Stichprobenmittelwerte![]() ebenfalls
normalverteilt mit dem
ebenfalls
normalverteilt mit dem
Erwartungswert: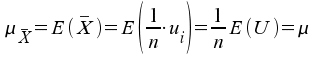 und der
und der
Varianz: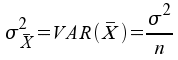 sowie
der
sowie
der
Standardabweichung: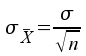 .
.
Diese wird auch als Standardfehler des arithmetischen Mittels bezeichnet.
Das Ergebnis für
die Varianz folgt aus: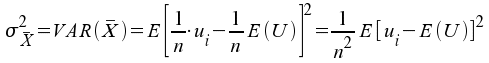 bei
bei![]() .
.
Abbildung III-4: Vergleich der Verteilung der x in der Grundgesamtheit mit der Verteilung der X̄ der Stichprobe
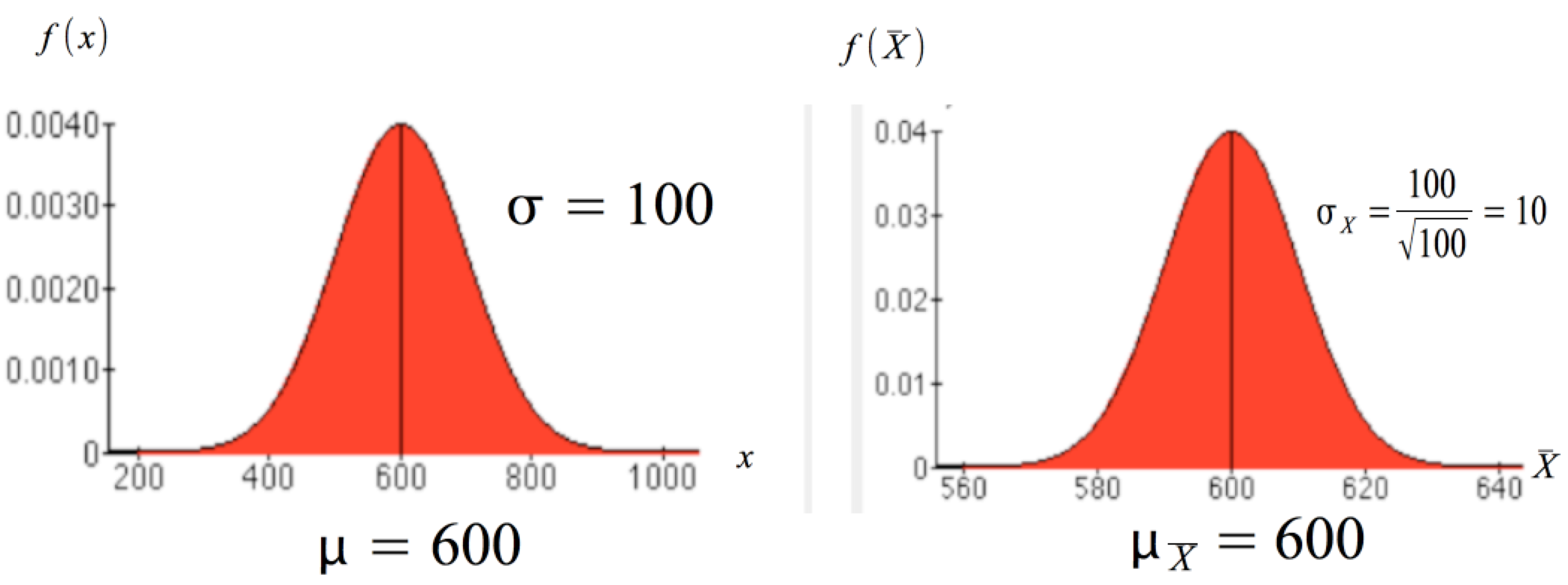
Beim Vergleich der Verteilungen ist die unterschiedliche Skalierung beider Achsen zu beachten. Für die Grundgesamtheit gilt:
0 ≤ f(x) ≤ 0,004 und 200 ≤ x ≤1000, während in den zentralen Bereich der Verteilung der X̄ gilt:
0 ≤ f(X̄) ≤ 0,04 und 570 ≤ X̄ ≤ 630.
Nach dem zentralen Grenzwertsatz
gilt nun, dass auch das arithmetischen Mittel von unabhängigen
Zufallsstichproben aus nicht-normalverteilten Grundgesamtheiten
ab![]() normalverteilt
ist.
normalverteilt
ist.
Die
Unabhängigkeit der Stichprobenelemente
ist theoretisch nur gegeben bei Zurücklegen der Elemente. Wenn
die Stichprobe mehr als 5% der Grundgesamtheit beinhaltet, der
Auswahlsatz also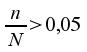 ist,
muss bei der Bestimmung der Varianz ein so genannter
Endlichkeitsfaktor
ist,
muss bei der Bestimmung der Varianz ein so genannter
Endlichkeitsfaktor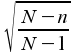 berücksichtigt
werden.
berücksichtigt
werden.
Es gilt dann für größere Stichproben:
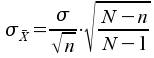
Ist![]() normalverteilt,
resultiert aus der Z-Transformation
die Standardnormalvariable
normalverteilt,
resultiert aus der Z-Transformation
die Standardnormalvariable
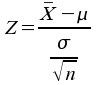 bzw.
bei
bzw.
bei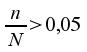 :
:
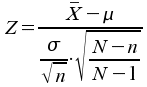
Beim Ziehen von
Stichproben ist es wünschenswert, dass die Ergebnisse nicht zu
weit vom entsprechenden Parameter der Grundgesamtheit entfernt sind.
Die Grenzen eines akzeptablen, symmetrischen
Bereichs um![]() werden
mit
werden
mit![]() bezeichnet.
Für eine vorgegebene (Ausschuss-)Wahrscheinlichkeit
bezeichnet.
Für eine vorgegebene (Ausschuss-)Wahrscheinlichkeit![]() liegen
die Stichprobenmittelwerte im Intervall:
liegen
die Stichprobenmittelwerte im Intervall:
![]() .
.
Wird die
Formel für die obige Z-Transformation
nach![]() aufgelöst,
können die Grenzen konkret bestimmt werden mit:
aufgelöst,
können die Grenzen konkret bestimmt werden mit:
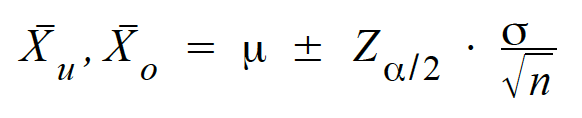
U.U. ist zusätzlich der Endlichkeitsfaktor zu berücksichtigen.
In
der Regel ist die Standardabweichung der Grundgesamtheit nicht
bekannt. Man schätzt![]() dann
durch die Standardabweichung der Stichprobe. Im Gegensatz zum
Stichprobenmittelwert
dann
durch die Standardabweichung der Stichprobe. Im Gegensatz zum
Stichprobenmittelwert![]() ist
die Stichprobenvarianz
ist
die Stichprobenvarianz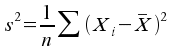 nicht
erwartungstreu, d.h.
nicht
erwartungstreu, d.h.
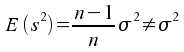 .
Auf die ausführliche Herleitung kann an dieser Stelle verzichtet
werden.1
.
Auf die ausführliche Herleitung kann an dieser Stelle verzichtet
werden.1
Ein
erwartungstreuer Schätzer für die Varianz der
Grundgesamtheit wäre erforderlich, um die Verteilung
des Stichprobenmittelwerte auch dann bestimmen zu können, wenn
die Varianz der Grundgesamtheit unbekannt ist. Zur Lösung dieser
Problematik ist es notwendig, das Konzept der Stichprobenvarianz
zu modifizieren. Der gesuchte
modifizierte Parameter, dessen Erwartungswert gleich der Varianz der
Grundgesamtheit ist, wird als modifizierte Stichprobenvarianz
bezeichnet und mit dem Symbol![]() (gelesen
„s Dach“)
gekennzeichnet.
(gelesen
„s Dach“)
gekennzeichnet.
Definiert ist die modifizierte Stichprobenvarianz als:
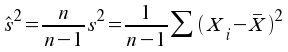
Es lässt sich leicht zeigen, dass diese modifizierte Stichprobenvarianz tatsächlich ein erwartungstreuer Schätzer für die Varianz der Grundgesamtheit ist:
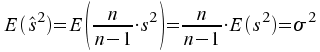
Wird![]() durch
durch![]() ersetzt,
folgt die Verteilung der Stichprobenmittelwerte keiner
Normalverteilung sondern einer t-Verteilung.
ersetzt,
folgt die Verteilung der Stichprobenmittelwerte keiner
Normalverteilung sondern einer t-Verteilung.
In diesem Fall gilt:

ist
t-verteilt mit
![]() Freiheitsgraden.
Freiheitsgraden.
Ihre Parameter sind E(t) = 0 und VAR(t) = φ/(φ-2).
Abbildung III-5: t-Verteilung der X̄ bei n = 10
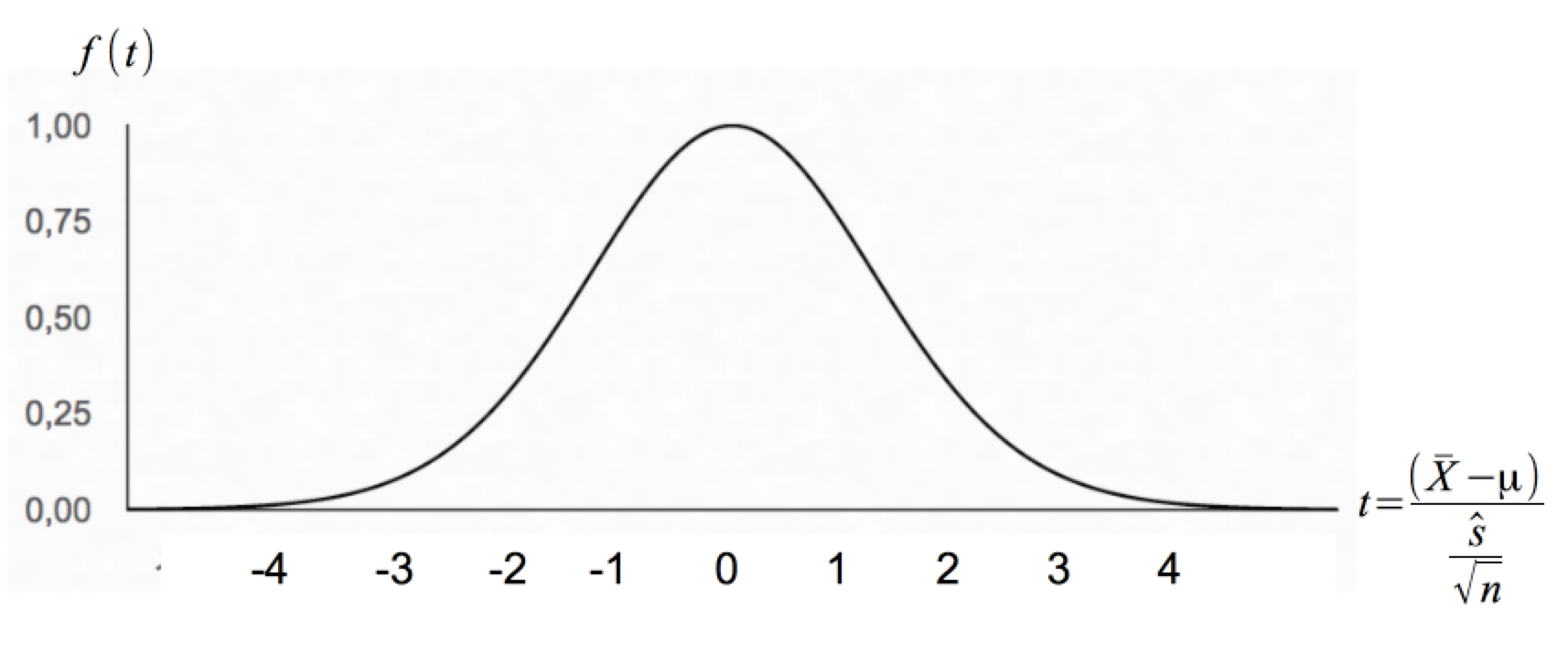
Bei
![]() ist
der Endlichkeitsfaktors zu berücksichtigen:
ist
der Endlichkeitsfaktors zu berücksichtigen:
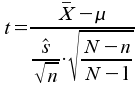
Für Stichproben mit![]() wird
die t-Verteilung durch die die Standardnormalverteilung
approximiert.
wird
die t-Verteilung durch die die Standardnormalverteilung
approximiert.
Somit gilt dann:
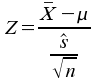 bzw.
bzw.
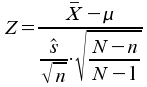
sind standardnormalverteilt.
1vgl. dazu Litz 2003, S.316 f.
letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel02x5_Stichprobenverteilungen/modul01_Stichprobenverteilungen~~ldes~~larithmetischen~~lMittels/ebene01_Konzep
te~~lund~~lDefinitionen/02x5__01__01__01.php3