III Stichprobenverteilungen

ViLeS 2 > III Stichprobenverteilungen

III Stichprobenverteilungen

- Einleitung und Modulübersicht -

1. Vorbemerkungen

Stichprobenverteilungen sind Verteilungen von Stichprobenstatistiken. Sie existieren nicht real sondern nur als theoretische Modelle, die uns angeben, mit welchen Wahrscheinlichkeiten bzw. W-Dichten die einzelnen Realisationen von Stichprobenstatistiken (Mittelwerte, Standardabweichungen, Anteilswerte) zu erwarten sind.
Als empirische Verteilungen ergäben sie sich nur, wenn alle denkbarenunterschiedlichen Stichproben auch tatsächlich gezogen und ausgewertet würden.
Die folgende Abbildung soll einen ersten Überblick über diese Zusammenhänge als Voraussetzungen des statistischen Induktionsschlusses geben:

Abbildung III-1: Zur Logik der Stichprobenverteilungen

2. Die Stichprobenverteilungen als Brücke zwischen Grundgesamtheit und Stichprobe

a) Die Parameter der Grundgesamtheit, der Stichprobe und der Stichprobenverteilungen

Angesichts der unterschiedlichen Betrachtungsebenen ist es notwendig, klar zu unterscheiden, ob von Parametern der Grundgesamtheit, den Parametern einer einzelnen Stichprobe oder den Parametern der Stichprobenverteilung gesprochen wird.

Zur Unterscheidung der Parameter der Grundgesamtheit und der Parameter der Stichprobe bedienen wir uns der folgenden Schreibweisen:

Übersicht III-1: Parameter der Grundgesamtheit und Parameter der Stichprobe

Grundgesamtheit	Parameter	Stichprobe
	Mittelwert
	Standardabweichung	bzw.
	Anteilswert
	Umfang

Wie in der folgenden Übersicht III - 2 zu sehen ist, kommen für die betrachteten Stichprobenverteilungen der,undjeweils eigene Verteilungsparameter (deren Erwartungswerte und Varianzen) hinzu, die wiederum von den, in Tabelle III – 1 enthaltenen, zu unterscheiden sind.

Übersicht III - 2: Parameter der Stichprobenverteilungen

b) Die Funktion der Stichprobenverteilungen

Die Stichprobenverteilungen stellen die Brücke dar zwischen der einzelnen gezogenen Stichprobe und der Grundgesamtheit, aus der diese gezogen wurde. Sie erlauben die Einschätzung, wie eine konkret gezogene Stichprobe zu beurteilen ist.
Für Schlüsse von einer Stichprobe auf die Grundgesamtheit (in der Regel von einem Parameter der Stichprobe auf den entsprechenden Parameter der Grundgesamtheit) ist es natürlich höchst bedeutsam, wo die Zentren der Stichprobenverteilungen liegen und wieweit die Stichprobenstatistiken um diese Zentren streuen.
Letztlich lässt sich darüber auch beurteilen, ob die konkret gezogene Stichprobe verlässliche Informationen über die Grundgesamtheit liefert oder ob sie ein Ausreisser ist, der für Rückschlüsse auf die Grundgesamtheit untauglich ist.
In der folgenden Abb. III - 2 ist links eine hypothetische Grundgesamtheit mit den Parametern μ, σ und π und rechts eine möglich Stichprobe mit den Statistiken X̄, ŝ und p dargestellt. In der Mitte befinden sich die, aus den Parametern der Grundgesamtheit abgeleiteten Verteilungen dieser Stichproben-Statistiken.
Abbildung III-22: Die Stichprobenverteilungen als Brücke zwischen Grundgesamtheit und Stichprobe

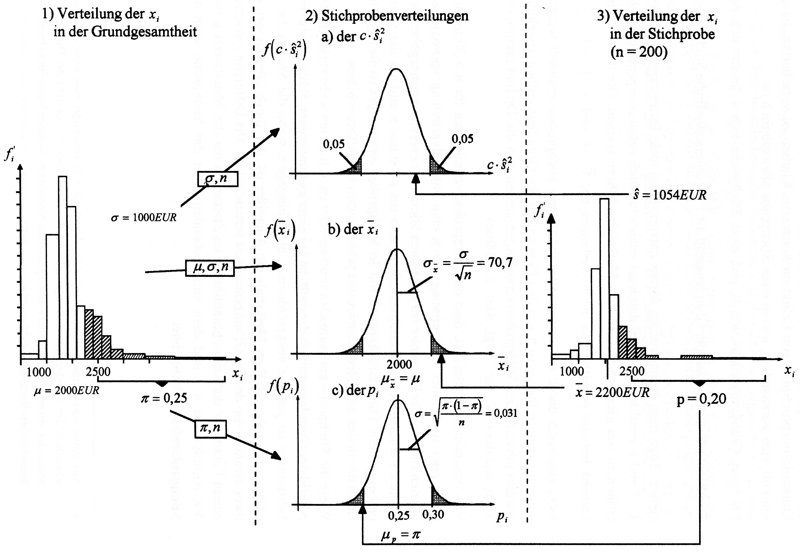
c) Die Ableitung der Parameter der Stichprobenverteilungen aus denen der Grundgesamtheit

Es ist sowohl plausibel wie wünschenswert, dass die Verteilungen der Mittel-, Streuungs- und Anteilswerte der Stichproben ihr Zentrum dort haben, wo der entsprechende Parameter der Grundgesamtheit liegt, d.h. dass E(X̄)= μ, E(ŝ) = σ und E(p) = π . Ist dies nicht der Fall, spricht man von einem Bias des Stichprobenparameters. Rückschlüsse von der Stichprobe auf die Grundgesamtheit führen dann tendenziell zu Fehlschlüssen.
Glücklicherweise können die notwendigen Informationen über die Stichprobenverteilungen, nämlich die über ihre Funktionsform (Binomial-, Normal-,- oder t- Verteilung) wie über ihre jeweiligen Parameter (Mittelwerte, Standardabweichungen, Freiheitsgrade) aus den Parametern der Grundgesamtheit und der Stichprobengröße abgeleitet werden.

d) Die Genese der Stichprobenverteilungen

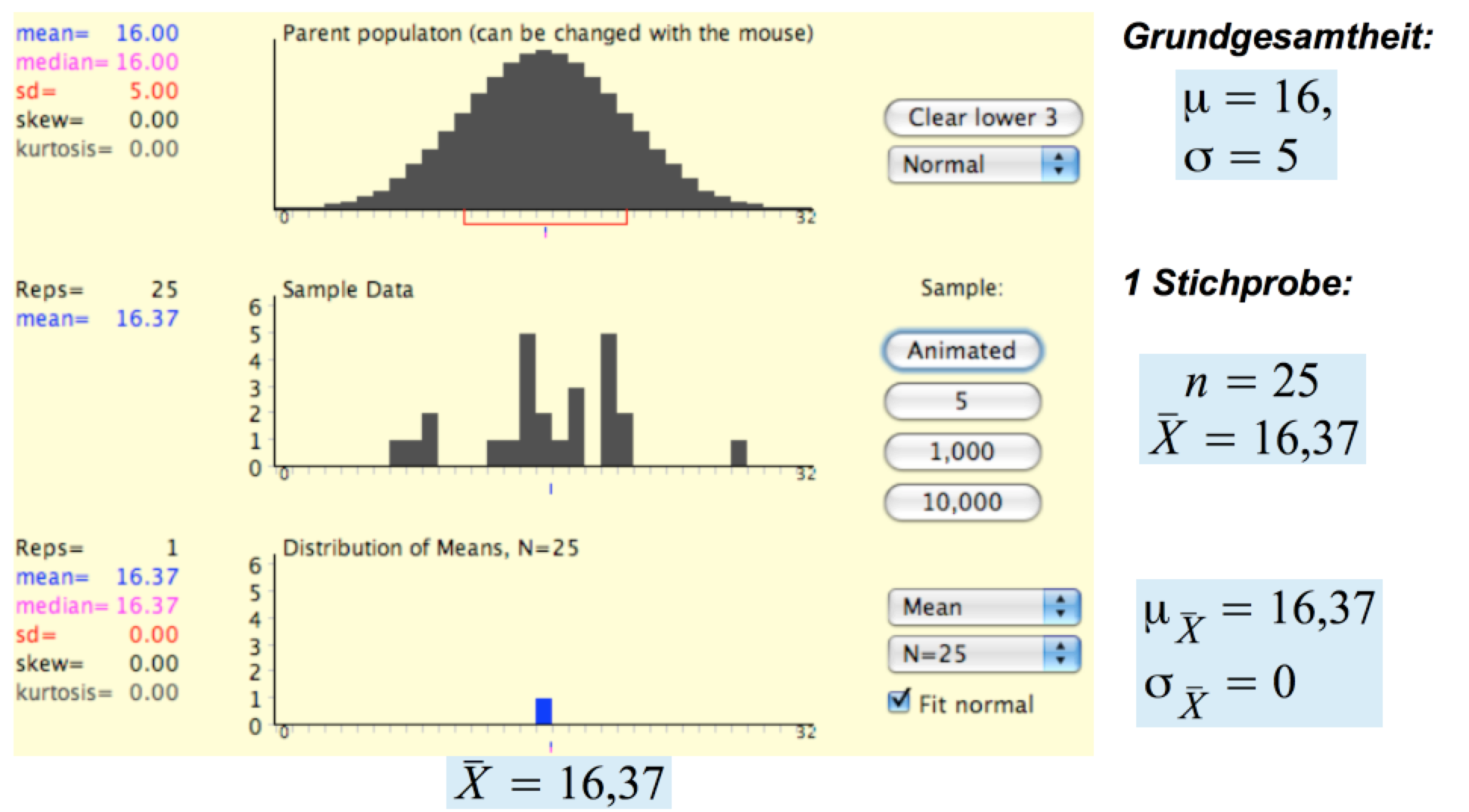
Wie in der Vorbemerkung betont könnten die Stichprobenverteilungen nur dann empirisch ermittelt werden, wenn alle denkbaren Stichprobenergebnisse und ihre Maßzahlen betrachtet werden. Mit einem Programm der Rice University lassen sich Stichprobenverteilungen erzeugen und graphisch darstellen sowie die dazu gehörigen statistischen Kennziffern der Verteilungen berechnen.eine Stichprobe im Umfang n = 25 gezogen. Da die Stichprobenverteilung nur aus einem Element besteht, ist der Mittelwert der Stichprobenverteilung identisch mit dem der Stichprobe (= 16,37).

Abbildung III-3a: Stichprobenverteilung bei einer simulierten Stichprobe

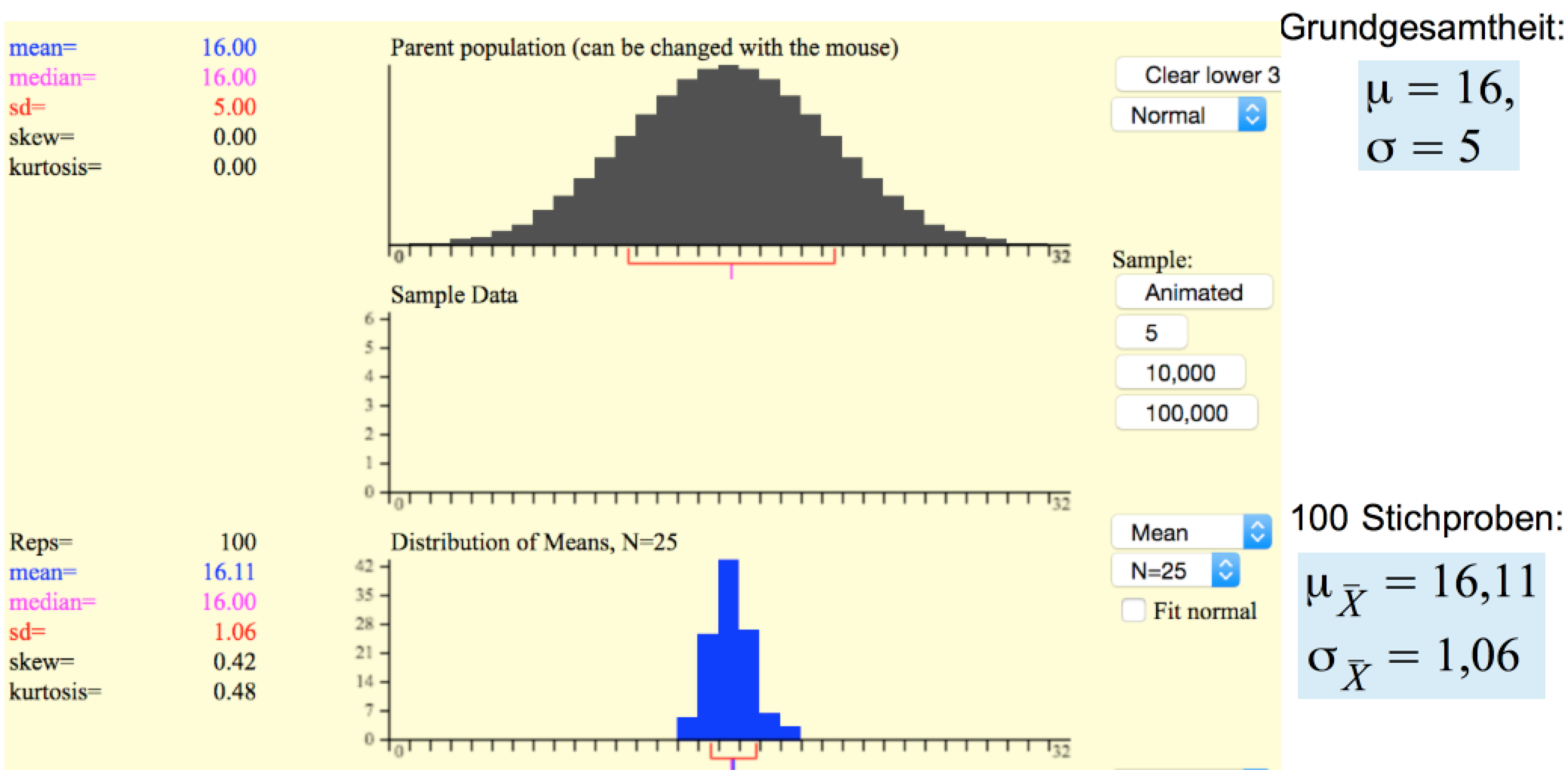
Der Abb. III-3b liegen 100 Stichproben zugrunde, so dass schon eine bessere Basis für eine Abschätzung der Stichprobenverteilung und ihrer Parameter gegeben ist.
Abbildung III-3b: Stichprobenverteilung bei 100 simulierten Stichproben

Hier liegt der Mittelwert der Stichprobenverteilung bereits näher am Mittelwert der Grundgesamtheit. Bemerkenswert ist aber auch, dass die Streuung der Mittelwerte fast um ein Fünftel geringer ist als die Streuung der Werte der Grundgesamtheit.

Mit diesem Programm der Rice University können Sie im Fenster "Begin" Stichprobenverteilungen aus unterschiedlichen, selbst definierten Grundgesamtheiten (1. Fenster), in selbstgewählten Schritten oder Anzahl von Stichproben (2. Fenster) für den Mittelwert sowie für weitere Parameter der Grundgesamtheit (3. und 4. Fenster) erzeugen, graphisch darstellen und die dazu gehörigen statistischen Kennziffern der Verteilungen berechnen.

d) Die Beurteilung von Ergebnissen einer Stichprobe

In Abb. III-2 ist ein innerer 90%-Bereich von Stichproben ausgewiesen, die noch mehr oder weniger akzeptable Schlüsse auf die Grundgesamtheit erlauben. Um Fehlschlüsse möglichst zu vermeiden, kann dieser Bereich zu Lasten der Genauigkeit des Schlusses auf 95% oder 99% ausgeweitet werden.
Danach stellt die betrachtete Stichprobe bezüglich ihres Mittel- und ihres Anteilswertes einen Ausreisser dar, wie er in 10% aller Fälle vorkommen kann. Ein Schluss von der Stichprobe auf die Grundgesamtheit würde nur bezüglich der Streuung der Grundgesamtheit nicht zu einem Fehlschluss führen.
Im Folgenden betrachten wir die Stichprobenverteilungen der Statistiken, für die wir in den nächsten Kapiteln die Grundlagen der Schlüsse von der Stichprobe auf die Grundgesamtheit einführen wollen.

Wählen Sie ein Modul: