1. Vorbemerkungen

• Die t-Verteilung wurde 1908 von Gosset unter dem Pseudonym „Student“ eingeführt. Sie ist daher bis heute auch unter der Bezeichnung „Student-Verteilung“ bekannt.

• Die (Student-) t-Verteilung dient in der induktiven Statistik als Basis der Verteilung von Stichprobenmittelwerten aus kleinen Stichproben und ist somit Grundlage der statistischen Schlüsse auf den entsprechenden Parameter.

2. Die t-Verteilung und ihre Eigenschaften

a) Die Dichtefunktion

• Die t-Variable ergibt sich aus dem Verhältnis einer standard-normalverteilten Zufallsvariablen und einer mitFreiheitsgraden-verteilten Zufallsvariablen:

  mitFreiheitsgraden.

• Die Dichtefunktionenwird hier in ihrer Funktionsform nicht wiedergegeben¹.

b) Parameter und Maßzahlen der Dichtefunktion

• Der einzige Parameter der Dichtefunktion ist die Anzahl der Freiheitsgrade .

• Der Erwartungswert der t-Verteilung ist erst abgegeben und beträgt dann:

  .

• Die Varianz der t-Verteilung kann abberechnet werden und beträgt:

  

c) Die graphische Darstellung der Dichtefunktion

Der Graph der t-Verteilung ist umsymmetrisch und ähnelt mit seiner Glockenform der Normalverteilung, allerdings verläuft er flacher als diese:

Abbildung II-13: Vergleich der Standardnormalverteilung mit einer Student t-Verteilung mit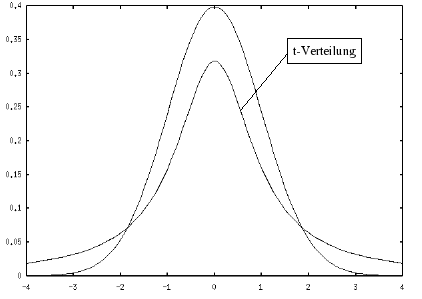

• Ein Rechner zur Bestimmung beliebiger Wahrscheinlichkeiten und zur Erzeugung einer Graphik findet sich unter diesem externen Link

• Eine grafische Darstellung der t-Verteilung liefert der t-Verteilung-Plotter von N. Johnston .

d) Die tabellierte Verteilungsfunktion

Die Randwahrscheinlichkeiten der t-Verteilung fürliegen ebenfalls in tabellierter Form vor. Ein Auszug für findet sich in Tab. II-6:

Tabelle II-6: Randwahrscheinlichkeiten der t – Verteilungfür

In der Tabelle sind die Freiheitsgrade in der Vorspalte zu finden, die kritischen Werte fürim inneren der Tabelle und die korrespondierenden Rand-Wahrscheinlichkeiten in den Spaltenüberschriften. Eine detaillierte Tabelle findet sich hier.

e) Die Approximation durch die Standard-Normalverteilung

Abist die t-Verteilung hinreichend genau durch die Standardnormalverteilung approximierbar. Es gilt dann:

1Zur Funktion und zu weiteren Einzelheiten vgl. Litz 2003 S.290 ff

---

Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 9 Benutzern im Durchschnitt mit "mittelmäßig" bewertet.

1/2 50 % Fortschritt

 

| Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächster Arbeitsschritt |