 |
Konzepte und Definitionen im Modul II-2 Die Normalverteilung
4. Die Gegenüberstellung von Normalverteilungen und anderen Verteilungen
a) Die Übereinstimmung einer empirischen Verteilung mit einer Normalverteilung
Wie in der Vorbemerkung betont, können empirische Verteilungen einer Normalverteilung entsprechen, wenn die Ausprägung des empirischen Merkmals von vielen Faktoren beeinflusst wird. Dies trifft oft auf persönliche Eigenschaften zu, wie etwa auf die Körpergröße oder den Intelligenzquotienten. Allerdings sind empirische Verteilungen
zufallsbedingt, so dass die Übereinstimmung meist nicht vollständig ist.
-
Ein graphischer Vergleich
Ob die Entsprechung der Verteilungen akzeptabel ist, wie etwa die für die Körpergrößen (vgl Abb. II-8a) oder eher nicht, wie etwa die für die Größe der Wohnungen (vgl Abb. II-8b) lässt sich oft schon an der Graphik erkennen, wenn über die empirische Verteilung eine Normalverteilungskurve mit den Parametern der empirischen Verteilung gelegt wird (mit SPSS z.B. leicht zu bewerkstelligen).
Abbildung II-8: Anpassung von empirischen Verteilungen an die Normalverteilung
|
Abb.II-8a: Körpergröße (m)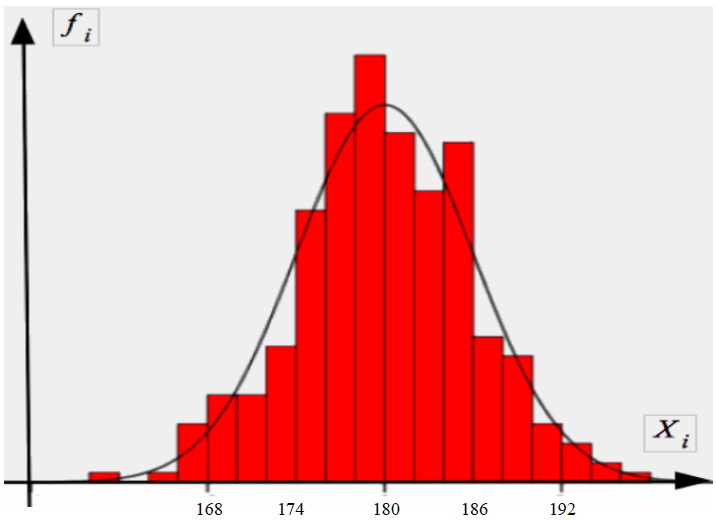 
|
|
Abb. II-8b: Wohnungsgröße
|
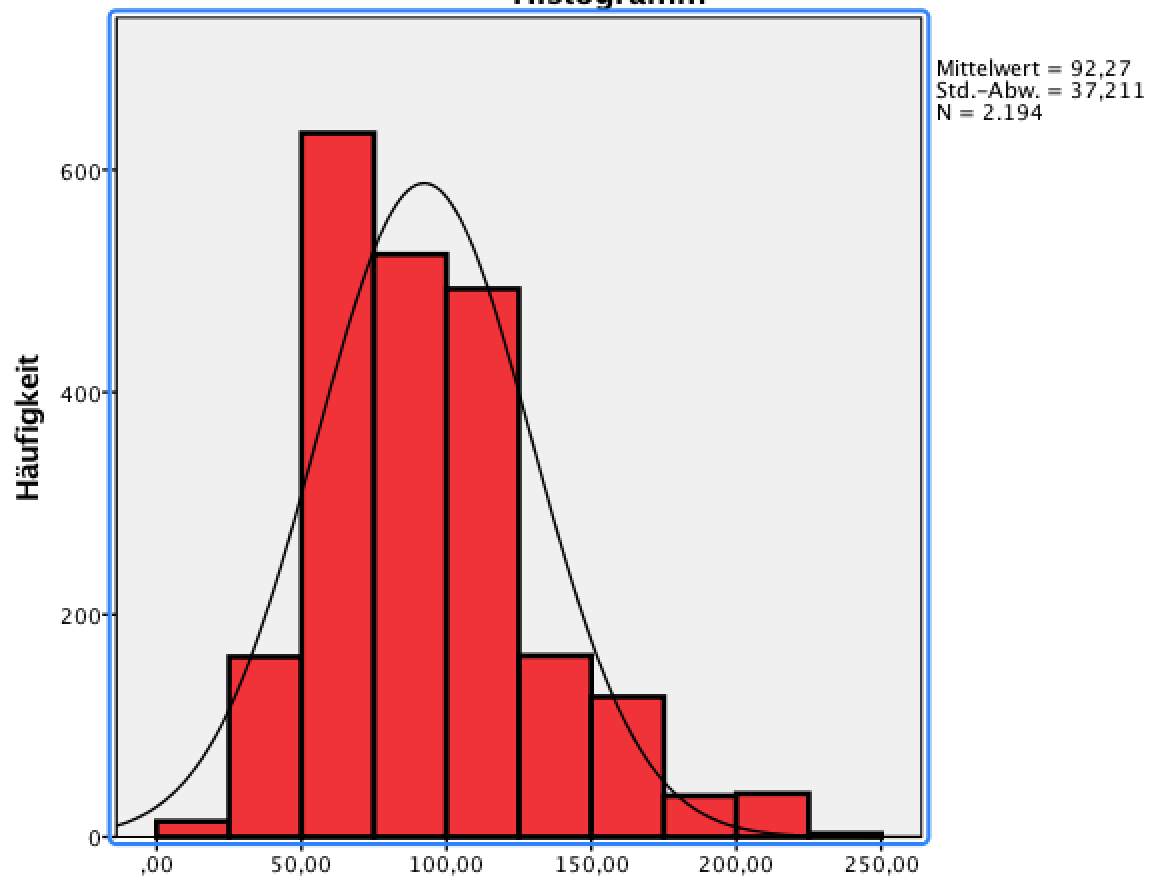
Die tabellarische Gegenüberstellung
Empirische Verteilungen liegen meist klassiert vor. Um die Häufigkeit einer derartigen Verteilung mit der Normalverteilung abgleichen zu können, müssen für die Normalverteilung (mit den Parametern der empirischen Verteilung) die Wahrscheinlichkeiten der Intervalle (aj ≤ X ≤ aj+1) ermittelt werden, die durch die Klassierung der empirischen Verteilung vorgegeben werden.
Dazu sind schrittweise die Wahrscheinlichkeiten
F1 = P(X ≤ a1), F2 = P(X ≤ a2)...... Fk =P(X ≤ ∞) und deren Differenzen
F2 - F1, F3 - F2,.... Fk - Fk-1
zu ermitteln.
Die Prüfung der Entsprechung der Verteilungen
Diese Differenzen sind den jeweiligen Wahrscheinlichkeiten der klassierten empirischen Verteilung gegenüber zu stellen. Ein Beispiel zum konkreten Vorgehen findet sich dazu im übernächsten Modul.
Im Kapitel Hypothesentest wird dann mit dem χ 2-Anpassungstest ein Verfahren zur exakten Beurteilung der Zufälligkeit oder Überzufälligkeit der Abweichungen zwischen den beiden Verteilungen beschrieben.
b) Die Approximation der Binomialverteilung
durch die Normalverteilung
Wie bereits im Modul zur Binomialverteilung ausgeführt und in der Abb. II-9 zu sehen ist, nähert
sich diese mit zunehmender Stichprobengröße, auch für
eine zunächst schiefe Verteilung immer mehr einer
symmetrischen Verteilung und schließlich einer Normalverteilung
an.
Da die Binomialverteilung für n > 20 in der Regel nicht mehr tabelliert wird, ist dies ist eine zentrale Bedingung für die Ermittlung von Wahrscheinlichkeiten von binomialverteilten Stichproben bei größeren Stichprobenumfang.
Abb. II-9: Binomialverteilung mit B(100, 0.1, 0.9)
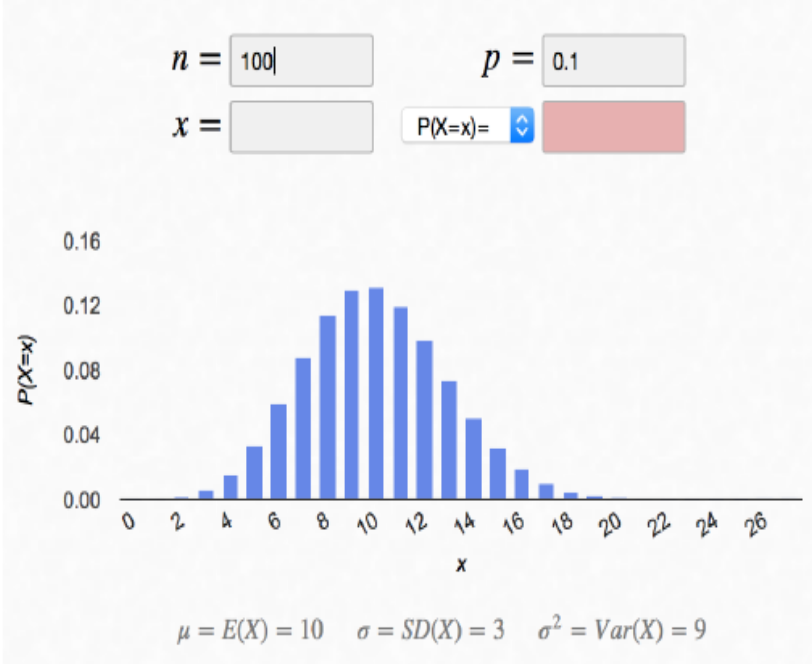
Die Prüfung der Approximationsbedingung
Die Binomialverteilung kann ab einer genügend
großen Varianz unter der folgenden Approximationsbedingung
durch die Normalverteilung angenähert werden:
VAR(K) = n · p · (1 - p) ≥ 9.
Für die Verteilung in Abb. II-9 ist diese Bedingung mit VAR(K) = n · p · (1 - p) = 100 · 0,1 · 0,9 = 9 bereits erfüllt.
Die Ermittlung der Parameter der Normalverteilung Ist obige Bedingung erfüllt, so entsprechen die Parameter der Normalverteilung den Parametern der Binomialverteilung, d.h.:
E(K) = n · p = μ und
σ (K) = √ {n · p · (1 - p)} = σ
Somit gilt
 .
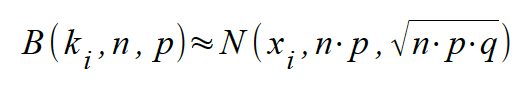Die Stetigkeitskorrektur
Weil die Binomialverteilung eine diskrete Verteilung mit Wahrscheinlichkeiten und die Normalverteilung eine stetige Verteilung mit Wahrscheinlichkeitsdichten ist, müssen die Werte der Binomialverteilung in Bereiche der Normalverteilung umgerechnet werden.
Einem diskreten ganzzahligen Wert ki der Binomialverteilung wird dabei eine Intervall xi ± 1/2 zugeordnet werden, damit die gesamte Fläche unter der Normalverteilungskurve abgedeckt werden kann (vgl. Abb. II-10).
Abbildung II-10: Flächen unter der Binomial-und der Normalverteilung
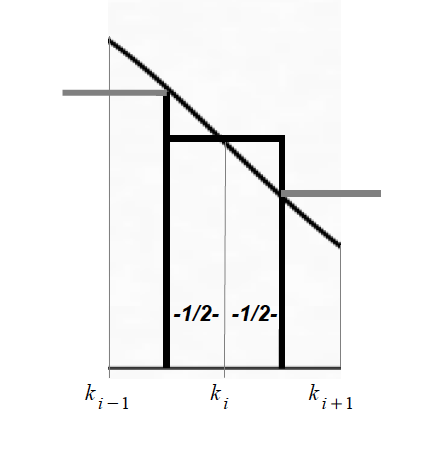
Für diesen Wert ki ergibt sich die
Wahrscheinlichkeit für ein Intervall mit den Grenzen a und b
als:
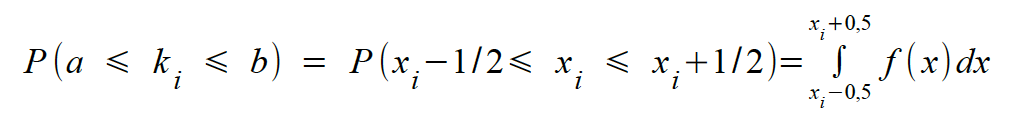
Die genaue Beachtung der Bereichsgrenzen
Dies ist notwendig, da sonst die Funktionswerte der Normalverteilung entweder zu groß oder zu klein ausfallen. Das Problem ist Abb. II-10 veranschaulicht. Je nachdem ob die genannte Ausprägung der binomischen Variablen in den abzuschätzenden Bereich mit einbezogen ist, also " ≥ " bzw. "≤" gilt oder ausgeschlossen ist, also ">" bzw "<" gilt, muss vom Wert xi der Betrag von 0,5 abgezogen oder zum Wert hinzu addiert werden. In der folgenden Übersicht sind die jeweiligen Möglichkeiten dargestellt.
Übersicht II-2: Berücksichtigung der Stetigkeitskorrektur
Die Standardisierung der zi -Werte
Die Werte der approximierten Normalverteilung
müssen wieder standardisiert, also in Z-Werte umgerechnet
werden, wenn mit Tabellen gearbeitet werden soll.
Dabei wird in den Fällen 1b) und 2a) mit folgender Formel gearbeitet:
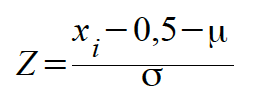
und in den Fällen 1a) und 2b) mit folgender Formel:
-
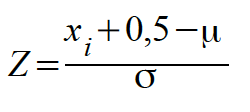
Mit F(X) ergibt sich die Wahrscheinlichkeit für rechte Bereiche (Fall 2. in Übersicht II-1)und
-
mit 1- F(X) ergibt sie sich für linke Bereiche (Fall 1. in Übersicht II-1).
Die verschiedenen Fälle sind in der Übersicht II-2 nochmals zusammgefasst, wobei in der Überschriftenzeile die Variablenbereiche der Binomialverteilung, in der 1. Spalte die dazu durchzuführenden Z-Transformationen und im Tabellenkern die daraus resultirenden Wahrscheinlichkeiten zu finden sind:
Übersicht II-2: Ermittlung der Randwahrscheinlichkeiten
Ein externes
Applet der Rice University
veranschaulicht die Approximationsgüte graphisch und rechnerisch
für unterschiedliche Bedingungen.
Zu weiteren Einzelheiten vgl. Litz 2003 S.384f
|
