 |
Konzepte und Definitionen im Modul II-1 Die Binomialverteilung
1. Vorbemerkungen
a) Die Struktur der Grundgesamtheit
Die Binomialverteilung ist eine diskrete Verteilung, die sich
durch Ziehung aus einer dichotomen
Grundgesamtheit ergibt. Dies bedeutet: Es gibt in der
Grundgesamtheit nur zwei mögliche Ereignisse
A und Ä.
Greift beispielsweise aus N Personen der GG eine Stichprobe von n
Personen heraus und befragt diese danach, ob sie ein eigenes Auto
besitzen, so ist dies eine Ziehung aus einer dichotomen
Grundgesamtheit. Es gibt nur zwei mögliche Ereignisse, nämlich
eine Person âbesitzt ein Autoâ und sie âbesitzt
kein Autoâ.
b) Die Struktur der Stichprobe
Aus dieser Grundgesamtheit resultiert die Binomialverteilung als
Folge einer daraus gezogenen Stichprobe: Wenn z.B.
15% der Bevölkerung älter als 65 Jahre sind, stellt sich
hinsichtlich eines Stichprobenergebnisses
die Frage: Wie wahrscheinlich es ist, in einer Stichprobe vom Umfang n
genau Personen zu finden, die älter als 65 Jahre sind?
Solche Ziehungen aus einer dichotomen Grundgesamtheit entsprechen
einem sog. Bernoulli-Experiment.
Dieses ist durch drei Eigenschaften gekennzeichnet:
Es gibt nur zwei mögliche,
einander ausschließende Ereignisse A und Ä.
Die Wahrscheinlichkeiten der
beiden Ereignisse sind beim Ziehen der Stichprobe konstant:
P(A) = p und P(Ä) = 1 - p = q
Die einzelnen Versuche
(Ziehungen) sind voneinander unabhängig.
Die zweite und dritte Bedingung werden als annähernd erfüllt
angesehen, wenn der Auswahlsatz weniger als 5% der Grundgesamtheit
ausmacht, also n/N < 0,05 ist.
Sind die obigen Bedingungen erfüllt, so ist die
Zufallsvariable K,
d.h. die gesucht Anzahl von Personen in der Stichprobe mit der
Eigenschaft A binomialverteilt.
Den jeweiligen Werten von ki werden
dann mit der Wahrscheinlichkeitsfunktion f(k i) = P(K = k i) die
Wahrscheinlichkeiten ihres Auftretens zugewiesen.
2. Die Eigenschaften der Binomialverteilung
a) Die Wahrscheinlichkeitsfunktion
Die Wahrscheinlichkeitsfunktion der Binomialverteilung
ergibt sich unter Berücksichtigung der Anzahl der möglichen
Kombinationen und der Eintrittswahrscheinlichkeiten der beiden
Ereignisse. Sie lautet:
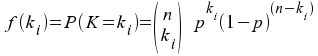 . .
Ihre Verteilung lässt sich in Kurzform
durch Angabe der relevanten Parameter k, n, p als B(k,n,p) charakterisieren.
Die Werte der Wahrscheinlichkeitsfunktion können
nach dieser Formel berechnet, aber für ausgewählte
Parameter auch direkt aus der tabellierten Binomialverteilung
abgelesen werden (vgl. dazu auszugsweise Tab. II-1).
Im Bernoulli-Experiment existieren nur zwei
mögliche Ereignisse, so dass P(k |A) = p und P(n - k | Ä) = p gleich
sind. Daher gilt die sog. Symmetrieeigenschaft:
B(k, n, p) = B(n - k, n, 1 - p)
b) Die Tabellierung der Wahrscheinlichkeitsfunktion
In der Regel sind die Werte der Binomialverteilung nur
für p ⤠0,5 tabelliert.
Wegen der oben erläuterten Symmetrieeigenschaft der
Binomialverteilung können die Werte auch für p > 0,5 aus
der Tabelle abgelesen werden. Einen Auszug aus einer solchen Tabelle
präsentiert Tab. II-1:
Tabelle II-1:
Wahrscheinlichkeitsfunktion der Binomialverteilung
(für n ⤠6 und ausgewählte p)
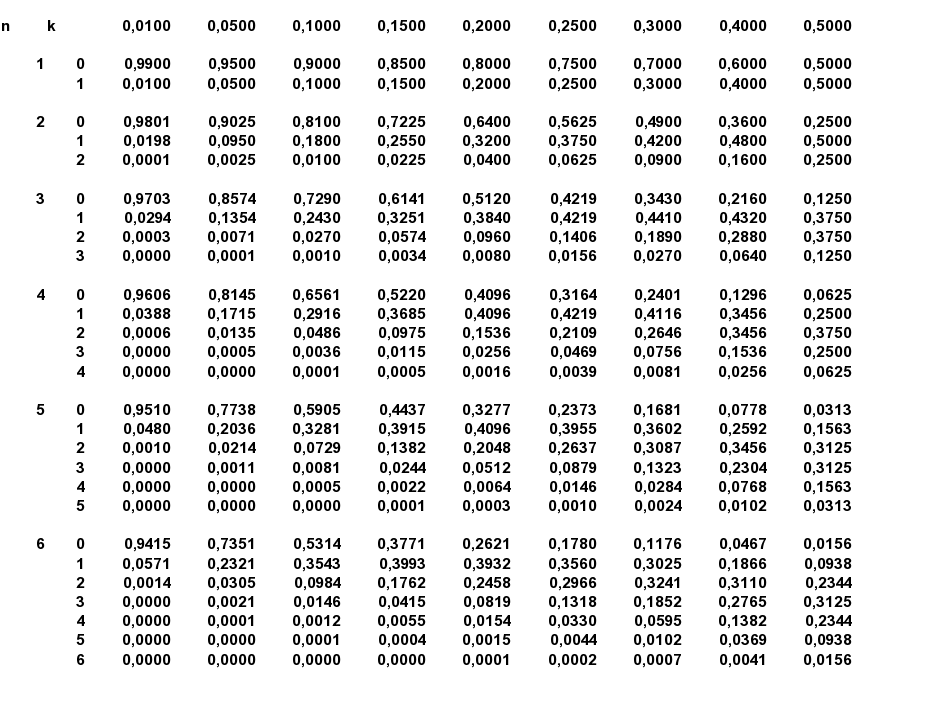
Eine ausführliche Tabelle der Wahrscheinlichkeiten finden Sie hier.
c) Die Parameter der Wahrscheinlichkeitsfunktion
Der Erwartungswert der
Binomialverteilung ergibt sich als
E(K) = n · p
Dies ist unmittelbar einleuchtend: Geht man beispielsweise davon
aus, dass 30% der Bevölkerung jedes Jahr an Grippe erkranken,
so erwartet man, dass von n = 1000 Personen einer Stichprobe
n · p = 300 Personen
krank werden.
Die Varianz der Binomialverteilung ergibt sich
mit:
VAR(K) = n · p · (1 - p)
Approximation der Binomialverteilung:
Für VAR(K) ⥠9 kann
die diskrete Binomialverteilung unter Beachtung einer
Stetigkeitskorrektur durch eine Normalverteilung approximiert werden
(vgl. dazu die Module zur Normalverteilung).
d) Die Verteilungsfunktion
Die Verteilungsfunktion der Binomialverteilung
gibt die Wahrscheinlichkeit dafür an, dass
K ⤠k0 ist:
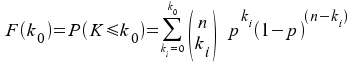
Ihre Werte ergeben sich durch Aufkumulieren der Werte
der tabellierten Wahrscheinlichkeitsfunktion.
e) Tabellarische und graphische Darstellung
-
Die Tabelle der Wahrscheinlichkeits- und der
Verteilungsfunktion
Für eine
Binomialverteilung mit p = 0,25 und n = 3 erhält man aus Zeilenblock 3 und Spaltenblock 6 der Tab. II-1 die Werte für Spalte 2 der folgenden Tabelle II-2. Die Werte der Verteilungsfunktion werden in Spalte 3 und 4 wiedergegeben:
Beispiel II-1: Wahrscheinlichkeits- und
Verteilungsfunktion
|
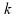
|
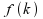
|
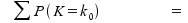
|
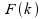
|
|
0
|
0,4219
|
0,4219
|
0,4219
|
|
1
|
0,4219
|
0,4219+0,4219
|
0,8438
|
|
2
|
0,1406
|
0,4219+0,4219+0,1406
|
0,9844
|
|
3
|
0,0156
|
0,4219+0,4219+0,1406+0,0156
|
1
|
Graphik der Wahrscheinlichkeits- und
Verteilungsfunktion
Die graphische Abbildung beider Funktionen ergibt:
Abbildung II-1: Wahrscheinlichkeits- und
Verteilungsfunktion
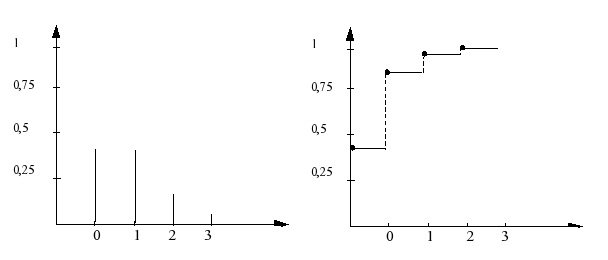
f) Interpretation der Werte
Was besagen nun z. B. die Werte in den Spalten 2 und 4 der obigen Tabelle II-2?
-
Die Werte der Wahrscheinlichkeitsfunktion (Spalte 2):
Nehmen wir an, eine Partei hat einen Wähleranteil von 25% (p = 0,25). Dann ist die Wahrscheinlichkeit unter 3 zufällig ausgewählten Personen keinen (k = 0)
Wähler dieser Partei zu finden etwa 42%: f(ki) = 0,4219 und die Wahrscheinlichkeit gleich 3 Wähler (k = 3) zu finden, knapp 1,6%: f(ki) = 0,0156.
Die Werte der Verteilungsfunktion (Spalte 4):
Hier finden sich die kumulierten Werte. Danach ist die Wahrscheinlichkeit unter 3 zufällig ausgewählten Personen höchsten einen (k ⤠1)
Wähler dieser Partei zu finden etwa 84%: F(k0)= 0,8438 und die Wahrscheinlichkeit höchstens 2 Wähler (k ⤠2) zu finden, etwa 98%: F(k0) = 0,9844).
|




