 |
Konzepte und Definitionen im Modul I-4 Zufallsvariablen und ihre Verteilung
1. Vorbemerkung
Bisher wurde weitgehend mit beliebigen Ereignissen operiert, wobei diese Ereignisse einen konkreten Sachverhalt betreffen konnten, z.B. "Es
wird eine rote Kugel gezogen", aber auch eine numerische Größe "Es wird eine "1" gewürfelt".
Zur Darstellung statistischer Ereignisse werden jedoch generell numerische Größen
benötigt, d.h.: die verschiedenen möglichen, nicht numerischen Ereignisse
müssen in Zahlen transformiert werden. Diese werden als Zufallsvariablen bezeichnet.
Eine Zufallsvariable
ergibt sich deshalb aus einer eindeutigen Zuordnung von Zahlen zu den
Ereignissen eines Zufallsexperimentes. Ihre Konstruktion basiert auf einem Definitionsbereich, der die Ereignisse beschreibt und einem Wertebreich, der die zahlenmäßigen Ausprägungen der Variablen umfasst.
Der Definitionsbereich der Variablen ist dabei der
Ereignisraum des Zufallsexperimentes,
Der Wertebereich der
Variablen besteht aus einer Menge von reellen Zahlen
Z = { x1, x2,......xk } ,
wobei gilt:, k ≤ n ,
da einer Ausprägung der Zufallsvariablen auch mehrere
Elementarereignisse zugeordnet werden können.
Dieser Sachverhalt sei an einem einfachen Beispiel verdeutlicht:
Beschreibung des Zufallsexperimentes: Aus einer Urne mit je einer roten und einer schwarzen Kugel sollen nacheinander 2 Kugeln gezogen werden, wobei die zuerst gezogene Kugel nach dem Zug zurückgelegt wird.
-
Beschreibung des Ereignisraums: Der Ereignisraum besteht aus folgenden Ereignissen:
-
rot im 1. Zug, rot im 2. Zug,
-
rot im 1. Zug, schwarz im 2. Zug,
-
schwarz im 1. Zug, rot im 2. Zug,
-
schwarz im 1. Zug, schwarz im 2. Zug
Bestimmung der Wahrscheinlichkeiten der Ereignisse: Da die gezogene Kugel zurückgelegt wird, sind die Wahrscheinlichkeiten aller vier Ereignis gleich:
P (ei) = 1/2 · 1/2 = 1/4
Definition der Zufallsvariablen: Die Zufallsvariable ist definiert als Anzahl der jeweils gezogenen roten Kugeln.
Wertebereich der Zufallvariablen: Der Wertebereich besteht aus den Ziffern 0, 1, 2, wobei dem Wert "2" das Ereignis 1 (aus dem obigen Ereignisraum), dem Wert "1" die Ereignisse 2 und 3 und dem Wert "0" das Ereignis 4 zugeordnet sind.
Wahrscheinlichkeiten des Zufallvariablen: Aus der Anzahl von Ereignissen, die den Werten der Zufallsvariablen zugeordnet werden können und ihren jeweiligen Wahrscheinlichkeiten folgt:
Eine graphische Veranschaulichung der Bestimmung der Wahrscheinlichkeitsverteilung ist in Abb. I-7 wiedergegeben:
Abbildung I-7: Definitions- und Wertebereich einer
Wahrscheinlichkeitsfunktion

Wie andere Variablen auch, können Zufallsvariablen in Form
stetiger und diskreter Variablen auftreten. Eine diskrete
Zufallsvariable ist eine Variable mit abzählbar endlichen
oder abzählbar unendlich vielen Ausprägungen. Eine stetige
Zufallsvariable ist eine Variable mit (nicht abzählbar)
unendlich vielen Ausprägungen. Wir beschäftigen uns
zunächst mit diskreten Zufallsvariablen:
2. Eigenschaften und Verteilung einer diskreten Zufallsvariablen
a) Die Wahrscheinlichkeitsfunktion
Eine diskrete Zufallsvariable ist somit eine veränderliche numerische
Größe, deren Ausprägungen xj jeweils
mit einer bestimmten Wahrscheinlichkeit f(xj) auftreten. Die Summe der Wahrscheinlichkeiten für alle möglichen
Werte der Zufallsvariablen ergibt immer Eins: ∑ f( xj) = 1 (j = 1 ... k)
.
Die allgemeine Form einer Wahrscheinlichkeitsfunktion
für eine diskrete Zufallsvariable lautet wie folgt:
f( xj ) = P (X = xj) = pj für xj ∈ Z
und
f( xj ) = P (X = xj) = 0 für xj ∉ Z
mit:
f( xj) ≤ 1 (j = 1 ... k) und ∑ f( xj) = 1 (j = 1 ... k)
b) Die Wahrscheinlichkeitstabelle
Die Werte einer Wahrscheinlichkeitsfunktion lassen sich auch tabellarisch darstellen. In einem einfachen Experimentes werden aus einem
Kartenstapel mit 4 Assen (A) und 6 Bildern (B) zwei
Karten gezogen. Die Ziehung erfolgt mit Zurücklegen. Der
Ereignisraum E umfasst damit die vier Elementarereignisse E = { AA, AB, BA, BB }.
Definieren wir nun die Zufallsvariable X als die Anzahl der gezogenen
Bilder, so kann diese Variable drei Werte annehmen:
"Null", "Eins" und "Zwei".
Damit ergeben sich für die
Wahrscheinlichkeitsfunktion f(x) = P(X = x i ) nach
dem Multiplikationssatz folgende Werte:
Tabelle I-1: Wahrscheinlichkeitsfunktion einer diskreten
Zufallsvariablen
c) Die Parameter der Funktion
Analog zur Häufigkeitsverteilung lässt
sich auch eine Wahrscheinlichkeitsverteilung durch Lage- und
Streuungsparameter charakterisieren:
Der Erwartungswert
entspricht von der Logik her dem Mittelwert der Verteilung. Er ist
definiert als:
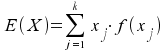
In obigem Beispiel erhalten wir:
E = 0 · 0,16 + 1 · 0,48 + 2 · 0,36 = 1,2 .
Es ist also zu erwarten, dass in diesem Experiment durchschnittlich
1,2 Bilder gezogen werden. Dieses Ergebnis zeigt auch, dass der
Erwartungswert nicht zwingen einen Wert ergeben muss, den die
Zufallsvariable tatsächlich annehmen kann.
Die Varianz wird
entsprechend als Mittelwert (Erwartungswert) der quadrierten
Abweichungen vom Erwartungswert berechnet, also als:
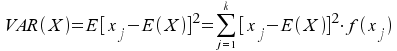
Sie kann wie in der deskriptiven Statistik umgeformt
werden:
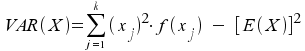
Im Beispiel ergibt sich (eingesetzt in die Rohformel) eine
Varianz von
VAR(X) = (0 - 1,2) 2 · 0,16 + (1 - 1,2) 2 · 0,48 + (2 - 1,2) 2 · 0,36 = 0,48
d) Die Verteilungfunktion
Neben der Wahrscheinlichkeitsfunktion, welche die
Wahrscheinlichkeit für das Auftreten jeder einzelnen möglichen
Ausprägung der Zufallsvariable bzw. der entsprechenden
Ereignisse angibt, ist auch von Interesse, mit welcher
Wahrscheinlichkeit die Zufallsvariable einen Wert in einem bestimmten
Bereich annimmt.
Die Verteilungsfunktion, gekennzeichnet mit einem
großen F, gibt dabei die Wahrscheinlichkeit dafür an, dass
X Werte kleiner oder gleich
x j annimmt. Sie entspricht damit der aufkumulierten
Häufigkeitsverteilung „...bis einschließlich X j
der deskriptiven Statistik.
Über die Verteilungsfunktion lässt sich auf einfache
Weise ermitteln, mit welcher Wahrscheinlichkeit die Zufallsvariable X
Werte zwischen zwei gegebenen Werten a und b annimmt:
P( a < X ≤ b ) = F (b - F(a))
Die allgemeine Form einer
Verteilungsfunktion für eine diskrete Zufallsvariable ist:
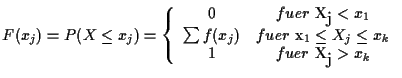
Die Werte der Verteilungsfunktion ergeben sich durch Aufkumulieren
der Werte der Wahrscheinlichkeitsfunktion, so dass wir für unser
Kartenexperiment erhalten:
Tabelle I-2: Verteilungsfunktion einer diskreten
Zufallsvariablen
|
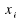
|
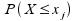
|
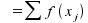
|
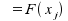
|
|
0
|
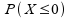
|
0,16
|
0,16
|
|
1
|
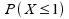
|
0,16+0,48
|
0,64
|
|
2
|
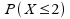
|
0,16+0,48+0,36
|
1
|
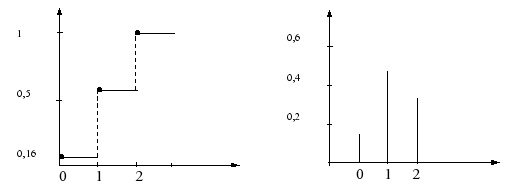
e) Die graphische Darstellung der Wahrscheinlichkeits- und Verteilungsfunktion
Die angemessene grafische Darstellungsform
der Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariable ist
das Stabdiagramm, die der Verteilungsfunktion die
Treppenkurve:
Abbildung I-8: Verteilungsfunktion und
Wahrscheinlichkeitsfunktion
|



