Konzepte und Definitionen im Modul I-3 Kombinatorik
1. Vorbemerkung
Bisher hatten wir die Anzahl der möglichen Ereignisse durch
Auszählen bestimmt, also den gesamten Ereignisraum eines
Zufallsexperimentes vollständig beschrieben und/oder grafisch
dargestellt. Allerdings zeigt sich schnell, dass dieses Vorgehen für
komplexere Zufallsexperimente insbesondere in mehrdimensionalen
Ereignisräumen ungeeignet, da zu aufwendig ist.
Dennoch besteht die Notwendigkeit, die Anzahl der möglichen
Ereignisse zu ermitteln, da die Wahrscheinlichkeit eines
Elementarereignisses ja definiert ist als:
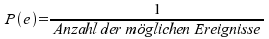 . .
Es werden also allgemeine Formeln zur Bestimmung der
Kombinationsmöglichkeiten unter verschiedenen
Ausgangsbedingungen benötigt. Dazu bedienen wir uns der
Kombinatorik.
Die möglichen Problemstellungen ergeben sich aus drei
Faktoren:
Wird die Gesamtheit oder nur eine Teilauswahl betrachtet?
Wird die Reihenfolge berücksichtigt ? und
Wird mit oder ohne Zurücklegen gezogen?
Daraus ergeben sich 6 unterschiedliche Aufgabenstellungen, von
denen jedoch nur 5 von Interesse sind, denn die Anzahl der
Kombinationsmöglichkeiten einer Gesamtheit von n Elementen ohne
Berücksichtigung der Reihenfolge ist logischerweise immer 1.
Die fünf unterschiedlichen Aufgabenstellungen sind in den folgenden Abschnitten dargestellt:
2. Die Auswahlmodelle
a) Permutationen
Unter Permutationen verstehen wir die Gesamtheit aller möglichen Anodnungen von n Elementen unter Berücksichtigung der Reihenfolge.
Die Frage ist: Wie viele Möglichkeiten gibt es, n Elemente
unter Berücksichtigung der Reihenfolge anzuordnen, also z.B. 5 Personen in eine Reihe zu stellen?
Die Antwort ergibt sich sehr einfach als Fakultät von n:
n ! (lies n-Fakultät), also: P n = n !
wobei P hier nicht für Wahrscheinlichkeit, sondern für eine
Permutation von n Elementen steht.
Berechnet wird die Fakultät von n als: n ! = n·(n-1)·(n-2)· ..... · 2·1
Dabei ist zu berücksichtigen, dass: n ! = n·(n-1)!
(Rekursiv–Formel)
und: 0 ! = 1 .
b) Variation mit Wiederholung
Unter einer Variationen mit Wiederholung versteht man eine Teilmenge, die durch Ziehung mit
Zurücklegen und mit Beachtung der Reihenfolge entseht.
Dazu wird aus n Elementen eine Teilauswahl von k Elementen
gezogen, wobei jedes gezogene Element wieder zurückgelegt
und die Reihenfolge der Ziehung berücksichtigt wird, also z.B. die verschiedenen Möglichkeiten nach dem Zufallsprinzip einen Totoschein auszufüllen. Dabei besteht n aus den Ziffern 1, 2 und 0 und k gibt die Anzahl der zu tippenden Spiele wieder.
Die Anzahl
der Möglichkeiten ergibt sich als:
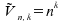
Da mit Zurücklegen gezogen wird (und damit beliebig oft),
kann k - wie beim Totoschein - größer als n sein.
c) Variation ohne Wiederholung (Kombination mit Berücksichtigung der Reihenfolge)
Unter einer Variation ohne Wiederholung bzw. Kombination mit Berücksichtigung der Reihenfolge versteht man eine Teilmenge, die durch Ziehung ohne Zurücklegen und mit Beachtung der Reihenfolge entsteht, also z.B. in einem Kaninchenzüchterverein mit n = 20 Mitgliedern zufällig den 1. und 2. Vorsitzenden, den Kassenwart und den Schriftführer auszulosen.
Wie oben werden unter Beachtung der Reihenfolge k aus n Elementen
gezogen, jedoch ohne die gezogenen Elemente zurückzulegen. Hierbei kann k höchstens so
groß wie n sein.
Die Anzahl der möglichen Variationen/Kombinationen ergibt sich als:
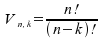
d) Stichproben ohne Zurücklegen (Kombinationen
ohne Zurücklegen und ohne Beachtung der Reihenfolge)
Im Gegensatz zu Variationen ohne Wiederholung werden nun alle
Kombinationen, die sich aus den gleichen k Elementen zusammensetzen
und sich nur durch die Reihenfolge unterscheiden als ein Fall
betrachtet.
Dies ist der Fall einer Zufallsstichprobe, bei der die Reihenfolge der gezogenen Elemente unerheblich ist, also z.B. für ein Volleyballmatch aus einem Spielerkader des Umfangs n die Mannschaft mit k = 6 Spielern nach dem Zufallsprinzip auszuwählen oder im Lotto sechs bezifferte Kugeln aus 49 bezifferten auszuwählen.
Die Anzahl der Kombinationen ergibt sich aus der Formel
für den Binomialkoeffizienten:
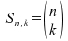 , ,
mit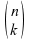 *) *)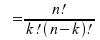 *) gelesen: n über k
*) gelesen: n über k
Für den Binomialkoeffizienten
gilt:
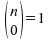 und und sowie sowie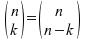
e) Stichproben mit Zurücklegen
Stichproben mit Zurücklegen sind eine Teilmenge, die aufgrund von
Ziehungen mit Zurücklegen und ohne Beachtung der Reihenfolge entstehen.
Der einzige Unterschied zu Fall 4 ist, dass nun jedes gezogene
Element wieder zurückgelegt wird. Diese Form der Stichproben ist eher selten, trifft aber zu bei Verkehrsstichproben, wo ein Fahrzeug u.U. mehrmals zufällig am Kontrollpunkt erfasst wird.
Die Zahl der
Kombinationsmöglichkeiten erhält man unter diesen
Bedingungen mit der Formel:
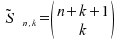
f) Permutationen von k und (n-k) gleichen Elementen
Eine spezielle Form von Permutationen sind die Permutationen eine Menge von n dichotomen Elementen, also z.B. den Möglichkeiten 5 rote und 3 blaue Spielsteine anzuordnen. In diesem Fall ist n = 8, k = 5 und n - k = 3. Die Anzahl der Möglichkeiten wird ebenfalls mittels des Binomialkoeffizienten
bestimmt: 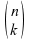 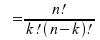
| 


