Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

1. Beispiele

a) Einfache (eindimensionale) Ereignisse

In einem 15 -köpfigen Vorstand mit 5 weiblichen und 10 männlichen Mitgliedern soll der Vorsitz nach dem Zufallsprinzip bestimmt werden. Wie groß sind die geschlechtsspezifischen Chancen?
Die Wahrscheinlichkeiten für die Wahl einer Frau bzw. eines Mannes für den Vorsitz ergeben sich nach dem klassischen objektiver Wahrscheinlichkeitsbegriff wie folgt:

und

b) Zweidimensionale Ereignisse

Ob Ereignisse abhängig oder unabhängig voneinander sind, hängt bei Auswahlexperimenten von der Ziehungsmodalität ab.

• Unabhängige Ereignisse

  Ein Beispiel: Eine Urne enthält drei rote und eine blaue Kugel. Gezogen wird mit Zurücklegen.

  Wie groß ist dann beispielsweise die Wahrscheinlichkeit, bei zwei aufeinander folgenden Ziehungen zweimal rot zu ziehen?

  

  Es gilt hier der Multiplikationssatz für unabhängige Ereignisse:

  

• Abhängige Ereignisse

  Wird jedoch ohne Zurücklegen gezogen, sind die Ereignisse abhängig voneinander, also:

  

  Es gilt hier der Multiplikationssatz für abhängige Ereignisse:

  

c) Mehrdimensionale Ereignisse

Fragestellungen wie dieses einfache Urnenexperiment werden sehr schnell komplexer, wenn sich die Anzahl der Ziehungen und der Elemente erhöht (wie wahrscheinlich wäre es etwa bei drei Ziehungen ohne Zurücklegen zwei rote und die eine blaue Kugel zu ziehen?).

Solche Probleme lassen sich mit Hilfe eines sog. Wahrscheinlichkeitsbaumes lösen:

Ein Beispiel: Ein 15 -köpfiger Vorstand wählt drei Sprecher aus. Von den 15 als Kandidaten in Frage kommenden Personen sind 10 männlich und 5 weiblich. Jeder Kandidat kann nur einmal gewählt werden.

Um die Wahrscheinlichkeit für die verschiedenen möglichen Konstellationen zu ermitteln wird der Wahrscheinlichkeitsbaum des Wahlvorganges benötigt (wobei die Wahl hier als Zufallsexperiment angesehen wird).

Abbildung I-6: Wahrscheinlichkeitsbaum

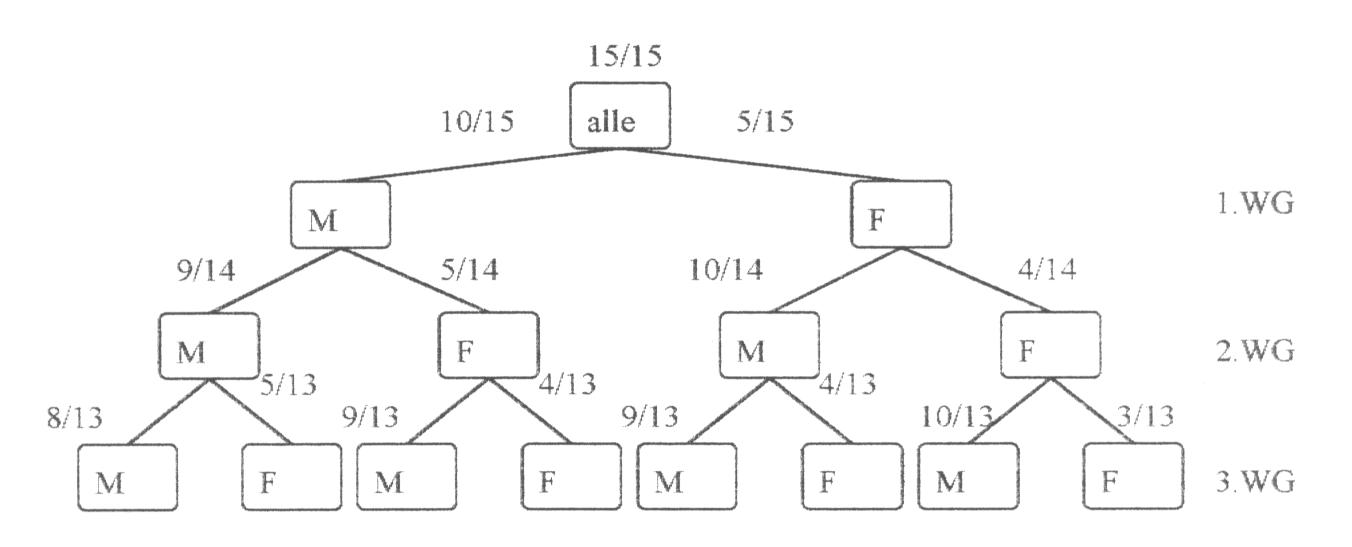
Soll die Reihenfolge der Wahl der Kandidaten nicht berücksichtigt werden, so müssen die Wahrscheinlichkeiten entlang der Äste des Baums multipliziert sowie die Wahrscheinlichkeiten der Äste, die zu gleichen Konstellationen führen addiert werden.

So ergibt sich beispielsweise als Wahrscheinlichkeit, dass drei Männer gewählt werden:

Dies ist die einfachste Variante, da es nur einen Ast (in der Abb. der linke) gibt, der zu verfolgen ist.

Anders bei der Konstellation „ein Mann, zwei Frauen''. Hier gibt es drei Äste mit:

d) Das Ziegenproblem - Ein Spiel mit der Wahrscheinlichkeit

• Spielregeln: Es gibt drei Türen. Hinter einer befindet sich der Geldgewinn, hinter den beiden anderen eine Niete (hier ein fußlahmer Esel). Im ersten Schritt entscheidet sich der Kandidat für eine der drei Türen. Danach öffnet der Moderator eine der beiden anderen Türen, hinter der sich eine Niete befindet. Daraufhin kann sich der Kandidat entscheiden, ob er bei der zuerst gewählten Tür bleibt, oder sich für die andere Tür entscheidet.

• Frage: Wann hat der Kandidat die besseren Chancen auf den Hauptgewinn? Wenn er bei seiner ersten Entscheidung bleibt, oder wenn er die Tür wechselt?

• Graphische Veranschaulichung der SPIELANLAGE:

  1. Schritt: Ein Quizzmaster zeigt dem Kandidaten 3 Türen, wobei sich hinter einer Tür ein Schatz und hinter zwei Türen jeweils ein Esel befindet.

  

  2. Schritt: Der Kandidat wählt Tür 1: Wie groß ist die Wahrscheinlichkeit, dass der Kandidat den Schatz gewählt hat?

  

  Die Wahrscheinlichkeit, dass der Kandidat mit Tür 1 den Schatz gewählt hat, ist offensichtlich 1/3.

  3. Schritt: Der Quizzmaster öffnet nun nicht die Tür 1 sondern die Tür 3, hinter der ein Esel steht und fragt den Kandidaten, ob er jetzt von der Tür 1 auf die Tür 2 wechseln will, um seine Gewinnchancen zu erhöhen.

  

  4. Schritt: Frage: lohnt es sich zu wechseln oder ist das für die Gewinnchance egal?
  
  

• Eine erste anschauliche Lösung zeigt die folgende Abbildung:.

  

  Danach verdoppelt sich die Gewinnchance auf 2/3, wenn der Kandidat von der Tür 1 zur Tür 2 wechselt.

• Eine formelmäßige Lösung basiert auf dem Satz von Bayes (vgl. dazu auch den nachfolgenden Hinweis).

• In dem folgenden Applet "Let's make a deal" der University of California, San Diego können Sie selbst Ihr Glück versuchen.

2. Aufgaben

a) Aufgaben zum Begriff der Wahrscheinlichkeit

Wie wir gesehen haben, sind Wahrscheinlichkeiten in unterschiedlichen Kontexten unterschiedlich zu definieren

Nach welchem Konzept also würden Sie P(A) bestimmen für:

• A = „Kopf" beim Münzwurf

• B = „Kopf" beim Werfen einer Reißzwecke

• C = Sieg eines bestimmten Teams in einem Fußballspiel?

b) Aufgaben zu Wahrscheinlichkeitsoperationen

Im Folgenden haben Sie die Möglichkeit, Wahrscheinlichkeitsoperationen anhand von vorgegebenen Aufgabenstellungen durchzuführen und anhand bereitgestellter Musterlösungen zu überprüfen. Dazu finden Sie am Ende dieser Seite einen Link auf die Musterlösungen zu diesen Aufgaben.

Aufgabe (1)
Im Zusammenhang einer Erhebung über den Energieverbrauch privater Haushalte seien folgende Ereignisse definiert:

• A: ein Haus ist aus Ziegeln gebaut

• B: Es ist mehr als 30 Jahre alt

• C: Ein Haus wird mit Öl geheizt.

1. Wenn Sie den Ereignissen Flächen zuweisen, deren Größe der vermuteten realen Bedeutung entspricht

   1. Welche Größenordnung ergibt sich für die Gesamtflächen und die Schnittflächen?

   2. Woraus resultiert die räumliche Zuordnung der Flächen zu A, B und C?

2. Beschreiben Sie die folgenden Ereignisse als zusammengesetzte Ereignisse, Schnittmengen und Komplemente und stellen Sie sie graphisch dar:

   1. Ein Haus ist mehr als 30 Jahre alt und wird mit Öl beheizt.

   2. Ein Haus ist nicht aus Ziegeln gebaut.

   3. Ein Haus wird mit Öl beheizt oder ist älter als 30 Jahre.

   4. Ein Haus ist aus Ziegeln gebaut und wird nicht mit Öl beheizt.

   5. Welchem Ereignis ist ein neues, elektrisch beheiztes Holzferienhaus zuzuordnen?

c) Aufgaben zur Wahrscheinlichkeitsrechnung

Im Folgenden haben Sie die Möglichkeit, Wahrscheinlichkeiten anhand von vorgegebenen Aufgabenstellungen zu berechnen und Ihre Berechnungen anhand bereitgestellter Musterlösungen zu überprüfen. Dazu finden Sie am Ende dieser Seite einen Link auf die Musterlösungen zu diesen Aufgaben. In der dort präsentierten Musterlösung zur Aufgabe 5 findet sich auch eine wahrscheinlichkeitstheoretisch begründete Behandlung des Ziegenproblems.

Aufgabe (2)
In einem Raum befinden sich fünf wahlberechtigte Personen, von denen bei der nächsten Wahl drei ,,blau" und zwei ,,gelb" wählen wollen. Die Blauwähler sind mit den Zahlen eins, zwei und drei, die Gelbwähler mit den Zahlen vier und fünf gekennzeichnet. Als Menge notiert haben wir also E = {B₁, B₂, B₃, G₄, G₅}. Es werden jetzt Experimente in Form einer Auswahl einer oder mehrerer Personen durchgeführt.

Zunächst wird eine Person ausgewählt

1. Wie groß ist die Wahrscheinlichkeit, den Gelbwähler mit der Nummer 4 auszuwählen?

2. Wie groß ist die Wahrscheinlichkeit, einen Blauwähler auszuwählen?

3. Wie groß ist die Wahrscheinlichkeit, einen Blauwähler oder einen Gelbwähler auszuwählen?
   Nun werden nacheinander zwei Wähler ausgewählt, der erste jedoch vor Auswahl des zweiten zurückgelegt

4. Wie sieht der Ereignisraum aus?

5. Wie groß ist die Wahrscheinlichkeit, in beliebiger Reihenfolge einen Gelbwähler und einen Blauwähler zu ziehen?

6. Wie groß ist die Wahrscheinlichkeit, zuerst einen Gelbwähler, dann einen Blauwähler zu ziehen?

7. Wie groß ist die Wahrscheinlichkeit, fünf als Summe der Nummern der beiden Wähler zu erhalten?
   Nun werden nacheinander (ohne Wiederholung) zwei Wähler gezogen

8. Wie sieht der Ereignisraum für dieses Experiment aus?

9. Wie groß ist die Wahrscheinlichkeit, einen Gelbwähler und einen Blauwähler zu ziehen?

10. Wie groß ist die Wahrscheinlichkeit, zuerst einen Gelbwähler, dann einen Blauwähler zu ziehen?
    Beim letzten Experiment werden nacheinander (mit Wiederholung) drei Wähler ausgewählt

11. Sowohl bei der ersten, als auch bei der zweiten Ziehung wird je ein Gelbwähler gezogen. Wie groß jetzt ist die Wahrscheinlichkeit, bei der dritten Ziehung ebenfalls einen Gelbwähler zu erhalten?

Aufgabe (3)
Bei einem zweimotorigen Flugzeug der Firma Sicherheit fällt im Laufe der Gesamtlebenszeit mit einer Wahrscheinlichkeit von 0,001 das Triebwerk 1 und mit einer Wahrscheinlichkeit von ebenfalls 0,001 das Triebwerk 2 aus. Mit einer Wahrscheinlichkeit von 0,0001 fallen beide Triebwerke unmittelbar nacheinander aus.

1. Wie groß ist die Wahrscheinlichkeit, dass keines der Triebwerke ausfällt? Stellen Sie dieses Ereignis im Venn -Diagramm dar

2. Sind die beiden Ereignisse von einander unabhängig?

3. Wie groß ist die bedingte Wahrscheinlichkeit für den Ausfall eines zweiten?

Aufgabe (4)
Ein Betriebsrat, der aus zehn Männern und fünf Frauen besteht, wird einen dreiköpfigen Sprecher(innen)rat wählen.

1. Bei einem überbetrieblichen Vergleich stellt sich heraus, dass in nur 60 % aller vergleichbaren Fälle das Geschlechterverhältnis des Sprecher(innen)rats dem des Betriebsrates entspricht (nämlich 2:1) und dass in 25 % aller Fälle sogar nur Männer im Sprecherrat vertreten sind. Kann man aus den gegebenen empirischen Daten folgern, dass in der Mehrzahl der Wahlen die Männer die größeren Chancen hatten? Antworten Sie spontan!

2. Berechnen Sie nun die Wahrscheinlichkeit, dass dem Sprecher-Rat 1) kein Mann, 2) ein Mann, 3) zwei Männer, 4) drei Männer angehören? (Für jede Person wird jeweils ein Wahlgang durchgeführt.)

Aufgabe (5)
In einem Quizprogramm können die Kandidaten eine von drei verschlossenen Türen auswählen, bei denen hinter einer der Hauptgewinn, ein Auto, und hinter den anderen beiden die Nieten, je eine Ziege, warten. Nach dem sich der Kandidat für eine der Türen (z.B. A) entschieden hat, öffnet der Showmaster nun nicht die gewählte Tür (A), sondern eine andere (C), von der er weiß, dass dahinter eine Ziege steht, und bietet dem Kandidaten an, seine ursprüngliche Wahl (A) nochmals zu überdenken. Verbessert oder verschlechtert der Kandidat seine Chancen auf den Hauptgewinn, wenn er sich nun für Tür (B) entscheidet oder bleiben die Chancen gleich?

Aufgabe (6)
Ein Vater sagt zu seinem Sohn: ,,Du bekommst mehr Taschengeld, wenn Du von drei Tennispartien, die Du abwechselnd gegen mich und Deine Mutter spielst, zwei hintereinander gewinnst." Die Wahrscheinlichkeit des Sohnes, gegen seinen Vater zu gewinnen, betrage 0,5; da die Mutter eine schwächere Tennisspielerin ist, betrage die Wahrscheinlichkeit eines Erfolges des Sohnes über die Mutter 0,8. Die Ergebnisse der einzelnen Spiele seien als unabhängig von einander anzusehen.
Berechnen Sie die Wahrscheinlichkeit einer Taschengelderhöhung für die Fälle, dass der Sohn erst gegen den Vater antritt, danach, dass er erst gegen die Mutter spielt. Bei welcher Entscheidungsalternative hat der Sohn die größeren Chancen? Zeigen Sie die Rechenwege klar auf!

Aufgabe (7)
Drei Maschinen A, B und C produzieren 50%, 30% bzw. 20% der gesamten Produktion eines Betriebes. Die Ausschussanteile der Maschinen betragen 3%, 4% bzw. 5%.

1. Wie groß ist die Wahrscheinlichkeit für das Ereignis: ,,ein zufällig ausgewähltes Stück ist defekt"?

2. Wie groß ist die Wahrscheinlichkeit für das Ereignis: ,,ein zufällig ausgewähltes defektes Stück stammt von Maschine A"?

Aufgabe (8)
Der Datenreport 1992 (Stat. Bundesamt (Hrsg.): Datenreport 1992, S.86) meldet für das Jahr 1989, dass aus Arbeiterhaushalten ca. 9 % der 10-15jährigen Kinder aufs Gymnasium gehen. Aus Angestelltenhaushalten sind es ca. 35 %, aus Beamtenhaushalten ca. 45 % und aus Selbständigenhaushalten ca. 32 %. Der Anteil der einzelnen Haushaltstypen an der Gesamtzahl der Herkunftshaushalte beträgt 38 % bei den Arbeiterhaushalten, 44 % bei den Angestelltenhaushalten und je 9 % bei Beamten- und Selbständigenhaushalten.
Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewähltes Kind auf das Gymnasium geht?
Wie groß ist die Wahrscheinlichkeit, dass es aus einem Angestellten- bzw. aus einem Arbeiterhaushalt stammt?

Zur Musterlösung der Aufgaben (1) bis (8)

letzte Änderung am 5.4.2019 um 4:24 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel01_Grundlagen~~lder~~l~~lWahrscheinlichkeitsrechnung/modul02_Begriffe~~lund~~lAxiome~~lzur~~lWahrscheinlichk
eit/ebene02_Beispiele~~lund~~lAufgaben/01__02__02__01.php3