 |
Konzepte und Definitionen im Modul I-1 Zufallsereignisse und Ereigniskalküle
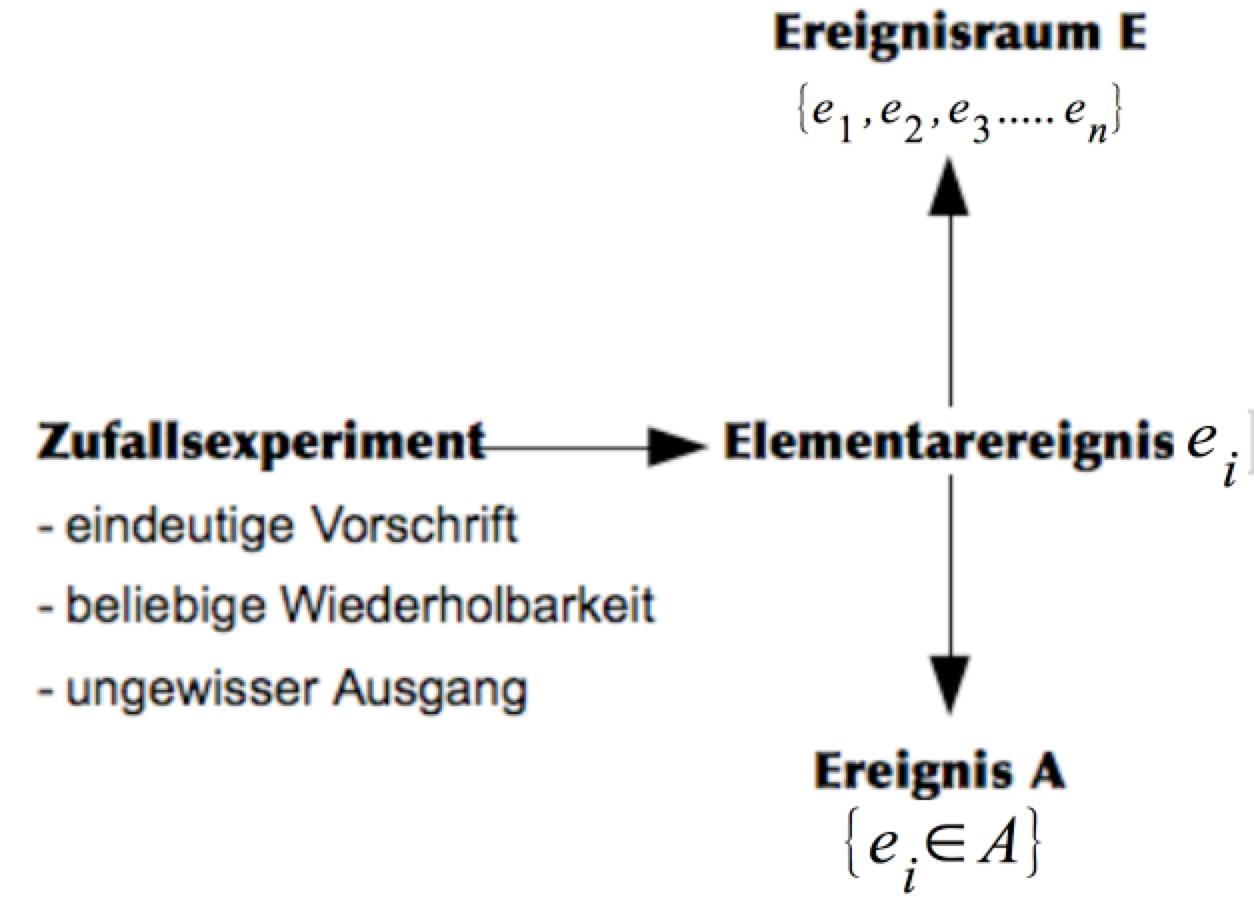
1. Die Zufallsstichprobe als Zufallsereignis
Zufallsereignisse sind Ergebnisse eines Zufallsprozesses. Dieser ist
gekennzeichnet durch:
eine bestimmte
Regelhaftigkeit der Durchführung,
die beliebige Wiederholbarkeit
des Ablaufs und
die Unvorhersehbarkeit seines
konkreten Resultats.
Gängige Beispiele sind das Werfen einer Münze oder eines
Würfels, das Ziehen einer Karte aus einem Stapel und die
zufällige Auswahl einer Person aus einer Personengruppe.
2. Das System der Zufallsereignisse
Die Gesamtheit aller möglichen Ereignisse wird als Ereignisfeld
oder als Ereignissystem bezeichnet.
Man unterscheidet dabei in nicht weiter zu differenzierende
Elementarereignisse und in zusammengesetzte Ereignisse.
a) Elementarereignisse und Ereignisräume
Elementarereignisse ei
sind
solche Ereignisse, die sich nicht weiter aufspalten lassen. Also z.B. eine bestimmte Augenzahl als Ergebnis eines Würfelwurfs.
Die Menge
aller Elementarereignisse bilden den Ereignisraum E des
Zufallsexperimentes, beim Wurf eines einzelnen sechsflächigen
Würfels also E = {1, 2, 3, 4, 5, 6}.
b) Zusammenegesetzte Ereignisse und Ereignisräume
Wir können jedoch auch Ereignisse definieren, die mehrere
Elementarereignisse enthalten. Legen wir fest, das Ereignis A
sei eingetreten, wenn eine Zahl größer 3 gewürfelt
wird, enthielte A drei Elementarereignisse, also A = {4, 5, 6}.
Sobald also als Ergebnis des Zufallsexperimentes eines dieser
Elementarereignisse eintritt, tritt auch das Ereignis A ein.
Die
bisherigen Zusammenhänge sind in der nachfolgenden Übersicht
zusammengefasst:
Abbildung I-2: Zufallsexperimente und Ereignisse
c) Ereignistypen
Neben
den Elementarereignissen und Ereignissen, die mehrere
Elementarereignisse enthalten, sind die folgenden Ereignistypen
zu unterscheiden, jeweils illustriert am Beispiel eines einfachen
Würfelwurfs:
Das
Teilereignis B ⊂ A:
Ist A definiert als Augenzahl größer 2 und B als
Augenzahl größer 5, so wäre B Teilereignis von A.
Das
Sichere Ereignis S besteht
im Wurf einer Augenzahl zwischen 1 und 6. Dieses Ereignis tritt in
jedem Fall ein.
Das
unmögliche Ereignis ∅ wäre
z. B. ein Wurf einer Augenzahl größer 6. Dieses Ereignis
tritt in keinem Fall ein.
Das
komplementäre Ereignis Ā umfasst
den gesamten Bereich des Ereignisraumes E, der nicht dem Ereignis A
zugeordnet ist. Wenn A = {2 ,4 ,6},
also die geraden Augenzahlen beinhaltet, so ist Ā = {1, 3, 5} und
umfasst die ungeraden Augenzahlen.
Disjunkte
Ereignisse sind solche
Ereignisse, zwischen denen keine Schnittmenge existiert, die sich
also gegenseitig ausschließen, z.B.: A = {1,2,3} und B = {5, 6}.
Äquivalente
Ereignisse A = B sind Ereignisse mit identischen
Elementarereignissen, also das Ereignis A mit : A = {2, 4, 6} und
das Ereignis B, das alle geraden Augenzahlen umfasst.
d) Ereignisoperationen
Die
Verknüpfung von Ereignissen erfolgt über
Ereignisoperationen. Diese entsprechen denen der allgemeinen
Mengenlehre. Ereignisse lassen sich graphisch in Form von Venn-Diagrammen
darstellen. Dabei wird der Ereignisraum d.h. die Menge aller
Elementarereignisse als Rechteck, die über dem Raum definierten
Ereignisse als beliebige Teilflächen dieses Rechtecks
ausgedrückt.
Wir definieren als:
Schnittmenge
(UND-Verknüpfung) zweier Ereignisse das gemeinsame Auftreten zweier Ereignisse A und B und schreiben
C = A ∩ B,
Abbildung I-3a: Darstellung der Schnittmenge im Venn-Diagramm
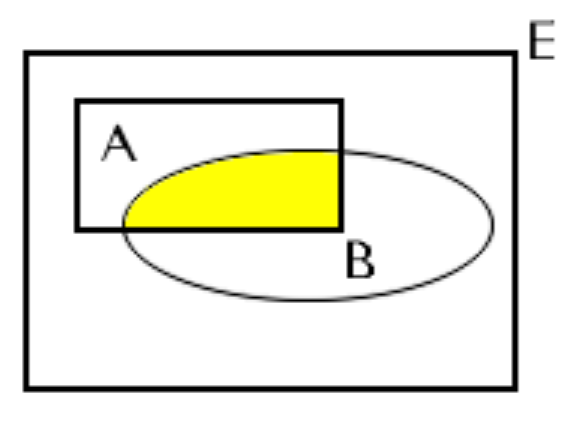
Sind A und B disjunkt, gilt: A ∩ B = ∅.
Vereinigungsmenge
(ODER-Verknüpfung) das Auftreten des Ereignisses A odes des Ereignisses B und schreiben : C = A ∪ B
Abbildung I-3b: Darstellung der Vereinigung im Venn-Diagramm
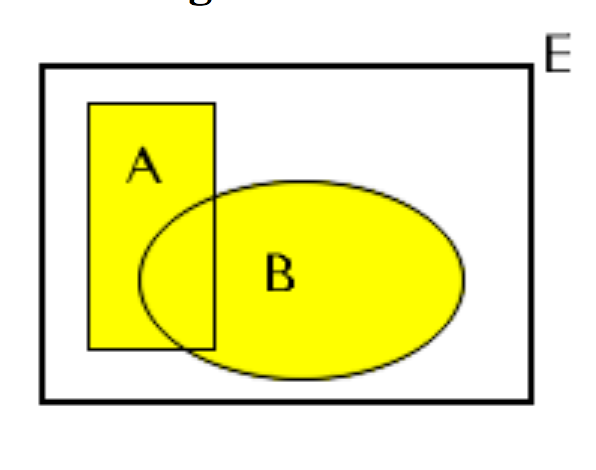
Es gilt: A ∪ Ā = S.
Differenz
zweier Ereignisse das Auftreten des Ereignisses A ohne deren Elemente in B und schreiben: C = A - B.
Abbildung I-3c: Darstellung der Differenz im Venn-Diagramm
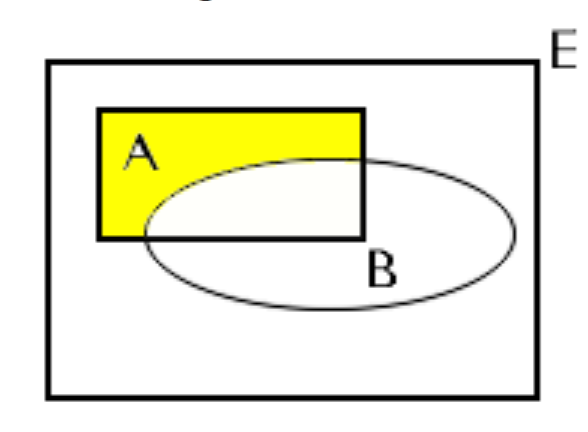
Die
Definitionen zu den Ereignistypen und -operationen sind in der nachfolgenden Übersicht
zusammengefasst:
Übersicht I: Ereignistypen und -operationen

3. Zweidimensionale Zufallsereignisse
Die
Dimensionalität von Ereignissen bezeichnet die
Häufigkeit, mit der ein Experiment durchgeführt wird, also
z.B. die Anzahl gemeinsam oder hintereinander geworfener Würfel
oder die Anzahl aus einem Stapel gezogener Karten.
Zweidimensionale Ereignisse sind demnach Ereignisse, die zweimal ausgeführt werden, also z.
B. einen Würfel zweimal zu werfen oder zwei Würfel zu werfen.
Ein zweidimensionales Ereignis wäre also das Ereignis zweimal eine "6" zu werfen.
Zwei- und mehrdimensionale Ereignisse werden im Modul zur Wahrscheinlichkeitsrechnung ausführlicher behandelt.
|



