 |
Konzepte und Definitionen im Modul XII-7 Die mehrfaktorielle Varianz- und Kovarianzanalyse
Vorbemerkung
In den folgenden beiden Abschnitten wird
das einfache varianzanalytische Modell auf einen zwei- und mehrfaktoriellen Ansatz ausgeweitet.
Im kovarianzanalytischen Modell werden die Regressions- und die Varianzanalyse in einem Modellansatz zusammengeführt und somit ein Allgemeines Lineares Modell (ALM) entwickelt.
1. Die zwei- und mehrfaktorielle Varianzanalyse
a) Die Modellkomponenten
Im zwei- und mehrfachen varianzanalytischen Modell wird der Zusammenhang zwischen einer abhängigen metrischen Variablen und mindestens zwei unabhängigen, nicht metrischen (nominal- oder ordinalskalierten) Variablen (den Faktoren) untersucht.
Wir bezeichnen die abhängige Variable wieder mit X1, die Faktoren mit Großbuchstaben (A, B,..) und ihre Ausprägungen mit j,l, ...
Das Modell der mehrfaktoriellen Analyse lautet demnach:
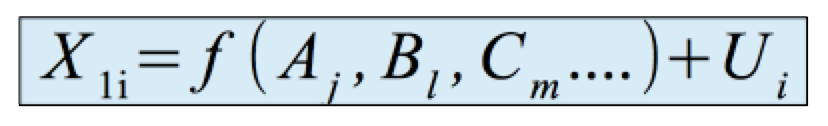 . .
b) Die Modellstruktur der mehrfaktoriellen Varianzanalyse
Die Struktur der mehrfaktoriellen Varianzanalyse lässt sich einfach am Beispiel der zweifaktoriellen Varianzanalyse verdeutlichen.
Die zweifaktorielle Analyse basiert auf den Faktoren:
 , ,
In Fortführung des einfaktoriellen Ansatzes
betrachten wir die Auswirkungen der nominal- bzw. ordinalskalierten Variablen Geschlecht und Ausbildungsniveau (mit drei Kategorien) auf die metrisch skalierte Variable Einkommen:
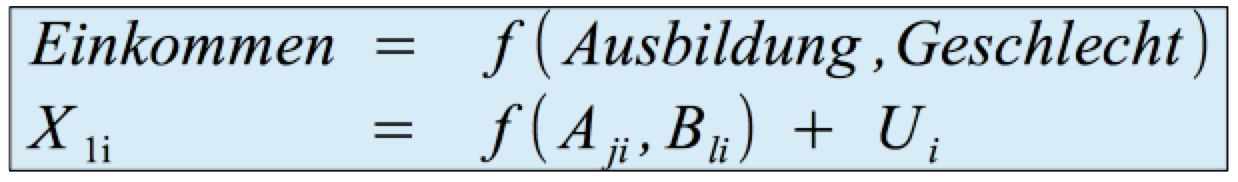 . .
Untersucht wird dabei die Abhängigkeit des Einkommens von der Ausbildung und dem Geschlecht mit der Vermutung, dass sich die Einkommensverteilungen der sechs, für die Faktoren zu bildenden Gruppen deutlich von einander unterscheiden.
c) Die tabellarische Darstellung des zweifaktoriellen Modellansatzes
-
In Tab. 12-5 sind die zellenspezifischen Einkommensverteilungen sowie die zugehörigen Mittelwerte und Summen der Abstandsquadrate tabellarisch festgehalten.
Tabelle 12-5: Die tabellarische Veranschaulichung der zweifaktoriellen Varianzanalyse
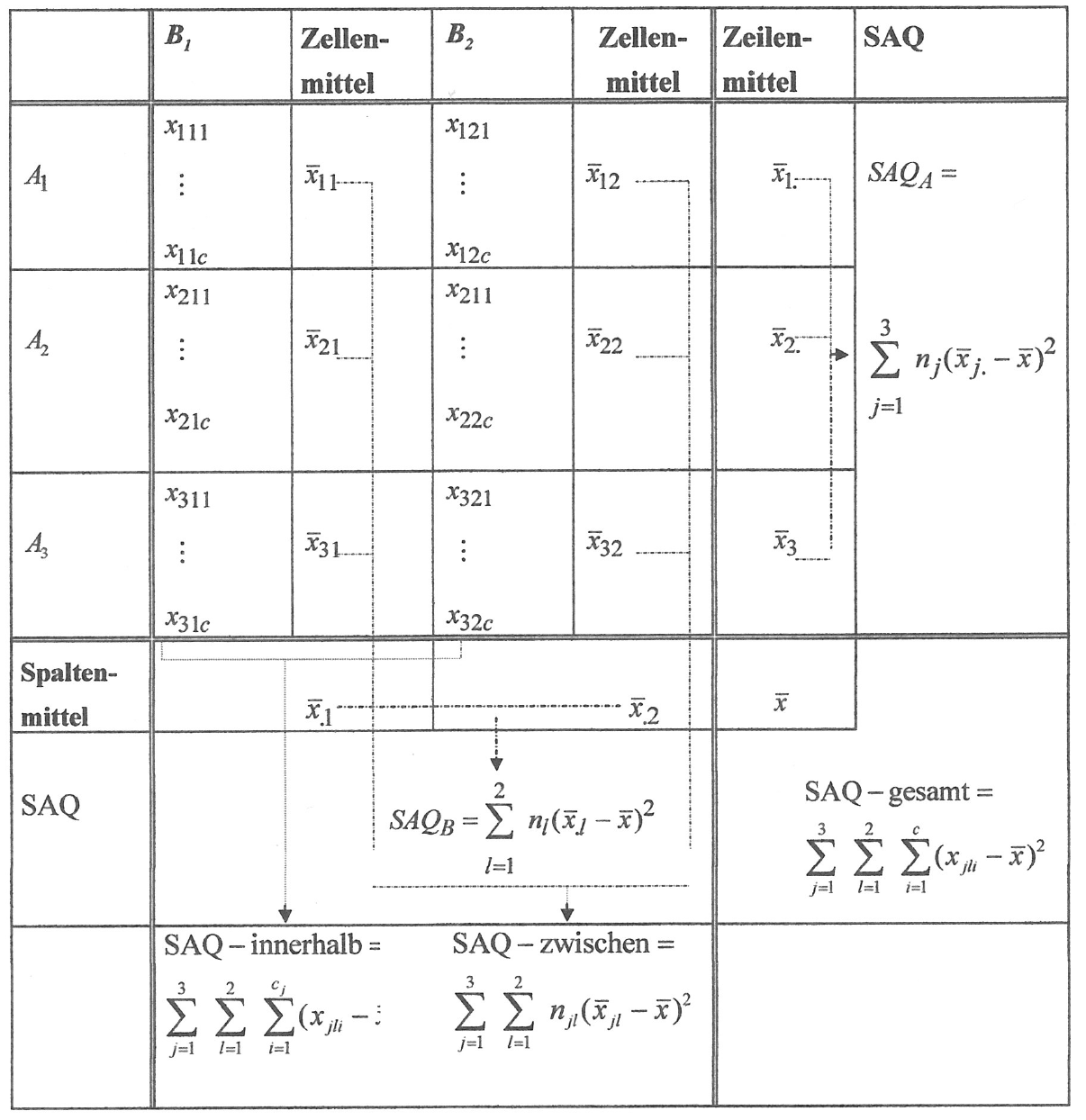
Die Interpretation der Tabelleninhalte
Das Schaubild präsentiert folgende statistische Angaben, aus denen die Komponenten des zweifaktoriellen, varianzanalytischen Modells abgeleitet werden:
In der Tabelle der Einkommensverteilung nach Ausbildungsgruppen und Geschlecht beinhalten die beiden ersten Spalten die Einkommensverteilungen und die Mittelwerte für das Geschlecht (z.B. "w") nach den Ausbildungskategorien.
-
In Spalte drei und vier werden die Einkommensverteilungen für das 2. Geschlechtsmerkmal (z.B. "m") wiedergegeben.
-
In Spalte fünf sind die Gruppen-Mittelwerte (empirische Randmittel) für die drei Ausbildungsgruppen ausgewiesen.
-
In der sechsten Spalte finden sich Angaben zur Streuung der Mittelwerte der Ausbildungs-Gruppen um das Gesamtmittel (SAQ-Haupteffekte des Faktors A).
-
In der vierten Zeile finden sich die Durchschnittseinkommen (empirische Randmittel) für die beiden Geschlechtergruppen.
-
In Zeile fünf sind die Streuung der der Mittelwerte der Geschlechts-Gruppen um das Gesamtmittel der Einkommen (SAQ-Haupteffekte des Faktors B) enthalten.
-
Die letzte Zeile komplettiert mit den Summen der Abstandsquadrate innerhalb der Zellen, der Abstandsquadrate der sechs Zellmittel zum Gesamtmittel (SAQ-zwischen) sowie der Gesamtsumme der Abstandsquadrate (SAQ-gesamt) die Verteilungs-Informationen.
d) Die Aussage der Modellkomponenten
Schaubild 12-5: Die Modellkomponenten der zweifaktoriellen Varianzanalyse
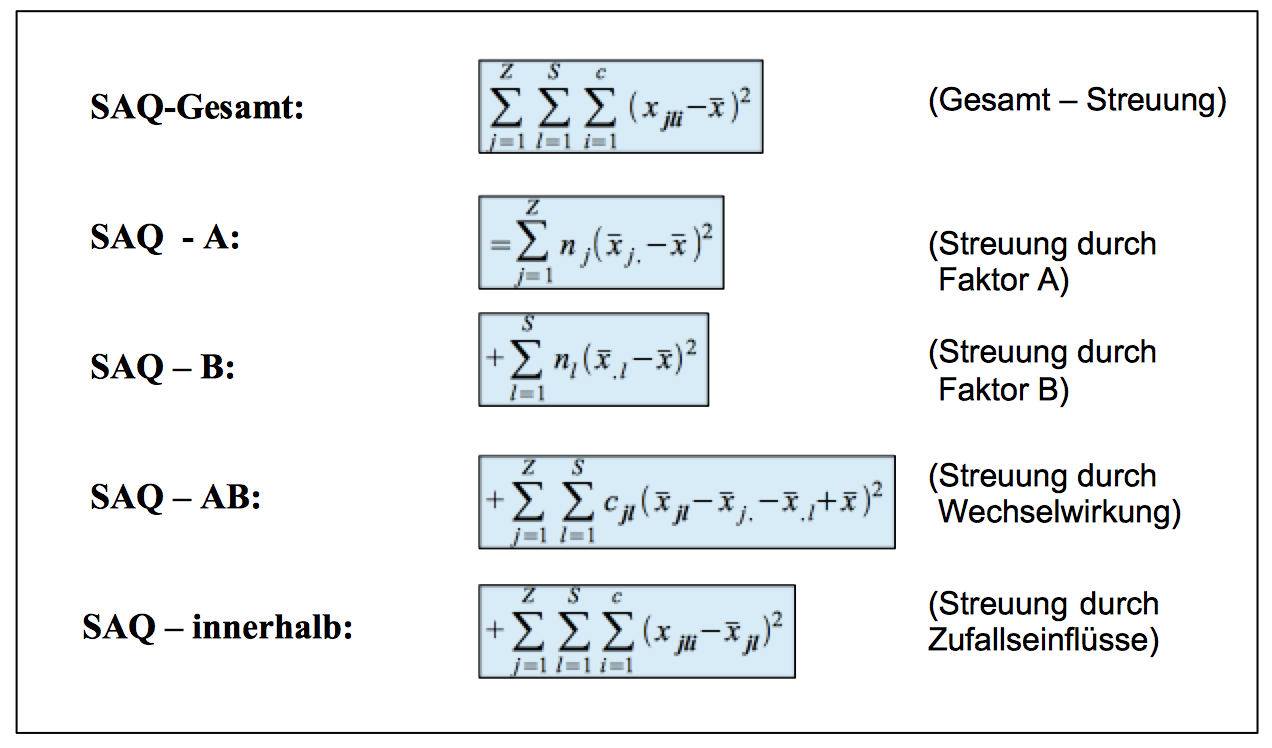
Die SAQ-gesamt: Die SAQ-gesamt drückt die Streuung der einzelnen Einkommen um das Durchschnittseinkommen aller Einkommensbezieher in Form des n-fachen Werts der Gesamtvarianz aus.
Die SAQ-zwischen: Diese SAQ erfasst die Streuung der Zellmittel um das Gesamtmittel und ist Ausdruck der faktor-bedingten Einkommensunterschiede. Diese beinhaltet:
die SAQ-Haupteffekte des Faktors A und damit die, der Ausbildung zuzuschreibenden Einflüsse auf das Einkommen,
die SAQ-Haupteffekte des Faktors B und damit die, dem Geschlecht zuzuschreibenden Auswirkungen sowie
die Wechselwirkung, die eine über-additive Wirkung beider Faktoren erfassen.
Die SAQ-innerhalb: Die SAQ-innerhalb erfasst die Einkommensunterschiede innerhalb der Zellen und damit die nicht faktor-abhängigen Einkommensunterschiede.
e) Die Zerlegung der Gesamt-Varianz
Die für die einfaktorielle Analyse gezeigte Aufteilung der Gesamtvarianz auf ihre Komponenten lässt sich in der mehrfaktoriellen Analyse nur im sog. experimentellen Ansatz, in dem alle Zellen gleich besetzt sind, additiv durchführen.
Unter dieser Voraussetzung gilt:
SAQ - gesamt = SAQ – zwischen (: SAQ-A + SAQ-B + SAQ-AB) + SAQ - innerhalb
Allerdings ist mit dem in Abschnitt 2. b) präsentierten Verfahren, Faktoren in Dummy-Variablen zu transformieren, eine Möglichkeit gegeben, Varianzanalysen als Regressionsanalysen durchzuführen.
Damit sind auch hierarchische Varianzanalysen möglich, die eine vollständige Aufteilung der SAQ - gesamt auf die partialisierten Modellkomponenten erlauben (vgl. dazu die im nächsten Modul im Abschnitt 1.c) durchgeführten Beispielsrechnungen).
f) Die Stärke des Zusammenhangs in der mehrfaktoriellen Varianzanalyse
2. Die klassische Kovarianzanalyse und das Allgemeine Lineare Modell (ALM)
a) Das Konzept der Kovarianzanalyse
-
Die Kovarianzanalyse verbindet eine Regressionsanalyse mit einer Varianzanalyse oder umgekehrt. Ihr Modellansatz formuliert den Zusammenhang:
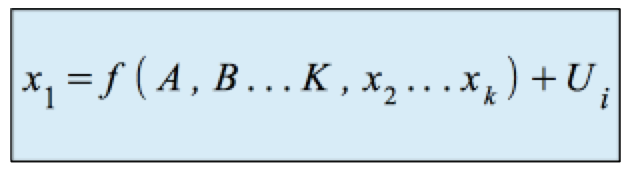
-
Wird die Varianzanalyse nach der Regressionsanalyse durchgeführt, werden die (metrischen) Fehler der abhängigen Variablen zusätzlich einer Varianzanalyse unterzogen:
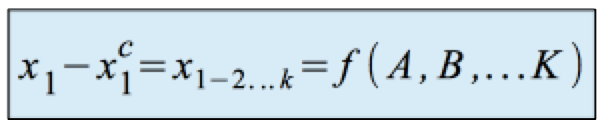
-
Dabei wird die SAQ-Res der Regressionsanalyse aufgespalten in einen Teil, der durch die Varianzanalyse weiter reduziert werden kann, und in einen Teil, der weder durch die Regressionsanalyse noch durch die Varianzanalyse erklärt werden kann:

-
Die Verbesserung der Erklärung der abhängigen Variablen wird durch das partielle eta-Quadrat ηK 2 gemessen:
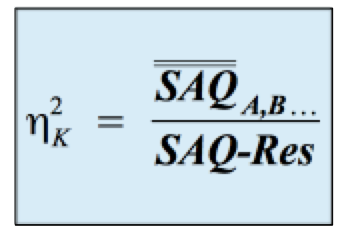
-
Wird die Regressionsanalyse nach der Varianzanalyse durchgeführt, werden die Fehler-SAQ der abhängigen Variablen in den Zellen zusätzlich mit einem Regressionsansatz analysiert:
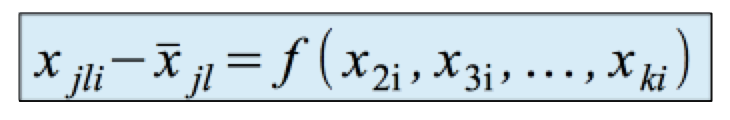
-
Dabei werden die SAQ-innerhalb aus der Varianzanalyse mit einer Regressionsanalyse weiter aufgespalten in einen Teil, der durch die die Regressionsanalyse weiter reduziert werden kann, und in einen Teil, der weder durch die Regressionsanalyse noch durch die Varianzanalyse erklärt werden kann:
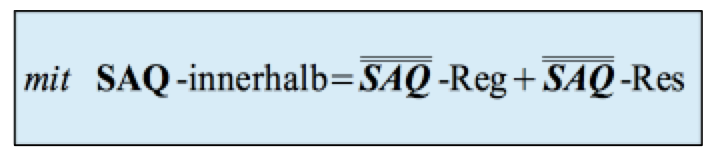
-
Die Verbesserung der Erklärung der abhängigen Variablen wird durch den partiellen Determinationskoeffizienten Rk 2 gemessen:
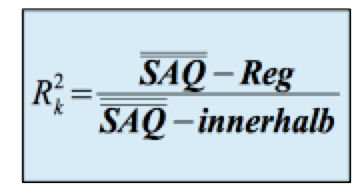
-
Beide Vorgehensweisen erbringen identische Verbesserungen der Erklärung und die jeweils nicht-erklärten Summen der Abstandsquadrate sind gleich:

b) Die Faktoren als Dummy-Variablen
In der klassischen Kovarianzanalyse ist es nicht möglich, die wechselseitige Abhängigkeit von Regressoren und Faktoren zu berücksichtigen. Deshalb ist ein Verfahren sinnvoll, die nichtmetrischen Faktoren in dichotome Variable umzuwandeln und diese danach in eine Regressionsanalyse zu integrieren.


c) Das Allgemeine Lineare Modell (ALM)
-
Im Allgemeinen Linearen Modell werden die Varianzanalyse und die Regressionsanalyse in einem konsistenten Modell zusammengeführt. Das ALM stellt somit die verallgemeinerte Form der Analyse eines linearen Zusammenhangs im Datensatz dar.
-
Dem Allgemeine Lineare Modell können also die Verfahren der einfachen und der multiplen Regressions- und Korrelationsanalyse wie die der Varianz-/Kovarianzanalyse zugeordneten werden.
-
Insbesondere wird dabei die Funktionsgleichung der Kovarianzanalyse:

in die Funktionsgleichung des Allgemeinen Linearen Modells transformiert:
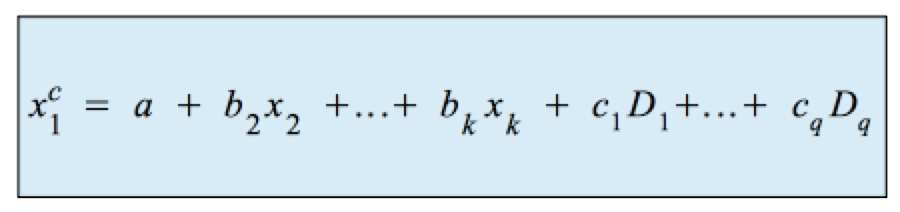
|



